
ЛАБ №4
.pdfЛабораторна робота №4 Просторові перетворення зображень
Мета: Метою даної лабораторної роботи є дослідження застосування апарату перетворення Фур’є для аналізу спектрів зображень та виконання фільтрації зображень у частотній області.
Подібно, як і для сигналів, для зображень існує множина лінійних перетворень, що значно розширюють можливості роботи з ними. Основними з них є - двовимірне дискретне перетворення Фур’є й дискретне косинусне перетворення.
1. Двовимірне дискретне перетворення Фур’є
Нехай f(x,y) = f(xi,yj) = fij; i= 0,1,2 3,…, M-1; j = 0,1,2,3, …, N-1 дискретне зображення, розміром MxN пікселів, i та j – номери пікселів по вертикалі й
горизонталі.
Тоді двовимірне дискретне перетворення Фур’є (двовимірне ДПФ, DFT – Discrete Fourier Transform) від цього зображення позначається, як F(ν,υ) = F(νk,υl) = Fkl і визначається в такий спосіб
M 1N 1
Fkl fij exp( j2 (ik / M jl / N)),
i 0 j 0
тут ν,υ – так звані просторові частоти, а k і l – номери частотних складових двовимірного дискретного перетворення Фур’є, k = 0,1,2,3,...,M-1; l = 0,1,2,3, …, N-1.
Просторові частоти ν,υ для двовимірної функції (зображення) мають той самий зміст, що й часова частота f для одномірної функції – сигналу.
Частота сигналу відображає швидкість зміни сигналу в часі, чим швидше змінюється сигнал, тим більш високі частоти присутні в його спектрі (у його перетворенні Фур’є).
Аналогічно, чим швидше змінюється зображення за відповідною координатою x або y, тим більш високі просторові частоти за цією координатою ν або υ має зображення.
Таким чином, двовимірне ДПФ переводить дискретне зображення з
області просторових змінних в область частотних змінних.
Відповідно, має місце й зворотне двовимірне дискретне перетворення Фур’є
M 1 N 1
fij 1/ MN Fkl exp( j2 (ik / M jl / N)),
k 0 l 0
яке переводить зображення із частотної області в область просторових змінних.
Тобто зображення можна представляти, як його відліками f(x,y) = f(xi,yj) = fij, у просторовій області, так і його спектральними коефіцієнтами F(ν,υ) =
F(νk,υl) = Fkl у частотній області.
2. Обчислення й відображення двовимірного ДПФ в MATLAB
Пряме й зворотне двовимірне дискретне перетворення Фур’є в MATLAB виконуються за допомогою алгоритму швидкого перетворення Фур’є (ШПФ, FFT
– Fast Fourier Transform), яке вимагає для свого виконання набагато менше операцій, ніж звичайне ДПФ.
Алгоритм двовимірного ДПФ масиву f розміром MxN в MATLAB реалізується функцією
F = fft2(f)
Ця функція повертає в якості результату також двовимірний масив, але вже коефіцієнтів ДПФ розміром MxN, початок масиву перебуває у верхньому лівому куті й має координати (1,1).
Перетворення Фур’є має комплексний вигляд, тобто F = Re(F) + jim(F). Тому, для його відображення, якщо це потрібно, необхідно знайти модуль спектра - корінь квадратний із суми квадратів дійсної й уявної
компонент – S=abs(F).
Відображення спектра, так само, як і вихідного зображення, здійснюється
з використанням функції
imshow(S, []).
Приклад:
clear; close all;
f = imread('cameraman.tif'); imshow(f); title('Зображення');
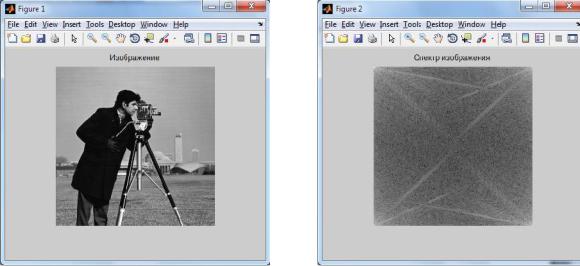
F = fft2(f); S=abs(F); Slog=log(1+S); figure imshow(Slog, [ ]);
title('Спектр зображення');

У цьому прикладі замість модуля спектра відображаються його логарифм, оскільки масштаб отриманих у результаті ДПФ чисел значно відрізняється від масштабу самого зображення.
Іноді зручніше відображати спектр зображення з початком не в точках (1,1), а в центрі частотної області (в центрі прямокутника MxN). Для цього використовується функція fftshift.
Приклад:
f = imread('cameraman.tif'); imshow(f); title('Зображення');
F = fft2(f);
S=abs(F);
Fc= fftshift(S); Slog=log(1+Fc); figure imshow(Slog, []);
title('Спектр зображення');
За допомогою команди F = fftshift(Fc) можна повернути спектр до початкового вигляду (з нумерацією від нульової точки у верхньому лівому куті).
Відновлення зображення за його спектром здійснюється з використанням функції
Приклад:
f = imread('moon.tif'); imshow(f);
title('Зображення'); F = fft2(f);
Fc = fftshift(F); Fdc = ifftshift(Fc); If = ifft2(Fdc); figure
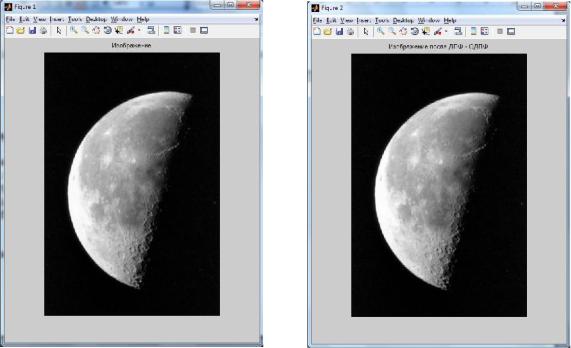
imshow(If, []);
title('Зображення після ДПФ - ОДПФ');
3. Фільтрація зображень у частотній області
Основою фільтрації зображень у частотній і просторовій області є теорема про згортку, яку можна записати таким чином:
h(x,y)f(x,y) ↔ H(ν, υ) F(ν, υ),
і у зворотний бік
h(x,y) f(x,y) ↔ H(ν, υ)F(ν, υ).
Головне в цих виразах це те, що згортку двох двовимірних функцій можна одержати як ОДПФ від добутку їх спектрів. Одним із цих спектрів є спектр зображення. Другим – перетворення Фур’є від вікна фільтра.
Навіщо й чому це робиться?
Оскільки згортка – це основна операція фільтрації сигналів і зображень, то дуже важливо знати, скільки дій потрібно виконати, щоб профільтрувати сигнал або зображення.
Відомо, що для виконання дискретної згортки двох сигналів розміром N відліків кожний відповідно до формули
m
yi xi k hk k 0
потрібно приблизно N2 операцій множення.
Відповідно, для фільтрації зображення, розміром NxN пікселів двовимірним фільтром розміром MxM точок, відповідно до формули
yij xi k , j l hkl
k l
потрібно виконати порядку N2M2 операцій множення. При великих розмірах зображень N2 і великих розмірах вікна фільтра M2 кількість дій отримується занадто велика.
Згортці зображень у просторовій області відповідає добуток у частотній області.
Але під час множення двох масивів кількість операцій дорівнює розміру масивів, що перемножуються, то абсолютно очевидний великий виграш у кількості операцій, якщо фільтрацію виконувати саме в частотній області.
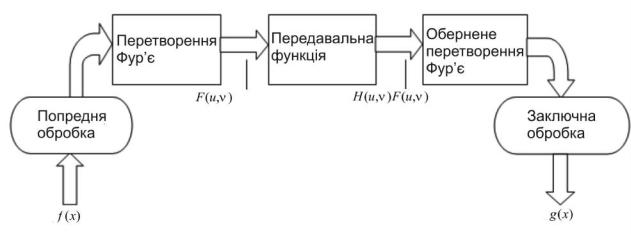
Процедура фільтрації в цьому випадку здійснюється в такий спосіб:
Фільтрація в цьому випадку складається з декількох етапів:
- зображення переводиться в частотну область шляхом виконання над ним двовимірного дискретного перетворення Фур’є:
f → F
- передавальна функція фільтра також переводиться в частотну область, у результаті отримаємо двовимірну частотну характеристику фільтра:
h → H
- спектр зображення множиться на частотну характеристику фільтра, у результаті отримаємо спектр зображення на виході фільтра:
Y = H F
- над спектром Y виконується зворотне перетворення Фур’є, у результаті отримаємо відфільтроване зображення y.
Незважаючи на уявну складність процедури фільтрації в частотній області, кількість операцій ЕОМ, яка необхідна для її виконання, на кілька порядків менше, чим під час виконання прямої згортки. Для цього потрібно лише вміти виконувати процедуру двовимірного дискретного перетворення Фур’є.
Розглянемо, як отримують, і як виглядають частотні характеристики двовимірних фільтрів.
3.1. Частотні характеристики двовимірних фільтрів
Як приклад розглянемо двовимірний фільтр нижніх частот (ФНЧ) з
гаусівською формою вікна фільтра, і параметрами:
h = fspecial('gaussian', [200 200], sigma);
Приклад:
clear; close all; sigma = 1;
h = fspecial('gaussian', [200 200], sigma); imshow(250*h),
title('Вікно фільтра') H = fft2(h); SH=abs(H);
Shc= fftshift(SH); Shlog=log(1+Shc); figure imshow(Shlog, []);
title('Частотна характеристика фільтра');
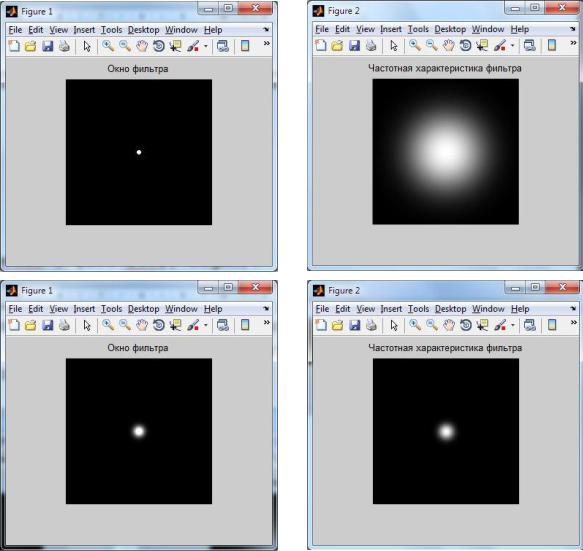
На рисунках наведений вигляд вікна фільтра (лівий малюнок) і його частотної характеристики (правий малюнок) для двох значень параметра фільтра sigma = 1 і sigma = 5. Параметр sigma визначає фактичний розмір вікна фільтра, чим більше sigma, тим більше вікно фільтра.
Розмір вікна фільтра (малюнки ліворуч) визначає, скільки точок зображення потрапляє в це вікно в процесі фільтрації. Або інакше кажучи, за скількома точками вихідного зображення формується одна точка на виході фільтра.
З малюнків видно, що чим менше розмір вікна фільтра, тем повільніше спадає частотна характеристика фільтра по мірі віддалення від центру, тобто тим більш це широкосмуговий фільтр. Якщо ж розмір вікна фільтра великий, то частотна характеристика убуває дуже швидко при віддаленні від центру вікна (від нуля). Тобто фільтр стає більш вузькополосним.
3.2. Процедура фільтрації
Процедура фільтрації в частотній області, як ми вже говорили, полягає в множенні спектра фільтрованого зображення на частотну характеристику фільтра, і виконання ОДПФ від результату. Але для поелементного множення двох масивів потрібно, щоб розміри цих масивів були однаковими.
Відомо, також, що під час виконання ШПФ (FFT) розмір масиву спектру, що отримується (у тому числі – і при двовимірному перетворенні) збігається з розміром масиву, від якого здійснюється ДПФ. Тобто, якщо нам потрібно, щоб розмір масиву частотної характеристики збігався з розміром масиву спектра зображення, потрібно, щоб розмір вікна фільтра збігався з розміром зображення.
В MATLAB є спеціальні функції, які дозволяють збільшувати розміри будь-яких масивів шляхом додавання потрібної кількості нулів до вихідного масиву. Але можна зробити ще простіше. Відразу ж скористатися фільтром, розмір вікна якого (задається в параметрах фільтра) збігається з розміром зображення.
Наприклад, розмір зображення 'cameraman.tif' складає 256х256
пікселів. Отже, у параметрах h = fspecial('gaussian', [200 200],
sigma); можна визначити розмір вікна [256 256].
Приклад:
clear; close all;
f = imread('cameraman.tif'); imshow(f);
title('Вихідне зображення'); F = fft2(f);
S=abs(F);
Fc= fftshift(S); Slog=log(1+Fc); figure imshow(Slog, []);
title('Спектр вихідного зображення'); sigma=1;
h = fspecial('gaussian', [256 256], sigma); figure
imshow(250*h), title('Вікно фільтра') H = fft2(h);
SH=abs(H);
Shc= fftshift(SH); Shlog=log(1+Shc); figure imshow(Shlog, []);
title('Частотна характеристика фільтра'); IF=F.*H;
SIF=abs(IF);
Sifc= fftshift(SIF); Sifclog=log(1+Sifc); figure imshow(Sifclog, [ ]);
title('Спектр на виході фільтра'); FI = ifft2(IF);
Fiabs=abs(FI);
Fiabsc= fftshift(Fiabs); Filog=log(1+Fiabsc); figure
imshow(Filog, []);
title('Зображення на виході фільтра');
Завдання на самостійну роботу
1.Завантажте з бібліотеки MATLAB кілька різних зображень.
2.З використанням функції F = fft2(f) сформуйте й відобразіть двовимірні спектри зображень. При відображенні спектра використовуйте або логарифмічний масштаб, або підберіть масштаб уручну шляхом ділення значень спектра на деяку константу. Можна, також, пронормувати значення спектра до максимального, а потім домножити кожне значення на 255 (максимальна яскравість для uint8).
3.З використанням функції fftshift приведіть нульову частоту в спектрі до центру вікна відображення.
4.З використанням функції ifft2(F) відновіть зображення за його
спектром (використовуйте спектри з нульовою частотою у верхньому лівому куті й з нульовою частотою в центрі вікна). Поясніть отримані в обох випадках результати.
5. З використанням функції fspecial('gaussian') задайте двовимірний фільтр із параметрами [M N], sigma в області просторових змінних. Відобразіть у вигляді зображення вигляд вікна цього фільтра.
6.Визначте вигляд частотної характеристики даного фільтра. Відобразіть АЧХ двовимірного фільтра у вигляді зображення – imshow.
7.Змініть параметр sigma фільтра, і повторіть п.п. 5,6. Поясніть відмінності в отриманих результатах.
8.Виконайте фільтрацію зображень у частотній області з використанням фільтрів згідно п.п. 5, 6, 7. Поясніть відмінності в отриманих результатах.
9.З використанням того самого віконного фільтра, заданого функцією fspecial('gaussian'), виконайте фільтрацію зображення в області
просторових змінних. Порівняйте результат з п.8.
