18.3. Розрахунок сталих Стефана - Больцмана та Віна за допомогою формули Планка

1. Стала Стефана-Больцмана. Повернувшись до змінної , запишемо енергетичну світність АЧТ у вигляді

. (1)

Інтеграл у (1) обчислюється аналітично і він дорівнює

. (2)

Підставляючи (2) у (1), одержимо

. (3)

П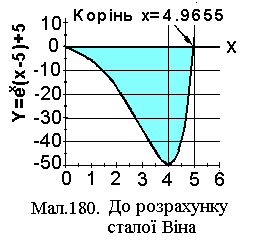орівнюючи (3) із формулою Стефана-Больцмана, знайдемо сталу Стефана-Больцмана

. (4)

2. Стала Віна. Уведемо змінну х у такий спосіб

Універсальна функція Кірхгофа може бути представлена як функція

.

Уведемо у (4) змінну х

(5)

Для визначення положення екстремуму в (5) знайдемо похідну і прирівняємо її до 0

. (6)

Р о з в' я з о к (6) зводиться до розв’язку трансцендентного рівняння

. (7)

Дійсно, прямі розрахунки дають

Рівнянню (7) задовольняють значення , які відповідають мінімумам функції, а значення х, що відповідає максимумуможна знайти, розв’язавши рівняння (7) графічно. Такий розв'язок (див. ) даєі тому

.

Порівнюючи одержаний вираз із законом зміщення Віна, знаходимо, що стала Віна дорівнює

. (8)

18.4. Оптична пірометрія

Пірометрія ­­­­­­­сукупність оптичних методів вимірювання температури за інтенсивністю теплового випромінювання тіл. Прилади, за допомогою яких проводиться таке вимірювання, називаються пірометрами. В оптичній пірометрії застосовуються методи, в основі яких лежать вимірювання за енергетичною світністюR, випромінювальною здатністюта спектральним розподілом енергії випромінювання тіл. У зв’язку з цим розрізнюють три види пірометричної температури тіл, через які розраховується звичайна температура тіла.

1. Радіаційна температура. Радіаційна температура T_рад тіла ­­­­ це температура АЧТ, при якій, його енергетична світність R^* дорівнює енергетичній світності тіла R. Порівнювання проводиться термостовпчиком, підключеним до гальванометра, на який фокусується поверхня тіла, що досліджується. Прилад градуюють по АЧТ. Згідно закону Больцмана

,(1)

і при рівності R^*=R одержимо

, (2)

де ­­­­ коефіцієнт сірості тіла. Наприклад, при істинній температурі вольфраму 3000 К його Т_рад = 2250 К.

2. Яскравісна температура: Яскравісна температура тіла T_яс ­­­­ це температура АЧТ, при якій, його випромінювальна здатність дорівнює випромінювальній здатності тіла. Порівнювання проводиться яскравісним пірометром із зникаючою ниткою. Пірометр має відградуйовану лампочку. Нитка лампочки лежить у площинідо осі приладу. В цю ж площину через світлофільтр із=660 нм фокусується поверхня тіла, що досліджується. Змінюючи реостатом напругу, яка живить лампочку, доводять її яскравість до яскравості тіла і в цю мить зображення нитки зникає на фоні поверхні тіла. Істинне значення температури обчислюється за формулою

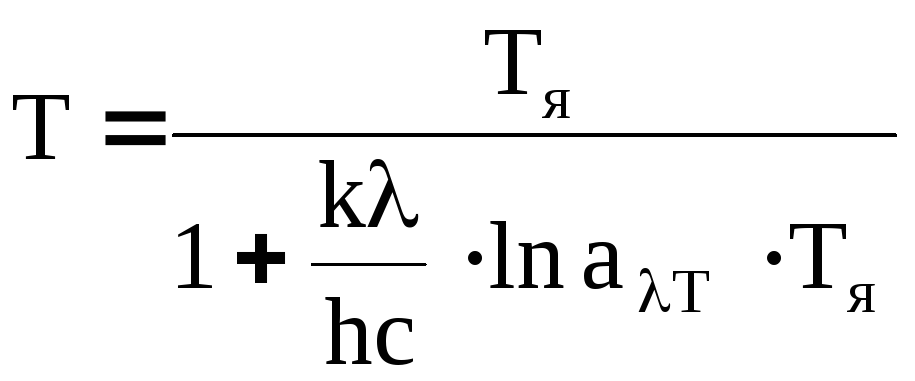, (3)

де k ­­­­ стала Больцмана, ­­­­ поглинальна здатність тіла. З формули (3) видно, що при істинна температура Т>T_яскр. Значення можна знайти з таблиць. Наприклад, для вольфраму при Т=3000 К і=660 нм=0.46. Обчислення за формулою (3) дає Т_яскр=2700 К.

Формулу (3) можна одержати у такий спосіб. За визначенням яскравісної температури випромінювальні здатності тіла і АЧТ рівні, тобто

. (4)

У видимому світлі завжди

, (5)

а тому, використовуючи формулу Планка, з (4) одержимо

. (6)

Після логарифмування (6) маємо

(7)

і, розв'язуючи (6), одержимо (3).

Для практичної роботи, вважаючи, що , із (7)

можна одержати вираз для

. (8)

Тепер перерахунок яскравісної температури у температуру тіла для яскравісного пірометра проводиться за формулою

. (9)

Для кожного з пірометрів величина знаходиться знаходиться за методом найменших квадратів і указується на лабораторному стенді.

3. Кольорова температура. Для будь-якого тіла випромінювальна здатність може бути представленна через поглинальну здатністьі випромінювальну здатність АЧТу виді

У випадку сірого тіла

і тоді спектри випромінювання тіла й АЧТ будуть подібні. При цьому положення максимуму спектра випромінювання АЧТ співпадає з положенням максимуму випромінювання тілай температура тіла може бути знайдена із закону зміщення Віна

.

Максимум спектра випромінювання Сонця за атмосферою Землі лежить на _m=480 нм і після проходження атмосфери він зміщується до _m=550 нм. За формулою Віна Т_кол=b/_m=6000K, а розрахунки радіаційної температури дають Т_рад=5800 К. Близькі значення указують на те, що поверхня Сонця за своїми властивостями близька до поверхні АЧТ.