7.8. Перший закон (начало) термодинаміки

Перший закон (начало) термодинаміки  передане системі тепло , створює приріст внутрішньої енергії системи dU та йде на виконання нею елементарної роботи

(нагадаємо, що символом позначаються елементарні величини, які не є функціями стану системи).

Перший закон термодинаміки виражає загальний закон збереження та перетворення енергії і не визначає напрямок протікання процесу теплопередачі, а також умов, за яких відбувається теплопередача. Це питання врегульовується другим законом термодинаміки.

7.9. Адіабатичний процес

Адіабатичним називається термодинамічний процес, що переводить термодинамічну систему в різні рівноважні стани без теплообміну із зовнішнім середовищем, тобто коли Q=0. Для ідеального газу справджується рівняння адіабати

, (1)

де  = стала адіабати, що залежить від структури складових газу. Разом із тим рівноважні стани описуються одночасно і рівнянням Клапейрона - Менделєєва .

Щоб одержати рівняння (1), запишемо перший закон термодинаміки у вигляді

. (2)

Узявши диференціал по P,V,T у рівнянні стану , матимемо

, (3)

і після підстановки в перший закон термодинаміки одержимо

. (4)

Поділивши ліву частину (4) на PV, одержимо

,

що й треба було довести.

Користуючись об'єднаним газовим законом , одержане рівняння адіабати можна записати в таких видах

, . (5)

Робота розширення газу від до при адіабатичному процесі може бути одержана з першого начала Q=dU+A=0, а саме

A=-dU. (6)

В інших виразах роботу можна знайти прямим обчисленням

. (7)

Таблиця 3. Характеристики ізопроцесів.

Назва процесу	Рівняння процесу	Зв'язок між параметрами стану	Робота в процесі	Тепло, передане в процесі
Ізохорний	V = const		A = 0, A = 0	Q = CVdT, Q=CV(T2 - T1)
Ізобарний	Р = const		A = РdV, A = Р(V2 - V1)	Q = CpdT, Q=Cp(T2 - T1)
Ізотермічний	T = const	РV = const	A = РdV, A = RTln(), A = RTln(),	Q = A, Q = A
Адіабатний	Q = 0	PV  = const TV(- 1)=const	A = pdV = - dU A = - U = CV(T1 - T2)	Q = 0, Q = 0

7.10. Теплоємність ідеального газу

Теплоємністю С термодинамічної системи називається відношення елементарного тепла , переданого системі, до відповідної величини зміни температури тіла dT

(1)

(2)

і вона чисельно дорівнює теплоті, необхідній для збільшення температури тіла на 1К. Питома теплоємність с  теплоємність одиниці маси речовини с = С/m, а молярна .

Теплоємність при сталому об'ємі позначається як (система не виконує роботи pdV=0) і може бути обчислена з (2)

. (3)

Внутрішню енергію газу можна записати через

. (4)

Теплоємність при сталому тискові позначається як і може бути обчислена з (2) при врахуванні (3) так

.

Ми знайшли d(pV) із рівняння Клапейрона-Менделєєва, врахувавши, що P=const,

Знайдемо відношення до

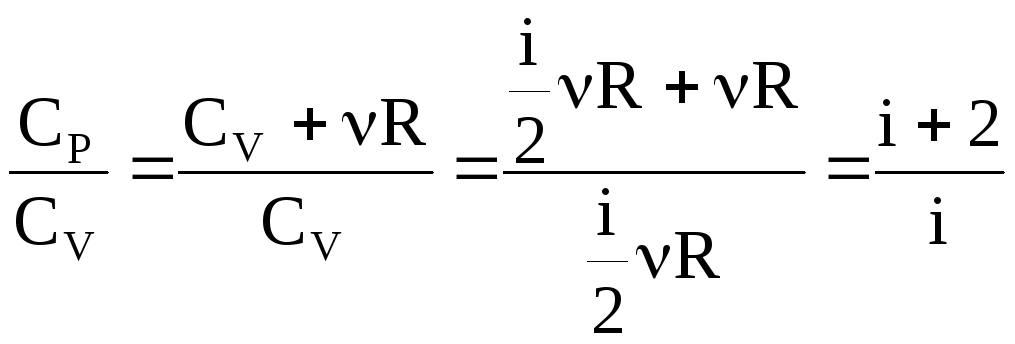. (5)

З (5) видно, що стала адіабати може бути представлена через відношення теплоємностей при сталому тискові і при сталому об'ємі так

.