7.5. Ідеальний газ. Термодинамічні процеси в ідеальному газі

Ізотермічний процес ідеального газу  процес, що переводить термодинамічну систему в різні рівноважні стани при сталій температурі й зв'язок між термодинамічними параметрами описується законом Бойля - Маріотта

,

де тиск і об'єм газу після і-го ізотермічного процесу.

Ізобаричний процес ідеального газу  процес, що переводить термодинамічну систему в різні рівноважні стани при сталому тискові й зв'язок між термодинамічними параметрами описується законом Шарля

,

де температура і об'єм газу після і-го ізобаричного процесу.

Ізохоричний процес ідеального газу  процес, що переводить термодинамічну систему в різні рівноважні стани при сталому об'ємі й зв'язок між термодинамічними параметрами описується законом Гей-Люсака

,

де температура і тиск газу після і-го ізохоричного процесу.

Об’єднаний газовий закон  при будь-яких переходах ідеального газу з одного рівноважного стану в інший рівноважний стан виконується співвідношення виду

,

де температура і об'єм газу після і-го будь-якого процесу.

Закон Авогадро: при однакових тисках і температурах у рівних об'ємах різних ідеальних газів міститься однакове число молекул або теж саме: при однакових тисках і температурах моль різних ідеальних газів займає однаковий об'єм. За нормальних умов (t) моль будь-яких ідеальних газів займає об'єм.

Рівняння стану ідеального газу описується рівнянням Клапейрона - Менделєєва

,

де маса газу, його молярна маса, акількість молів газу, R = 8. 31 Дж/(моль К) - універсальна газова стала.

З рівняння Клапейрона - Менделєєва PV = RT витікає рівняння для тиску, яке співпадає з рівнянням, обчисленим в молекулярно-кінетичній теорії,

де маса молекули, n=N/V - концентрація частинок.

Парціальний тиск газу в суміші - тиск, який мав би цей газ, якщо б із суміші були вилучені всі інші гази, а об'єм і температура залишились би попередніми.

Закон Дальтона: тиск суміші з N ідеальних газів дорівнює сумі їх парціальних тисків

.

У випадку реальних газів існує декілька рівнянь стану, які описують його певну фізичну модель, наприклад, рівняння Ван-дер-Ваальса.

7.6. Поняття внутрішньої енергії

Внутрішня енергія U термодинамічної системи є сума:

а) кінетичної енергії хаотичного теплового руху частинок системи (молекул, атомів, іонів, вільних електронів і т. п. ),

б) потенційної енергії взаємодії цих частинок,

в) енергії взаємодії атомів чи іонів у молекулі,

г) енергії атомів та іонів,

д) енергії ядер,

е) енергії електромагнітного випромінювання.

Внутрішня енергія є однозначною функцією стану системи: її приріст U при переході зі стану І в стан ІІ не залежить від виду процесу і дорівнює U = U₂ - U₁. У випадку кругового процесу повна зміна внутрішньої енергії системи дорівнює нулю.

В елементарній термодинаміці ідеального газу внутрішня енергія включає лише кінетичну енергію хаотичного теплового руху частинок системи.

7.7. Робота термодинамічної системи

Умовою здійснення термодинамічною системою елементарної роботи А є переміщення взаємодіючих із нею зовнішніх тіл. При цьому елементарна робота А' зовнішніх тіл над системою А' = - А.

Роботою розширення газу називається робота, що здійснюється системою проти сил зовнішнього тиску. При цьому елементарна робота дорівнює

А = PdV і .

Наприклад, при розширенні газу в циліндрі (див. Мал. 12), газ створює тиск Р на поршень площею S і в результаті на нього діє сила F = PS. При переміщенні поршня на dx, газ виконує роботу

,

де dV - приріст об'єму газу.

Робота розширення газу від об'єму V₁ до об'єму V₂ при ізотермічному процесі () дорівнює A=. З рівняння Клапейрона - Менделєєва маємо

,

Робота розширення газу від V₁ до V₂ при ізобаричному процесі ()

.
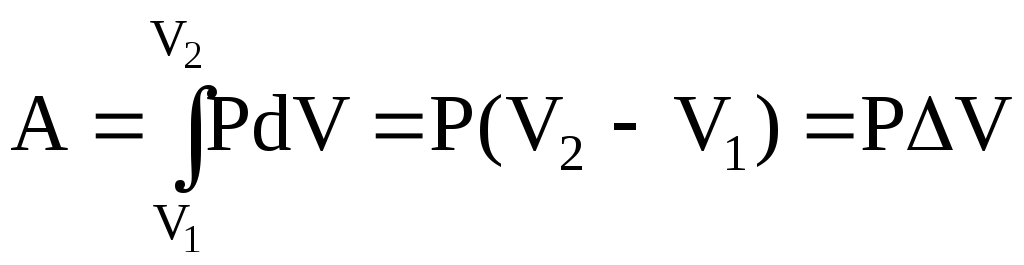