
2. Методи пошуку мінімуму для унімодальних функцій
Метод дихотомії
Найпростішим наближеним методом, який використовує лише інформацію про значення цільової функції в точках допустимої множини є метод поділу відрізка навпіл (або метод дихотомії).
Нехай
функція
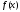 унімодальна на відрізку
унімодальна на відрізку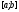 .
.
У процесі роботи методу дихотомії будується послідовність вкладених відрізків
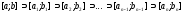 ,
,
кожен
з яких містить хоча б одну точку мінімуму
 функції
функції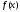 на
на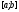 .
.
Нехай
задані числа
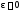 (необхідна точність визначення точки
(необхідна точність визначення точки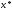 )
і
)
і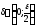 .
.
Пошук
точки мінімуму функції
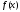 на відрізку
на відрізку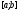 починається з вибору двох точок
починається з вибору двох точок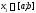 ,
,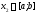 за правилом:
за правилом:
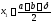 ,
,
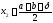 .
.
Точки
 розміщені симетрично відносно середини
відрізка
розміщені симетрично відносно середини
відрізка і при малих
і при малих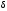 ділять відрізок майже навпіл (звідси
назва методу).
ділять відрізок майже навпіл (звідси
назва методу).
Перехід
від відрізка
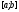 до відрізка
до відрізка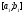 відбувається так:
відбувається так:
якщо
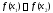 ,
то покладають
,
то покладають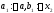 (рис. 5 а), в протилежному випадку
(рис. 5 а), в протилежному випадку (рис. 5 б).
(рис. 5 б).
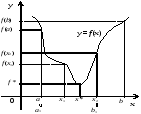
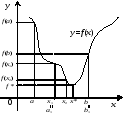
а) б)
Рис. 5.
В
силу унімодальності функції
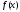 на відрізку
на відрізку зрозуміло, що відрізок
зрозуміло, що відрізок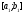 має хоча б одну спільну точку з множиною
має хоча б одну спільну точку з множиною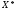 точок мінімуму функції
точок мінімуму функції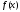 на
на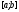 (рис. 5, 6) і його довжина дорівнює
(рис. 5, 6) і його довжина дорівнює
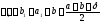 або
або
 і
і
Для
зручності подальших обрахунків для
визначення
 будемо використовувати співвідношення
будемо використовувати співвідношення
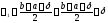 . (2)
. (2)
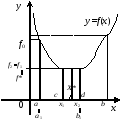
Рис. 6.
Нехай
вже отриманий відрізок
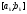 такий, що
такий, що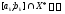 ,
при цьому, з урахуванням (2), його довжина
дорівнює
,
при цьому, з урахуванням (2), його довжина
дорівнює
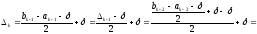
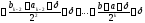 .
.
Отже,
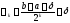 . (3)
. (3)
Якщо
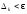 ,
то задача розв'язана із заданою точністю
,
то задача розв'язана із заданою точністю і за наближення до деякої точки
і за наближення до деякої точки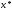 множини
множини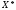 можна взяти точку
можна взяти точку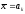 ,
якщо
,
якщо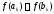 ,
або
,
або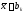 ,
якщо
,
якщо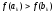 ,
а значення
,
а значення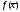 буде наближенням для
буде наближенням для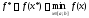 .
.
Зауваження.
На практиці часто за наближення точки
мінімуму функції
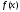 на
на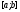 приймають точку
приймають точку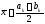 з меншою ніж в попередньому випадку
похибкою:
з меншою ніж в попередньому випадку
похибкою:
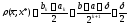 .
.
Якщо
ж величина
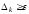 ,
то визначаються точки
,
то визначаються точки
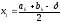 ,
,
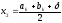 .
.
і
обчислюються значення
 і
і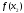 .
.
Якщо
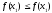 ,
то покладають
,
то покладають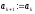 ,
,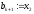 ,
інакше
,
інакше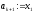 ,
,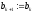 .
.
Згідно
з (3), довжина отриманого відрізка
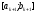 дорівнює
дорівнює
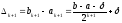
і
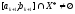 .
Після чого повторюється перевірка умови
.
Після чого повторюється перевірка умови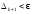 і т.д.
і т.д.
Розглянемо
алгоритм, який реалізує описаний метод
дихотомії і, також, визначає кількість
зроблених ітерацій
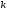 для досягненні точності
для досягненні точності і кількість обчислень значень цільової
функції
і кількість обчислень значень цільової
функції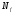 .
Параметри
.
Параметри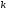 і
і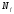 на практиці використовуються для
контролю кількості можливих обчислень
значень функції, а також для порівняння
з іншими методами.
на практиці використовуються для
контролю кількості можливих обчислень
значень функції, а також для порівняння
з іншими методами.
Алгоритм 2.
(методу дихотомії)
Нехай
задано
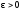 ,
,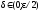 і відрізок
і відрізок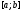 ,
де функція
,
де функція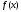 унімодальна. Покласти
унімодальна. Покласти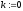 .
.
Крок 1. Знайти точки
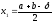 ,
,
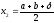
і
обчислити
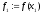 ,
,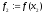 .
.
Крок 2.
Якщо
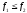 ,
то покласти
,
то покласти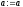 ,
,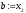 ,
,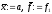 інакше
інакше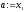 ,
,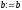 ,
, .
.
Крок 3.
Якщо
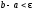 ,
то покласти
,
то покласти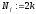 і перейти на крок 4, в протилежному
випадку покласти
і перейти на крок 4, в протилежному
випадку покласти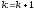 і перейти до виконання кроку 1.
і перейти до виконання кроку 1.
Крок 4.
Вивести
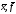 ,
,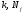 .
Кінець алгоритму.
.
Кінець алгоритму.
Оскільки
кожен крок методу вимагає обчислення
значення функції
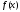 у двох точках, то для досягнення потрібної
точності
у двох точках, то для досягнення потрібної
точності необхідно зробити
необхідно зробити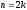 обчислень значень функції, при цьому з
(3) маємо
обчислень значень функції, при цьому з
(3) маємо
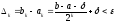 . (4)
. (4)
Звідси випливає, що число кроків алгоритму задовольняє умову
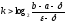 .
.
Часто
на практиці число
 можливих обчислень значень функції
можливих обчислень значень функції задане заздалегідь і його перебільшення
небажане.
задане заздалегідь і його перебільшення
небажане.
В
цьому випадку нерівність (4) дає можливість
оцінити точність отриманого наближення
 після
після обчислень значень функції:
обчислень значень функції:
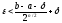 .
.
Примітки:
1.
Величина
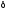 в методі дихотомії вибирається в
залежності від кількості ймовірних
десяткових знаків при обчисленні
аргументу
в методі дихотомії вибирається в
залежності від кількості ймовірних
десяткових знаків при обчисленні
аргументу і не може бути меншою за машинний нуль
конкретної ЕОМ, яка використовується
при розв'язуванні задачі.
і не може бути меншою за машинний нуль
конкретної ЕОМ, яка використовується
при розв'язуванні задачі.
2.
Метод дихотомії без змін можна застосувати
для мінімізації функцій, які не є
унімодальними. Однак у цьому випадку
не можна гарантувати, що отриманий
розв'язок буде досить хорошим наближенням
до точки глобального мінімуму функції
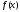 .
.
Метод золотого перерізу
Розглянемо метод мінімізації унімодальної функції на заданому відрізку, який за своєю структурою є досить простим і дозволяє розв'язати задачу з необхідною точністю при меншій кількості обчислень значень функції порівняно з методом дихотомії.
В основу цього методу покладено властивості золотого перерізу відрізка.
Поділ відрізка на дві нерівні частини так, що відношення довжини всього відрізка до довжини його більшої частини дорівнює відношенню довжини більшої частини до довжини меншої частини відрізка називається золотим перерізом цього відрізка.
Визначимо
точки, якi здійснюють золотий переріз
заданого відрізка
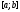 .
.
Очевидно, що таких точок буде дві (рис. 7. а).
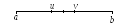
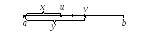
a) б)
Рис. 7.
Згідно
означення золотого перерізу, можна
скласти два рівняння відносно невідомих
 i
i відповідно :
відповідно :
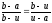 (5)
(5)
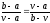 (6)
(6)
Розв'язок рівнянь (5) i (6) будемо шукати у вигляді:
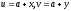 ,
,
де
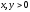 і
і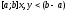 (рис. 7. б).
(рис. 7. б).
Одержуємо два квадратних рівняння
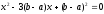 ,
,
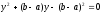 ,
,
коренями яких є
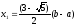 і
і
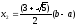 ,
,
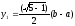 і
і
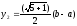 .
.
Оскільки
для точок
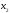 i
i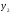
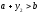 i, то золоті перерізи визначаються
точками
i, то золоті перерізи визначаються
точками
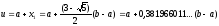 , (7)
, (7)
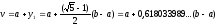 . (8)
. (8)
Ці
точки розташовані симетрично відносно
середини відрізка
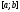 i
i ,
при цьому шукане відношення між довжинами
відрізків у золотому перерізі, наприклад,
з (5) і (7) дорівнює
,
при цьому шукане відношення між довжинами
відрізків у золотому перерізі, наприклад,
з (5) і (7) дорівнює
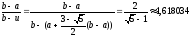 . (9)
. (9)
Точка u називається першою точкою золотого перерізу, а точка v – другою.
Зауважимо,
що точка
 є, в свою чергу, другою точкою золотого
перерізу відрізка
є, в свою чергу, другою точкою золотого
перерізу відрізка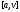 .
Дійсно, із означення золотого перерізу
i формул (7), (8) маємо нерівність
.
Дійсно, із означення золотого перерізу
i формул (7), (8) маємо нерівність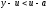 і рівність
і рівність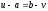 .
Тоді, враховуючи (9),
.
Тоді, враховуючи (9),
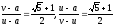 тобто
тобто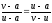
Аналогічно
можна показати, що точка
 є першою точкою золотого перерізу
відрізка
є першою точкою золотого перерізу
відрізка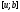 .
.
Знаючи
одну з точок золотого перерізу відрізка
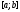 ,
іншу можна знайти за однією з формул:
,
іншу можна знайти за однією з формул:
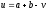 або
або
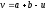 .
.
Використовуючи
розглянуті властивості золотого
перерізу, можна запропонувати такий
метод мінімізації унімодальної на
відрізку
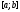 функції
функції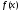 .
.
Нехай
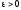 – задана точність відшукання точки
мінімуму. Покладемо на першому кроці
– задана точність відшукання точки
мінімуму. Покладемо на першому кроці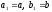 ,
знайдемо точки
,
знайдемо точки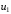 i
i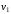 ,
наприклад, за формулами
,
наприклад, за формулами
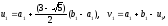 (10)
(10)
i
обчислимо значення функції
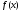 у цих точках:
у цих точках: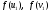 .
.
Якщо
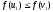 (рис. 8 а)), то покласти
(рис. 8 а)), то покласти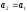 ,
,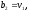
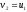 ,
,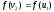 ,
знайти
,
знайти i обчислити
i обчислити .
.
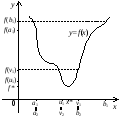
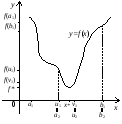
а) б)
Рис. 8.
Якщо
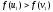 (рис 8 б)), то покласти
(рис 8 б)), то покласти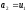 ,
,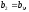
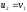 ,
,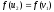 ,
знайти
,
знайти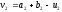 i обчислити
i обчислити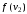 .
.
В
силу унімодальності функції
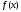 на
на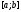 ,
відрізок
,
відрізок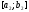 має хоча б одну спільну точку з множиною
має хоча б одну спільну точку з множиною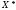 точок мінімуму
точок мінімуму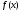 на
на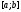 .
При цьому довжина відрізка
.
При цьому довжина відрізка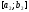 дорівнює
дорівнює
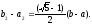 (11)
(11)
Дійсно,
при
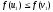
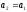 ,
,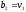 і тоді
і тоді
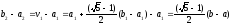 ,
,
а
при
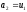 ,
,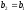 і тоді
і тоді
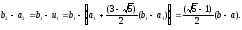
Нехай
вже визначений відрізок
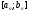 ,
знайдені точки
,
знайдені точки ,
значення
,
значення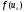 ,
,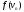 ,
при цьому, в загальному випадку,
,
при цьому, в загальному випадку,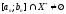 і
і
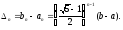 (12)
(12)
Якщо
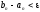 ,
то процес обчислень закінчується, i за
наближений розв'язок задачі можна взяти
точку
,
то процес обчислень закінчується, i за
наближений розв'язок задачі можна взяти
точку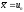 ,
якщо
,
якщо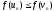 ,
або
,
або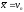 ,
якщо
,
якщо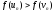 ,
при цьому похибка наближення
,
при цьому похибка наближення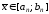 ,
з урахуванням (27.7), не перевищує величину
,
з урахуванням (27.7), не перевищує величину
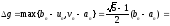
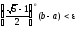 .
(13)
.
(13)
Якщо
ж
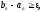 то при
то при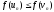 покласти
покласти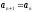 ,
,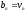 ,
,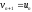 ,
,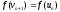 ,
знайти
,
знайти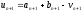 і обчислити
і обчислити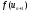 ,
інакше покласти
,
інакше покласти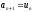 ,
,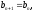
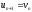 ,
,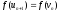 ,
знайти
,
знайти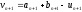 i обчислити
i обчислити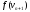 .
.
Після
чого треба повторити перевірку умови
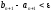 i т.д.
i т.д.
Як
видно з опису методу, на кожному його
кроці (крім першого) обчислюється лише
одне значення функції
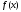 (на відміну від методу дихотомії).
Кількість кроків
(на відміну від методу дихотомії).
Кількість кроків методу золотого перерізу, яка забезпечує
задану точність знаходження наближення
до деякої точки
методу золотого перерізу, яка забезпечує
задану точність знаходження наближення
до деякої точки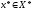 ,
задовольняє нерівність (див. (13))
,
задовольняє нерівність (див. (13))
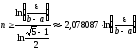 .
.
Розглянемо алгоритм, який реалізує описаний метод золотого перерізу.
Алгоритм 3
(методу золотого перерізу)
Нехай
задано
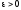 i відрізок
i відрізок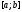 ,
на якому функція
,
на якому функція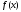 унімодальна.
унімодальна.
Крок
1. Знайти точки
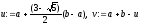 і обчислити
і обчислити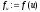 ,
,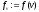 .
.
Крок
2. Якщо
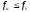 ,
то покласти
,
то покласти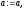
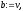
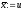 ,
,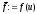 ,
,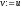 ,
,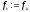 ,
знайти
,
знайти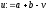 і обчислити
і обчислити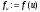 ;
;
інакше
(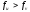 )
покласти
)
покласти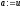 ,
,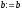 ,
, ,
,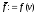 ,
,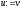 ,
,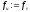 ,
знайти
,
знайти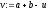 і обчислити
і обчислити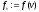 .
.
Крок
3. Якщо
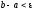 ,
то перейти на виконання кроку 4, інакше
перейти до виконання кроку 2.
,
то перейти на виконання кроку 4, інакше
перейти до виконання кроку 2.
Крок
4. Вивести
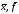 .
Кінець алгоритму.
.
Кінець алгоритму.
Зауваження.
На жаль чисельна реалізація описаного
алгоритму, а отже і методу золотого
перерізу, призводить до того, що він
стає практично незастосовним навіть
при невеликих
 .
Це викликано тим, що значення
.
Це викликано тим, що значення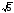 в ЕОМ обчислюється наближено і вже перші
точки ітераційного процесу (див.(27.6))
будуть знайдені з деякою похибкою, яка
при збільшенні
в ЕОМ обчислюється наближено і вже перші
точки ітераційного процесу (див.(27.6))
будуть знайдені з деякою похибкою, яка
при збільшенні досить швидко накопичується, а це
призводить до того, що порушується
властивість симетричності методу.
досить швидко накопичується, а це
призводить до того, що порушується
властивість симетричності методу.
Розглянемо
модифікований алгоритм методу золотого
перерізу, який у випадку порушення
симетричності методу, а, точніше, коли
на деякому кроці
 буде
буде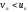 ,
перераховує для поточного відрізка
,
перераховує для поточного відрізка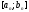 золотий переріз за формулами (27.6), що
забезпечує його практичну застосовність
до розв’язування задач одновимірної
мінімізації та перевагу перед методом
дихотомії за кількістю обчислень значень
функції
золотий переріз за формулами (27.6), що
забезпечує його практичну застосовність
до розв’язування задач одновимірної
мінімізації та перевагу перед методом
дихотомії за кількістю обчислень значень
функції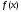 при заданій точності
при заданій точності .
.
Алгоритм 3
(модифікованого методу золотого перерізу)
Нехай
задано
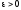 і відрізок
і відрізок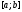 ,
на якому функція
,
на якому функція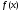 унімодальна.
унімодальна.
Крок
1. Знайти точки
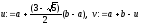 і обчислити
і обчислити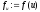 ,
,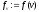 .
.
Крок
2. Якщо
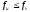 ,
то покласти
,
то покласти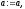
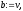
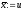 ,
,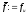 ,
,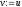 ,
,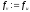 ,
знайти
,
знайти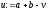 і якщо
і якщо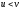 ,
то обчислити
,
то обчислити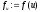 ;
;
інакше
(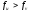 )
покласти
)
покласти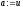 ,
,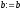 ,
,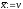 ,
,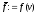 ,
,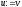 ,
,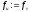 ,
знайти
,
знайти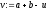 і якщо
і якщо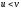 ,
то обчислити
,
то обчислити .
.
Крок
3. Якщо
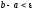 ,
то перейти на виконання кроку 5.
,
то перейти на виконання кроку 5.
Крок
4. Якщо
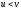 ,
то перейти до виконання кроку 2, інакше
перейти на виконання кроку 1.
,
то перейти до виконання кроку 2, інакше
перейти на виконання кроку 1.
Крок
5.Вивести
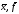 .
Кінець алгоритму.
.
Кінець алгоритму.
Зауваження. Розглянутий алгоритм методу золотого перерізу можна застосовувати на практиці і для більш широкого класу неперервних функцій, але отриманий при цьому розв'язок може виявитися далеким від точку глобального мінімуму.
Метод Фібоначчі.
У тих випадках, коли обчислення значень функції пов'язане з певними труднощами, важливого значення набувають найбільш економічні методи, які дозволяють розв'язати задачу мінімізації з потрібною точністю при якомога меншій кількості обчислень значень функції, що мінімізується. Розглянемо один з таких методів, який є оптимальним, для класу унімодальних функцій i тісно пов'язаний із числами Фібоначчі.
Як відомо, числа Фібоначчі визначаються співвідношеннями:
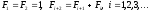 (14)
(14)
Наведемо кілька перших чисел Фібоначчі:
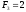 ,
,
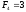 ,
,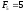 ,
,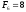 ,
,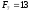 ,
,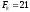 ,
,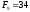 ,
,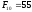 ,
, ,
,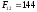 ,
,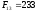 ,
,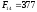 ,
,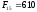 ,…,
,…,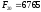 ,…,
,…,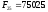
За
методом індукції можна довести, що
 -
те число Фібоначчі можна подати у вигляді
:
-
те число Фібоначчі можна подати у вигляді
:
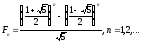 –формула Біне.
–формула Біне.
Звідси
випливає, що при досить великому

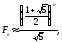 (15)
(15)
тобто
числа Фібоначчі із зростанням
 зростають досить швидко.
зростають досить швидко.
Нехай
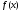 – унімодальна на відрізку
– унімодальна на відрізку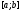 функція i задано число
функція i задано число обчислень значень цієї функції, яке
повинно забезпечити необхідну точність
відшукання наближення деякої точки
мінімуму
обчислень значень цієї функції, яке
повинно забезпечити необхідну точність
відшукання наближення деякої точки
мінімуму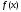 на
на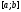 .
.
Метод
Фібоначчі, як i метод золотого перерізу,
відноситься до класу симетричних
методів i визначається
заданням на відрізку
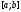 двох точок, симетричних відносно його
середини (рис. 9):
двох точок, симетричних відносно його
середини (рис. 9):
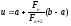 і
і
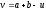
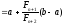 .
.

Рис. 9.
Далі на кожному кроці методу точка чергового обчислення вибирається симетрично відносно середини поточного відрізка локалізації до точки, яка лежить внутрі цього відрізка і знайдена на попередньому кроці.
Розглянемо
перші кроки методу Фібоначчі. Нехай
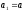 ,
,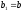 .
Знайдемо
.
Знайдемо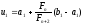 ,
,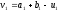 ,
де
,
де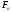 ,
,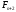 –
відповідні числа Фібоначчі при заданому
–
відповідні числа Фібоначчі при заданому ,
які знаходяться за допомогою рекурентного
співвідношення (14) або за формулою Біне.
,
які знаходяться за допомогою рекурентного
співвідношення (14) або за формулою Біне.
Якщо
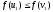 ,
то наступним відрізком локалізації є
відрізок
,
то наступним відрізком локалізації є
відрізок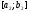 ,
де
,
де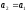 ,
,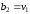 .
У цьому випадку точка
.
У цьому випадку точка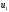 буде визначати точку
буде визначати точку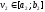 ,
тобто
,
тобто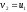 ,
а точка
,
а точка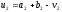 .
Крім того, можна легко перевірити, що
.
Крім того, можна легко перевірити, що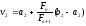 .
.
Якщо
ж
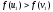 ,
то наступним відрізком локалізації є
відрізок
,
то наступним відрізком локалізації є
відрізок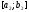 ,
де
,
де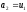 ,
,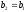 .
У цьому випадку точка
.
У цьому випадку точка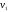 буде визначати точку
буде визначати точку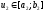 ,
тобто
,
тобто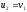 ,
а точка
,
а точка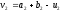 .
Крім того, можна легко перевірити, що
.
Крім того, можна легко перевірити, що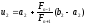 .
.
За
методом індукції можна показати, що на
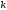 -му
кроці методу Фібоначчі буде отримана
трійка
-му
кроці методу Фібоначчі буде отримана
трійка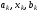 ,
яка локалізує хоча б одну точку
,
яка локалізує хоча б одну точку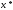 з множини
з множини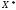 точок мінімуму функції
точок мінімуму функції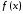 i така, що
i така, що
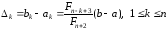 , (16)
, (16)
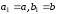 ,
а точка
,
а точка
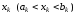 ,
для якої
,
для якої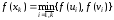 ,
,
співпадає з однією з точок
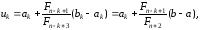 (17)
(17)
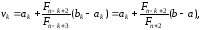
які розташовані на відрізку
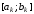 симетрично відносно його середини. При
симетрично відносно його середини. При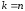 процес закінчується. В цьому випадку
згідно формул (14), (16), (17) довжина відрізка
процес закінчується. В цьому випадку
згідно формул (14), (16), (17) довжина відрізка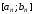 дорівнює
дорівнює
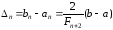 , (18)
, (18)
а точки

співпадають
(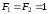 )
і є серединою відрізка
)
і є серединою відрізка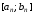 .
.
За
наближений розв'язок задачі пошуку
мінімуму функції
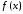 на проміжку
на проміжку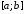 приймають величину
приймають величину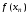 ,
де
,
де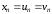 .
При цьому похибка наближення
.
При цьому похибка наближення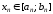 ,
з урахуванням (18), не перевищує величину
,
з урахуванням (18), не перевищує величину
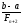 .
.
Зауваження.
Після
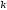 кроків
методу Фібоначчі відношення довжини
відрізка локалізації
кроків
методу Фібоначчі відношення довжини
відрізка локалізації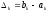 (див. (28.3)) до довжини більшого відрізка
(див. (28.3)) до довжини більшого відрізка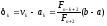 (див. (17)), дорівнює
(див. (17)), дорівнює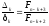 .
Тоді, враховуючи (15), при досить великих
.
Тоді, враховуючи (15), при досить великих маємо
маємо
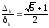 .
.
Крім
того,
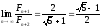 ,
,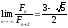 ,
тобто при досить великому
,
тобто при досить великому початкові точки
початкові точки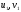 методів Фібоначчі та золотого перерізу
практично співпадають.
методів Фібоначчі та золотого перерізу
практично співпадають.
Це зауваження свідчить про тісний зв’язок між методами Фібоначчі та золотого перерізу.
Розглянемо алгоритм, який реалізує метод Фібоначчі.
Алгоритм 5
(методу Фібоначчі)
Нехай
задано
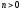 – число обчислень значень функції
– число обчислень значень функції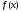 i відрізок
i відрізок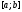 ,
на якому ця функція унімодальна.
,
на якому ця функція унімодальна.
Крок
0. Покласти
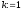 .
.
Крок 1. Знайти точки
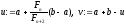
і
обчислити
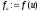 ,
,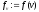 .
.
Крок
2. Якщо
 ,
то покласти
,
то покласти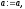
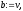
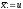 ,
,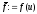 ,
,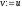 ,
, ,
знайти
,
знайти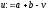 і обчислити
і обчислити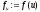 ;
;
інакше
покласти
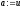 ,
,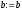 ,
,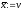 ,
,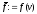 ,
,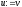 ,
,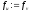 ,
знайти
,
знайти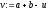 і обчислити
і обчислити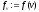 .
.
Крок
3. Якщо
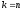 ,
то перейти на виконання кроку 4, інакше
покласти
,
то перейти на виконання кроку 4, інакше
покласти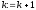 перейти до виконання кроку 2.
перейти до виконання кроку 2.
Крок
4.Вивести
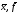 .
Кінець алгоритму.
.
Кінець алгоритму.
Зауваження.
1. Числа
Фібоначчі
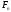 ,
, при заданому
при заданому на кроці 1 алгоритму 5 знаходяться за
допомогою рекурентного співвідношення
(14) або за формулою Біне.
на кроці 1 алгоритму 5 знаходяться за
допомогою рекурентного співвідношення
(14) або за формулою Біне.
2.
При практичній реалізації описаного
алгоритму, а отже і методу Фібоначчі,
треба мати на увазі, що число
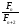 ,
взагалі кажучи, є нескінченним періодичним
дробом, тому перша точка
,
взагалі кажучи, є нескінченним періодичним
дробом, тому перша точка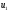 буде знайдена наближено. В зв’язку з
цим похибка у визначенні цієї точки, як
правило, призводить до швидкого зростання
похибки на наступних ітераціях методу,
і вже при не дуже великих
буде знайдена наближено. В зв’язку з
цим похибка у визначенні цієї точки, як
правило, призводить до швидкого зростання
похибки на наступних ітераціях методу,
і вже при не дуже великих симетричність методу порушується.
симетричність методу порушується.
Розглянемо
модифікований алгоритм 5, який у
випадку порушення симетричності методу,
а, точніше, коли на деякому кроці
 буде
буде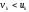 ,
обчислює для поточного відрізка
,
обчислює для поточного відрізка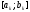 точку
точку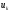 за рекурентним співвідношенням (17), а
точку
за рекурентним співвідношенням (17), а
точку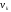 за формулою
за формулою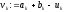 ,
що забезпечує його практичну застосовність
до розв’язування задач одновимірної
мінімізації.
,
що забезпечує його практичну застосовність
до розв’язування задач одновимірної
мінімізації.
Алгоритм 6
(модифікованого методу Фібоначчі)
Нехай
задано
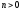 – число обчислень значень унімодальної
функції
– число обчислень значень унімодальної
функції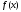 i відрізок
i відрізок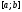 .
.
Крок
0. Покласти
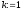 .
.
Крок 1. Знайти точки
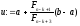 ,
,
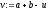
і
обчислити
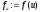 ,
,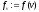 .
.
Крок
2. Якщо
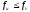 ,
то покласти
,
то покласти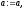
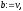
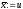 ,
,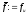 ,
,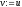 ,
,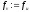 ,
знайти
,
знайти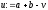 і якщо
і якщо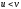 ,
то обчислити
,
то обчислити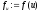 ;
;
інакше
(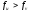 )
покласти
)
покласти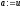 ,
,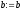 ,
,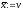 ,
,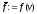 ,
,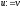 ,
,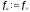 ,
знайти
,
знайти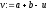 і якщо
і якщо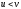 ,
то обчислити
,
то обчислити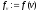 .
.
Крок
3. Якщо
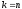 ,
то перейти на виконання кроку 5.
,
то перейти на виконання кроку 5.
Крок
4. Покласти
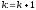 .
Якщо
.
Якщо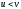 ,
то перейти до виконання кроку 2, інакше
перейти на виконання кроку 1.
,
то перейти до виконання кроку 2, інакше
перейти на виконання кроку 1.
Крок
5. Вивести
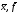 .
Кінець алгоритму.
.
Кінець алгоритму.
Зауваження.
1.
Якщо задана точність обчислень результату
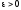 ,
то з (18) випливає, що число
,
то з (18) випливає, що число в методі Фібоначчі треба вибирати з
умови
в методі Фібоначчі треба вибирати з
умови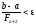 .
.
2. Алгоритм 6 можна застосовувати на практиці і для більш широкого класу неперервних функцій, але отриманий при цьому розв'язок може виявитися далеким від точку глобального мінімуму.
Метод парабол.
Існують
досить широкі класи функцій, які зручно
апроксимувати, наприклад, многочленом
другого степеня. Тоді за наближене
значення мінімуму функції
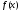 доцільно взяти точку мінімуму цього
многочлена. Оскільки графік многочлена
другого степеня має вигляд параболи,
то такий метод називаютьметодом
парабол. Цей метод дає
хороші результати при мінімізації
гладких унімодальних функцій, тому що
в околі точки
доцільно взяти точку мінімуму цього
многочлена. Оскільки графік многочлена
другого степеня має вигляд параболи,
то такий метод називаютьметодом
парабол. Цей метод дає
хороші результати при мінімізації
гладких унімодальних функцій, тому що
в околі точки
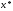 графіки таких функцій досить "близькі"
до параболи.
графіки таких функцій досить "близькі"
до параболи.
Для
побудови апроксимуючого многочлена
другого степеня необхідно мати три
точки
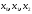 такі, що
такі, що
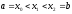 ,
,
i
значення функції
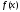 в цих точках
в цих точках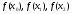 .
.
Тоді інтерполяційний многочлен Лагранжа другого степеня має вигляд:
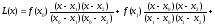
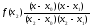 ,
,
або у більш зручній для диференціювання формі:
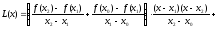
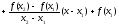 . (19)
. (19)
Нехай
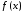 унімодальна на
унімодальна на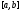 функція i
функція i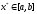 .
.
Означення 2.
Трійка чисел
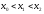 називаєтьсявдалою,
якщо
називаєтьсявдалою,
якщо
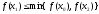
і
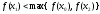 .
.
Остання
умова означає, що точки
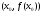 ,
,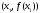 ,
,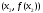 не лежать на прямій, паралельній осі
абсцис (рис. 10).
не лежать на прямій, паралельній осі
абсцис (рис. 10).
Із
означення вдалої трійки випливає, що
точка
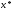 мінімуму функції
мінімуму функції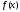 міститься всередині відрізка
міститься всередині відрізка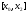 .
.
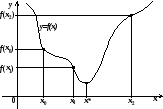
Рис. 10.
Нехай
знайдена вдала трійка чисел
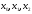 .
Тоді хоча б одна з нерівностей
.
Тоді хоча б одна з нерівностей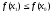 і
і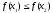 строга i коефіцієнт при старшому члені
многочлена (19) додатній.
строга i коефіцієнт при старшому члені
многочлена (19) додатній.
Визначивши
похідну многочлена (19) i прирівнявши її
до нуля, можна показати, що мінімум
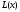 досягається в точці
досягається в точці
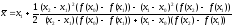 , (20)
, (20)
при
цьому
 .
.
Отримана
точка i обирається за точку наступного
обчислення значення функції
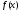 (рис. 11).
(рис. 11).
Можливий
випадок, коли
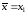 (рис. 12). Тоді за точку наступного
обчислення обирається одна з точок
(рис. 12). Тоді за точку наступного
обчислення обирається одна з точок
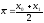 або
або
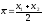 .
.
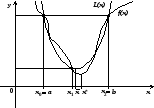
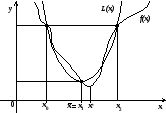
Рис. 11. Рис. 12.
Далі
із точок
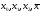 треба вибрати нову вдалу трійку
треба вибрати нову вдалу трійку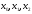 i повторити обчислення за формулою (20)
і т.д.
i повторити обчислення за формулою (20)
і т.д.
Закінчити
пошук наближеного значення точки
мінімуму
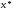 можна, якщо виконується умова
можна, якщо виконується умова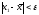 i покласти при цьому
i покласти при цьому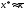 ,
,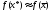 .
.
Метод
парабол доцільно застосовувати після
того, як знайдено відрізок локалізації
мінімуму досить малої довжини. Наприклад,
такий відрізок може бути отриманий
після
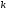 кроків методу дихотомії або золотого
перерізу.
кроків методу дихотомії або золотого
перерізу.
Чисельні
експерименти показують, що якщо функція
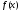 добре апроксимується параболою в околі
множини розв’язків
добре апроксимується параболою в околі
множини розв’язків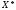 ,
то цей метод виявляється більш ефективним,
ніж інші методи мінімізації.
,
то цей метод виявляється більш ефективним,
ніж інші методи мінімізації.
Розглянемо один з алгоритмів, який реалізує метод парабол.
Спочатку
опишемо процедуру знаходження вдалої
трійки для функції
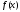 на відрізку
на відрізку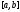 локалізації точки мінімуму цієї функції.
локалізації точки мінімуму цієї функції.
Нехай
задані точки
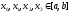 такі, що
такі, що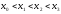 ,
і відомі значення функції
,
і відомі значення функції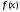 у цих точках:
у цих точках: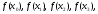 причому
причому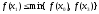 i
i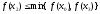 .
.
Якщо
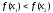 ,
то покласти
,
то покласти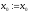 ,
,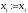 ,
,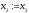 .
Якщо
.
Якщо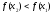 ,
то покласти
,
то покласти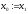 ,
,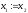 ,
,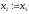 .
Якщо
.
Якщо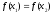 ,
то
,
то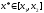 i будь-яка трійка
i будь-яка трійка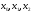 або
або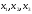 буде вдалою. При цьому вибирають ту,
якій відповідає менший з відрізків
буде вдалою. При цьому вибирають ту,
якій відповідає менший з відрізків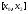 або
або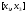 .
.
Алгоритм 6.
(методу парабол)
Нехай
задані відрізок
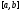 локалізації точки мінімуму функції
локалізації точки мінімуму функції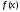 і
і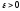 (досить мале число).
(досить мале число).
Крок 0.
На відрізку
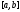 визначити першу вдалу трійку
визначити першу вдалу трійку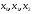 і обчислити
і обчислити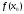 ,
,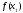 ,
,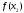 .
.
Крок 1. Знайти точку
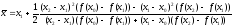
і
обчислити
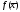 .
.
Крок 2.
Якщо
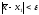 ,
то покласти
,
то покласти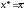 ,
,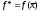 i кінець алгоритму, інакше якщо
i кінець алгоритму, інакше якщо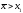 ,
то покласти
,
то покласти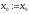 ,
,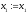 ,
,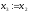 ,
,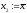 ,
інакше покласти
,
інакше покласти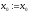 ,
,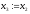 ,
,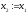 ,
,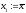 .
.
Крок 3.
Для одержаних точок
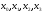 знайти вдалу трійку
знайти вдалу трійку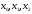 ,
обчислити значення
,
обчислити значення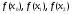 і перейти до виконання кроку 1.
і перейти до виконання кроку 1.
Кінець алгоритму.
