1. Унімодальні функції та їх властивості

Нехай функція визначена і скінченна на множині.

Означення 1. Функція називаєтьсяунімодальною на відрізку , якщо вона неперервна на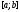і якщо існують точкиітакі, що

1) якщо , то на відрізкустрого монотонно спадає;

2) якщо , то на відрізкустрого монотонно зростає;

3) якщ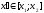о , то.

На рис. 1 наведено приклади унімодальних функцій, а на рис. 2 – ні. Згідно означення 1 відрізки ,є відрізками монотонності, а відрізокє відрізком сталості функції. Як видно з рис. 1, для унімодальних функцій можливі випадки, коли один або два з відрізківвироджуються в точку.

З означення 1 випливає, що для унімодальних функцій точки локального мінімуму є точками глобального мінімуму, при цьому множина точок мінімуму 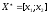(рис. 1). Очевидно, що опуклі на проміжкуфункції є унімодальними на цьому проміжку.

Якщо в означенні 1 , то функціяназивається строго унімодальною на відрізку (рис. 1 а), г)).

З означення строго унімодальної функції випливає, що така функція не містить ділянок сталості і в неї єдина точка локального мінімуму. Очевидно, що строго і сильно опуклі функції є строго унімодальними.

Для класу унімодальних функцій мають місце наступні твердження.

Лема 1. Якщо функція унімодальна на відрізку, то вона унімодальна і на відрізку .

Лема 2. Нехай функція унімодальна на відрізкуі. Тоді

1) якщото, а якщото;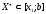

2) якщо то, тобто відрізокмістить хоча б одну точку.

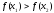Наслідок. Якщо то існує точкатака, що, а якщото.

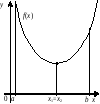
a) б)

в) г)

Рис. 1.

а) б)

Рис. 2.

На практиці для перевірки унімодальності диференційованих на відрізку функцій використовують наступні твердження.

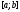Лема 3. Якщо функція диференційована наі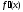не спадає при всіх, то– унімодальна.

Лема 4. Якщо – двічі диференційована функція на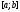іпри всіх, то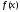– унімодальна.

Приклад 1. Довести, що функція

унімодальна на відрізку .

Оскільки функція двічі диференційована, то знайдемо спочатку першу похідну

,

а потім другу

.

Оскільки 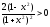ідля всіх, то– унімодальна на цьому відрізку згідно леми 4.

Зауваження. Леми 3 і 4 є достатніми умовами опуклості диференційованих і двічі диференційованих функцій відповідно (див. наслідки теорем 1 і 6)

Методи мінімізації унімодальних функцій та аналіз їх ефективності відіграють значну роль, оскільки такі функції часто зустрічаються при розв'язуванні практичних задач. Крім того, припущення про унімодальність функції в околі точки мінімуму є, взагалі кажучи, досить природним (див. рис. 25.2). Тому відшукання такого околу, який називається відрізком локалізації точки мінімуму, є важливим попереднім етапом розв’язування задачі одновимірної мінімізації.

Пошук відрізка локалізації точки мінімуму. Оскільки на практиці множина в задачі одновимірної мінімізації

, (1)

де – унімодальна функція, як правило, необмежена, то важливим етапом її розв'язування є визначеннявідрізка локалізації точки мінімуму, тобто відрізка, який містить хоча б одну точку , де– множина розв’язків задачі (1).

Враховуючи лему 2, можна побудувати скінченний процес, що дозволяє знайти відрізок 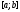локалізації точки мінімуму. Розглянемо один з варіантів такого процесу для випадку, коли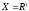і в довільній точціне відомий напрям спадання функції. Процес починається з точки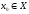і спочатку визначається напрям спадання функції(якщо він існує), а потім продовжується доти, поки не буде пройдена точка мінімуму цільової функції. Ознакою цього є те, що значення функції в новій точці буде більше ніж у попередній. Якщо в процесі роботи буде одержано дві сусідні точки, в яких значення функції рівні, то в якості відрізка локалізації визначається відрізок з кінцями в цих точках. Згідно означення 1 такий відрізок містить принаймні одну точку. Це дає змогу уникнути зациклювання процесу, якщо множинамає необмеженій проміжок сталості цільової функції. 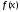Результатом процесу будуть точки,– кінці відрізка, який містить хоча б одну точку, і значення функціїв цих точках:і.

Алгоритм 1

(пошуку відрізка локалізації точки мінімуму)

Нехай задані довільне початкове наближення 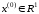,і величина кроку.

Крок 0. Покласти і обчислити.

Крок 1. Якщо то покласти,і перейти до виконання кроку 5.

Крок 2. Покласти 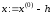і обчислити.

Крок 3. Якщо то покласти,,і перейти до виконання кроку 5.

Крок 4. Покласти і перейти до виконання кроку 0.

Крок 5. Покласти і обчислити .

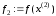Крок 6. Якщо , то покласти,,,і перейти до виконання кроку 5.

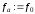Крок7. Якщо , то покласти,,, інакше покласти,,,.

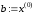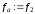Кінець алгоритму.

Зауваження:

1. Трійка чисел , яка одержується в результаті роботи алгоритму, євдалою трійкою і використовується в деяких методах одновимірної мінімізації, зокрема в методі парабол.

2. Якщо початкове наближення знаходиться в- околі точки мінімумуфункції(де- досить мале додатне число), то алгоритм 2 можна застосовувати безпосередньо для знаходження наближеного значенняз точністю до. Для цього до алгоритму 2 треба ввести ще один параметр- точність наближеного розв'язку і після кроку 7 добавити ще один крок:

Крок 8.Якщо , то покласти,і кінець алгоритму, інакше вивести.

3. Алгоритм 1 погано працює у випадку коли 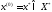(операціяі повернення на крок 0 продовжується доти, поки ЕОМ буде розрізняти значенняi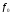). Щоб запобігти цьому, крок 4 алгоритму 2 можна замінити на такий:

Крок 4. Якщо 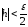, то покласти,і кінець алгоритму, інакше покластиі перейти на крок 0.