
І. Теоретичні відомості.
1. Економічна і геометрична інтерпретації задач теорії ігор.
Якщо є кілька конфліктуючих сторін (осіб), кожна з який приймає деяке рішення, обумовлене заданим набором правил, і кожній з сторін відомий можливий кінцевий стан конфліктної ситуації з заздалегідь визначеними для кожної із сторін платежами, то говорять, що має місце гра. Задача теорії ігор полягає у виборі такої лінії поведінки даного гравця, відхилення від якої може лише зменшити його виграш.
Означення 1. Ситуація називається конфліктною, якщо в ній беруть участь сторони, інтереси яких цілком чи частково протилежні.
Означення 2. Гра — це дійсний чи формальний конфлікт, у якому є принаймні два учасники (гравця), кожний з який прагне до досягнення власних цілей.
Означення 3. Припустимі дії кожного з гравців, спрямовані на досягнення деякої мети, називаються правилами гри.
Означення 4. Кількісна оцінка результатів гри називається платежем.
Означення 5. Гра називається парною, якщо в ній беруть участь тільки дві сторони (дві особи).
Означення 6. Парна гра називається грою з нульовою сумою, якщо сума платежів дорівнює нулю, тобто якщо програш одного гравця дорівнює виграшу другого.
Ми будемо розглядати саме парні ігри з нульовою сумою.
Означення 7. Однозначний опис вибору гравця в кожній з можливих ситуацій, при якій він повинен зробити особистий хід, називається стратегією гравця.
Означення 8. Стратегія гравця називається оптимальною, якщо при багаторазовому повторенні гри вона забезпечує гравцю максимально можливий середній виграш (чи, що те ж саме, мінімально можливий середній програш).
Нехай є
два гравці, один з яких може вибрати
i-ту
стратегію із m
своїх можливих стратегій (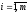 ),
а другий,
не знаючи вибору першого,
вибирає j-ту
стратегію із n
своїх
можливих стратегій (
),
а другий,
не знаючи вибору першого,
вибирає j-ту
стратегію із n
своїх
можливих стратегій (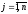 ).
У результаті
перший гравець виграє величину
).
У результаті
перший гравець виграє величину
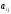 ,адругий
програє цю ж
величину.
,адругий
програє цю ж
величину.
З чисел
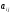 складемо
матрицю
складемо
матрицю

Рядки матриці А відповідають стратегіям першого гравця, а стовпці — стратегіям другого. Ці стратегії називаються чистими.
Означення 9. Матриця А називається платіжною (чи матрицею гри).
Означення 10.
Гру, обумовлену
матрицею А,
що має m
рядків і n
стовпчиків,
називають кінцевою грою розмірності
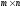 .
.
Означення 11.
Число
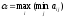 називаєтьсянижньою
ціною гри
або максиміном,
а відповідна йому стратегія (рядок) —
максимінною.
називаєтьсянижньою
ціною гри
або максиміном,
а відповідна йому стратегія (рядок) —
максимінною.
Означення 12.
Число
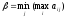 називається верхньою
ціною гри
або мінімаксом,
а відповідна
йому стратегія гравця (стовпчик) —
мінімаксною.
називається верхньою
ціною гри
або мінімаксом,
а відповідна
йому стратегія гравця (стовпчик) —
мінімаксною.
Теорема 1. Нижня ціна гри завжди не перевершує верхньої ціни гри.
Означення 13
Якщо
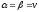 ,
то числоv
називається ціною
гри.
,
то числоv
називається ціною
гри.
Означення 14.
Гра, для якої
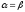 ,
називається грою ізсідловою
точкою.
,
називається грою ізсідловою
точкою.
Для гри із сідловою точкою знаходження розв’язку полягає у виборі максимінної і мінімаксної стратегій, що є оптимальними.
Якщо гра, задана матрицею, не має сідлової точки, то для знаходження її розв’язку використовуються мішані стратегії.
Означення 15. Вектор, кожна з компонентів якого показує відносну частоту використання гравцем відповідної чистої стратегії, називається змішаною стратегією даного гравця.
З даного визначення
безпосередньо випливає,
що сума компонентів зазначеного
вектора дорівнює одиниці, а самі
компоненти не від’ємні. Звичайно змішану
стратегію першого гравця позначають
як вектор
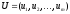 ,
а другого
гравця — як вектор
,
а другого
гравця — як вектор
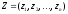 ,
де
,
де
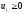 (
(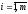 ),
),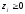 (
(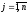 ),
),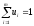 ,
,
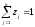
Якщо
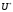 — оптимальна стратегія першого гравця,
а
— оптимальна стратегія першого гравця,
а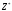 — оптимальна стратегія другого гравця,
то число
— оптимальна стратегія другого гравця,
то число
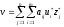
є ціною гри.
Визначення оптимальних стратегій і ціни гри якраз і складає процес знаходження розвозку гри.
Теорема 2. Всяка матрична гра з нульовою сумою має розв’язок в мішаних стратегіях.
Теорема 3.
Для того
щоб число v
було ціною гри, а
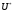 і
і
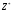 —
оптимальними стратегіями, необхідно і
достатньо виконання нерівностей
—
оптимальними стратегіями, необхідно і
достатньо виконання нерівностей
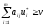 (
(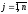 )
і
)
і
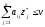 (
(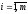 )
)
Якщо теорема 2
дає відповідь на питання про існування
розв’язку
гри, то наступна теорема дає відповідь
на питання, як знайти цей розв’язок
для ігор
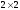 ,
,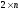 і
і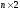 .
.
Теорема 4. Якщо один із гравців застосовує оптимальну мішану стратегію, то його виграш дорівнює ціні гри v не залежно від того, з якими частотами буде застосовувати другий гравець стратегії, що ввійшли в оптимальну (у тому числі і чисті стратегії).
І. Теоретичні відомості
Загальна характеристика задач динамічного програмування.
У задачах лінійного програмування, ми знаходили розв’язок як би в один етап або за один крок. Такі задачі отримали назву одноетапні або однокрокові.
На відміну від цих задач задачі динамічного програмування є багатоетапними або багатокроковими. Іншими словами, знаходження розв’язку конкретних задач методами динамічного програмування включає декілька етапів або кроків, на кожному з яких визначається розв’язок деякої частинної задачі, обумовленої початковою. Тому термін «динамічне програмування» не стільки визначає особливий тип задач, скільки характеризує методи знаходження розв’язку окремих класів задач математичного програмування, які можуть відноситися до задач як лінійного, так і нелінійного програмування. Не дивлячись на це, доцільно дати спільну постановку задачі динамічного програмування і визначити єдиний підхід до її розв’язання.
Нехай
задана фізична система
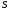 знаходиться в деякому початковому стані
знаходиться в деякому початковому стані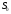 і є керованою. Таким чином, завдяки
здійсненню деякого управління
і є керованою. Таким чином, завдяки
здійсненню деякого управління вказана система переходить з початкового
стану
вказана система переходить з початкового
стану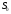 в кінцевий стан
в кінцевий стан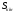 .
При цьому якість кожного з управлінь,
що реалізовуються, характеризується
відповідним значенням функції
.
При цьому якість кожного з управлінь,
що реалізовуються, характеризується
відповідним значенням функції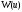 .
Задача полягає в тому, щоб з множини
можливих управлінь
.
Задача полягає в тому, щоб з множини
можливих управлінь знайти таке
знайти таке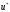 ,
при якому функція
,
при якому функція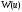 набуває екстремального (максимального
або мінімального) значення
набуває екстремального (максимального
або мінімального) значення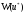 .
Сформульована задача і є загальною
задачею динамічного програмування.
.
Сформульована задача і є загальною
задачею динамічного програмування.
Знаходження розв’язку задач методом динамічного програмування.
Розглянемо тепер в загальному вигляді розв’язок цієї задачі динамічного програмування. Для цього введемо деякі позначення і зробимо необхідні для подальшого викладення припущення.
Вважатимемо,
що перебування даної системи
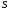 на
на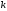 -му
кроці (
-му
кроці (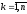 )
визначається сукупністю чисел
)
визначається сукупністю чисел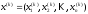 ,
які отримані в результаті реалізації
управління
,
які отримані в результаті реалізації
управління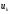 ,
що забезпечило перехід системи
,
що забезпечило перехід системи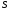 із стану
із стану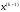 в стан
в стан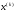 .
При цьому передбачатимемо, що стан
.
При цьому передбачатимемо, що стан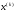 ,
в який перейшла система
,
в який перейшла система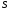 ,
залежить від даного стану
,
залежить від даного стану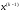 і вибраного управління
і вибраного управління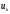 і не залежить від того, яким чином система
і не залежить від того, яким чином система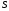 прийшла в стан
прийшла в стан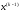 .
.
Далі,
вважатимемо, що якщо в результаті
реалізації
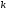 -го
кроку забезпечений певний дохід або
виграш, також залежний від початкового
стану системи
-го
кроку забезпечений певний дохід або
виграш, також залежний від початкового
стану системи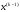 і вибраного управління
і вибраного управління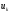 і рівний
і рівний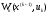 ,
то спільний дохід або виграш за
,
то спільний дохід або виграш за кроків складає
кроків складає
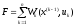 . (1)
. (1)
Таким чином, ми сформулювали дві умови, якими повинна задовольняти дана задача динамічного програмування. Першу умову зазвичай називають умовою відсутності наслідків, а другу – умовою адитивності цільової функції задачі.
Виконання
для задачі динамічного програмування
першої умови дозволяє сформулювати для
неї принцип оптимальності Беллмана.
Перш ніж зробити це, дамо визначення
оптимальної стратегії управління. Під
такою стратегією розумітимемо сукупність
управлінь
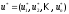 ,
в результаті реалізації яких система
,
в результаті реалізації яких система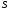 за
за кроків переходить з початкового стану
кроків переходить з початкового стану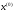 в кінцевий
в кінцевий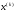 і при цьому функція (1) набуває найбільшого
значення.
і при цьому функція (1) набуває найбільшого
значення.
Принцип оптимальності. Яким би не був стан системи перед черговим кроком, треба вибрати управління на цьому кроці так, щоб виграш на даному кроці плюс оптимальний виграш на всіх подальших кроках був максимальним.
Звідси
витікає, що оптимальну стратегію
управління можна отримати, якщо спочатку
знайти оптимальну стратегію управління
на
 -му
кроці, потім на двох останніх кроках,
потім на трьох останніх кроках і так
далі, аж до першого кроку. Таким чином,
розв’язок даної задачі динамічного
програмування доцільно починати з
визначення оптимального розв’язок на
останньому,
-му
кроці, потім на двох останніх кроках,
потім на трьох останніх кроках і так
далі, аж до першого кроку. Таким чином,
розв’язок даної задачі динамічного
програмування доцільно починати з
визначення оптимального розв’язок на
останньому, -му
кроці. Для того, щоб знайти цей розв’язок,
очевидно, потрібно зробити різні
припущення про те, як міг закінчитися
передостанній крок, і з урахуванням
цього вибрати управління
-му
кроці. Для того, щоб знайти цей розв’язок,
очевидно, потрібно зробити різні
припущення про те, як міг закінчитися
передостанній крок, і з урахуванням
цього вибрати управління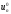 ,
що забезпечує максимальне значення
функції
,
що забезпечує максимальне значення
функції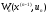 .
Таке управління
.
Таке управління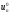 ,
вибране при певних припущеннях про те,
як закінчився попередній крок, називається
умовно оптимальним управлінням. Отже,
принцип оптимальності вимагає знаходити
на кожному кроці умовне оптимальне
управління для будь-якого з можливих
результатів попереднього кроку.
,
вибране при певних припущеннях про те,
як закінчився попередній крок, називається
умовно оптимальним управлінням. Отже,
принцип оптимальності вимагає знаходити
на кожному кроці умовне оптимальне
управління для будь-якого з можливих
результатів попереднього кроку.
Щоб
це можна було здійснити практично,
необхідно дати математичне формулювання
принципу оптимальності. Для цього
введемо деякі додаткові позначення.
Позначимо через
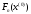 максимальний дохід, що отримується за
максимальний дохід, що отримується за кроків під час переходу системи
кроків під час переходу системи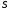 з початкового стану
з початкового стану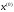 в кінцевий стан
в кінцевий стан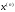 при реалізації оптимальної стратегії
управління
при реалізації оптимальної стратегії
управління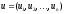 ,
а через
,
а через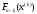 – максимальний дохід, що отримується
при переході з будь-якого стану
– максимальний дохід, що отримується
при переході з будь-якого стану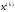 в кінцевий стан
в кінцевий стан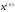 при оптимальній стратегії управління
на
при оптимальній стратегії управління
на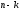 кроках, що залишилися. Тоді
кроках, що залишилися. Тоді
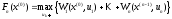 . (2)
. (2)
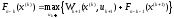 ,
(
,
(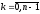 ). (3)
). (3)
Останній вираз є математичним записом принципу оптимальності і носить назву основного функціонального рівняння Беллмана або рекурентного співвідношення. Використовуючи дане рівняння, знаходимо розв’язок даної задачі динамічного програмування. Зупинимося на цьому детальніше.
Вважаючи
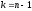 в рекурентному співвідношенні (3),
отримуємо наступне функціональне
рівняння:
в рекурентному співвідношенні (3),
отримуємо наступне функціональне
рівняння:
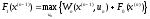 ,. (4)
,. (4)
У
цьому рівнянні
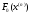 будемо вважати відомим. Використовуючи
тепер рівняння (4) і розглядаючи всі
допустимі стани системи
будемо вважати відомим. Використовуючи
тепер рівняння (4) і розглядаючи всі
допустимі стани системи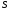 на
на -му
кроці
-му
кроці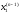 ,
,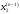 ,
…
,
…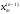 ,
…, знаходимо умовні оптимальні розв’язки
,
…, знаходимо умовні оптимальні розв’язки
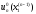 ,
,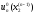 ,
…,
,
…,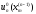 ,
…
,
…
і відповідні значення функції (4)
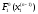 ,
,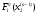 ,
…,
,
…,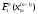 ,
…
,
…
Таким
чином, на
 -му
кроці знаходимо умовно оптимальне
управління при будь-якому допустимому
стані системи
-му
кроці знаходимо умовно оптимальне
управління при будь-якому допустимому
стані системи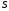 після
після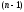 -го
кроку. Іншими словами, в якому б стані
система не опинилася після
-го
кроку. Іншими словами, в якому б стані
система не опинилася після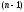 -го
кроку, нам вже відомо, яке слід прийняти
рішення на
-го
кроку, нам вже відомо, яке слід прийняти
рішення на -му
кроці. Відомо також і відповідне значення
функції (4).
-му
кроці. Відомо також і відповідне значення
функції (4).
Переходимо
тепер до розгляду функціонального
рівняння при
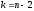 :
:
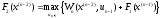 ,. (5)
,. (5)
Для
того, щоб знайти значення
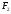 для всіх допустимих
значень
для всіх допустимих
значень
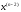 ,
очевидно, необхідно знати
,
очевидно, необхідно знати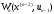 і
і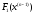 .
Що стосується значень
.
Що стосується значень
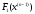 то
ми їх вже визначили. Тому потрібно
провести обчислення
то
ми їх вже визначили. Тому потрібно
провести обчислення при деякому наборі допустимих значень
при деякому наборі допустимих значень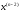 і відповідних управлінь
і відповідних управлінь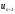 .
Ці обчислення дозволять визначити
умовно оптимальне управління
.
Ці обчислення дозволять визначити
умовно оптимальне управління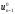 для кожного
для кожного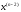 .
Кожне з таких управлінь спільно з вже
вибраним управлінням на останньому
кроці забезпечує максимальне значення
доходу на двох останніх кроках.
.
Кожне з таких управлінь спільно з вже
вибраним управлінням на останньому
кроці забезпечує максимальне значення
доходу на двох останніх кроках.
Послідовно здійснюючи описаний вище ітераційний процес, дійдемо, нарешті, до першого кроку. На цьому кроці нам відомо, в якому стані може знаходитися система. Тому вже не потрібно робити припущень про допустимі стани системи, а залишається тільки вибрати управління, яке є найкращим з врахуванням умовних оптимальних управлінь, вже прийнятих на всіх подальших кроках.
Таким
чином, в результаті послідовного
проходження всіх етапів від кінця до
початку визначаємо максимальне значення
виграшу за
 кроків і для кожного з них знаходимо
умовно оптимальне управління.
кроків і для кожного з них знаходимо
умовно оптимальне управління.
Щоб
знайти оптимальну стратегію управління,
тобто визначити шуканий розв’язок
задачі, потрібно тепер пройти всю
послідовність кроків, тільки цього разу
від початку до кінця. А саме: на першому
кроці в якості оптимального управління
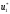 візьмемо знайдене умовне оптимальне
управління
візьмемо знайдене умовне оптимальне
управління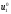 .
На другому кроці знайдемо стан
.
На другому кроці знайдемо стан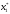 ,
у який переводить систему управління
,
у який переводить систему управління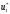 .
Цей стан визначає
знайдене умовне оптимальне управління
.
Цей стан визначає
знайдене умовне оптимальне управління
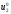 ,
яке тепер вважатимемо за оптимальне.
Знаючи
,
яке тепер вважатимемо за оптимальне.
Знаючи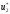 ,
знаходимо
,
знаходимо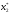 а
значить, визначаємо
а
значить, визначаємо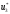 і так далі. В результаті цього знаходимо
розв’язок задачі, тобто максимально
можливий дохід і оптимальну стратегію
управління
і так далі. В результаті цього знаходимо
розв’язок задачі, тобто максимально
можливий дохід і оптимальну стратегію
управління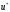 ,
що включає оптимальні управління на
окремих кроках:
,
що включає оптимальні управління на
окремих кроках: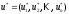 .
.
І. Теоретичні відомості.
Необхідність дослідження задач одновимірної оптимізації та розробка чисельних методів їх розв'язування обумовлена, по-перше, тим, що цей клас екстремальних задач є зручною моделлю для розробки і теоретичного дослідження ефективності методів багатовимірної оптимізації, а, по-друге, тим, що в багатьох методах відшукання екстремуму таких багатовимірних задач використовується одновимірний пошук.
Класичні
методи одновимірної мінімізації мають
досить обмежені застосування, оскільки
обчислення похідних в практичних задачах
не завжди можливе. Наприклад, значення
функції
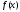 визначаються в результаті спостережень
чи деякого фізичного експерименту, і
отримати інформацію про її похідну
важко або взагалі неможливо в силу
недиференційовності функції, що
оптимізується. Але навіть у тих випадках,
коли похідну все ж таки вдається
обчислити, відшукання коренів рівняння
визначаються в результаті спостережень
чи деякого фізичного експерименту, і
отримати інформацію про її похідну
важко або взагалі неможливо в силу
недиференційовності функції, що
оптимізується. Але навіть у тих випадках,
коли похідну все ж таки вдається
обчислити, відшукання коренів рівняння і визначення інших точок, підозрілих
на екстремум, може бути пов'язане з
серйозними труднощами. Тому важливо
мати такі методи пошуку екстремуму, які
не вимагають обчислення похідних і є
більш зручними для реалізації на ЕОМ.
і визначення інших точок, підозрілих
на екстремум, може бути пов'язане з
серйозними труднощами. Тому важливо
мати такі методи пошуку екстремуму, які
не вимагають обчислення похідних і є
більш зручними для реалізації на ЕОМ.
Якщо
про цільову функцію
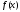 відомо лише те, що вона є неперервною
на заданій множині
відомо лише те, що вона є неперервною
на заданій множині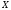 ,
то для знаходження точки глобального
мінімуму, взагалі кажучи, необхідно
досліджувати цю функцію в усіх точках
множини
,
то для знаходження точки глобального
мінімуму, взагалі кажучи, необхідно
досліджувати цю функцію в усіх точках
множини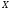 .
Але оскільки нас цікавить відшукання
деякого наближення точки мінімуму, то
для цього функцію досліджують у скінченній
кількості точок. Різні способи вибору
такої сукупності точок визначають і
різні методи одновимірної мінімізації.
.
Але оскільки нас цікавить відшукання
деякого наближення точки мінімуму, то
для цього функцію досліджують у скінченній
кількості точок. Різні способи вибору
такої сукупності точок визначають і
різні методи одновимірної мінімізації.
В математиці розроблено багато ефективних методів для розв'язування задач одновимірної мінімізації, орієнтованих на різні класи функцій, що зустрічаються при розв'язуванні прикладних задач.
Більшість
наближених методів одновимірної
мінімізації у процесі своєї реалізації
генерують послідовність відрізків
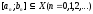 ,
що стягується до однієї з точок
,
що стягується до однієї з точок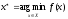 .
Однак, гарантувати приналежність точки
.
Однак, гарантувати приналежність точки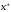 відрізку
відрізку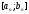 для деякого
для деякого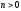 можна лише для певного класу функцій,
що мінімізуються на множині
можна лише для певного класу функцій,
що мінімізуються на множині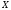 .
.
Далі розглянемо кілька найбільш поширених методів одновимірної мінімізації на класі функцій, у яких всі точки локального мінімуму є точками глобального мінімуму.
