
- •Кваліфікаційна робота
- •Зінченка Євгенія Анатолійовича
- •Розділ 1. Теоретичні відомості за темою дослідження
- •1.1. Метод функціональної підстановки
- •1.2. Застосування методу функціональної підстановки для спрощення виразів
- •1.3. Застосування методу функціональної підстановки для розв’язування рівнянь
- •Розділ 2. Приклади розв’язування задач методом функціональної підстановки
- •2.1. Рівняння, в яких заміна очевидна
- •2.2. Рівняння виду
- •2.4. Симетричні рівняння і обернені рівняння
- •2.5. Дробово-раціональні рівняння
- •2.6. Однорідні рівняння
- •Розділ 3. Охорона праці та безпека життєдіяльності в навчальних закладах
- •Висновки список використаних джерел
2.1. Рівняння, в яких заміна очевидна
Розглянемо наступні рівняння:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
Спосіб розв'язування:
1)
![]() .
.
Зведемо дане рівняння до
виду ![]() і,
зробивши підстановку
і,
зробивши підстановку![]() ,
розв'яжемо отримане рівняння
,
розв'яжемо отримане рівняння![]() .
Отримаємо
.
Отримаємо
![]() або
або
![]() .
Повернемося до
підстановки і розв'яжемо ще два рівняння:
.
Повернемося до
підстановки і розв'яжемо ще два рівняння:
a) ![]() ,
, ![]()
![]() або
або ![]() б)
б) ![]() ;
;
![]()
![]()
Відповідь: ![]() ;
; ![]() ;
; ![]()
![]()
2)
![]() .
Зробивши підстановку, отримаємо рівняння
.
Зробивши підстановку, отримаємо рівняння
![]() ,
розв’язок якого
,
розв’язок якого![]() або
або![]() .
Повертаючись до підстановки:
.
Повертаючись до підстановки:
a)
![]() ,
,![]() або
або![]() б)
б)![]() ,
,![]() розв’язків немає.
розв’язків немає.
Відповідь: ![]() ;
;![]()
3)
![]() .
.
Зробивши підстановку
![]() ,
розв'яжемо отримане рівняння
,
розв'яжемо отримане рівняння
![]() .
Отримаємо
.
Отримаємо ![]() або
або ![]() . Повернемося до
підстановки і розв'яжемо ще два рівняння:
. Повернемося до
підстановки і розв'яжемо ще два рівняння:
а)
![]() ,
,![]() або
або![]() б)
б)![]() ,
,![]() або
або![]() .
.
Відповідь: ![]() ;
;![]()
![]()
![]() .
.
4)
![]() .
.
Зведемо дане рівняння до
виду ![]() і,
Зробивши підстановку
і,
Зробивши підстановку![]() ,
розв'яжемо отримане рівняння
,
розв'яжемо отримане рівняння
![]() .
Отримаємо
.
Отримаємо ![]() або
або ![]() .
Повернемося до підстановки і розв'яжемо
ще два рівняння:
.
Повернемося до підстановки і розв'яжемо
ще два рівняння:
a) ![]() ,
,![]() або
або![]() б)
б)![]() ,
,![]()
Відповідь:
![]() ;
;![]() .
.
5)
![]() .
.
Зведемо дане рівняння до
виду ![]() і,
Зробивши підстановку
і,
Зробивши підстановку![]() ,
розв'яжемо отримане рівняння
,
розв'яжемо отримане рівняння
![]() .
Отримаємо
.
Отримаємо ![]() або
або ![]() .
Повернемося до підстановки і розв'яжемо
ще два рівняння:
.
Повернемося до підстановки і розв'яжемо
ще два рівняння:
a) ![]() ,
,![]() б)
б)![]() ,
,![]() .
.
Відповідь:
![]() .
.
2.2. Рівняння виду
при
![]() ,
,![]() ,
розв’язуються з використанням заміни:
,
розв’язуються з використанням заміни:
![]() .
.
Приклади:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
|
1)
Перепишемо дане рівняння у вигляді:
Так як
Підставляючи
або
Звідси знаходимо :
Рівняння вищезазначеного типу можна розв’язати і по іншому, перемноживши першу дужку з четвертою, а другу − з третьою, вводячи при цьому відповідну заміну. Розглянемо це на другому прикладі. |
|
2)
![]() .
.
Звернемо увагу, що сума
вільних членів першої і четвертої дужки
дорівнює сумі вільних членів другої і
третьої дужки. Перемноживши ці дужки,
отримаємо ![]() .
Зробимо заміну
.
Зробимо заміну ![]() ,
отримаємо рівняння
,
отримаємо рівняння ![]() ,
відкриємо дужки
,
відкриємо дужки ![]() ,
знайдемо корні за теоремою оберненої
до теореми Вієта
,
знайдемо корні за теоремою оберненої
до теореми Вієта ![]() або
або ![]() .
Повертаючись до заміни і розв'язуючи
ще два рівняння:
.
Повертаючись до заміни і розв'язуючи
ще два рівняння:
1)![]()
![]()
![]()
![]() ,
розв'язків немає.
,
розв'язків немає.
2)![]()
![]()
![]() або
або ![]()
Відповідь: ![]() ;
; ![]()
3)
![]() .
.
Cума вільних членів першої
і четвертої дужки дорівнює сумі вільних
членів другої і третьої дужки. Перемноживши
ці дужки, отримаємо ![]() .
Зробимо заміну
.
Зробимо заміну![]() ,
отримаємо рівняння
,
отримаємо рівняння![]() ,
відкриємо дужки
,
відкриємо дужки![]() ,
знаходимо корені,
,
знаходимо корені,![]() ,
,![]() .
Повертаючись до заміни і розв'язуючи
ще два рівняння:
.
Повертаючись до заміни і розв'язуючи
ще два рівняння:
а) ![]()
![]() ,
,![]() ,
,![]()
б)
![]()
![]()
![]() розв’язків немає.
розв’язків немає.
Відповідь: ![]() .
.
4)
![]() .
.
Аналогічно, перемноживши
відповідні дужки, отримаємо ![]() .
Зробимо заміну
.
Зробимо заміну![]() ,
отримаємо рівняння
,
отримаємо рівняння![]() ,
відкриємо дужки
,
відкриємо дужки![]() ,
знаходимо корені,
,
знаходимо корені,![]() ,
,![]() .
Повертаючись до заміни і розв'язуючи
ще два рівняння:
.
Повертаючись до заміни і розв'язуючи
ще два рівняння:
а) ![]()
![]() ,
,![]() ,
,![]()
б)
![]()
![]()
![]() ,
,![]() .
.
Відповідь: ![]() ;
;![]()
5)
![]()
Перемноживши відповідні
дужки, отримаємо ![]() .
Зробимо заміну
.
Зробимо заміну![]() ,
отримаємо рівняння
,
отримаємо рівняння![]() ,
знаходимо корені,
,
знаходимо корені,![]() ,
,![]() .
Повертаючись до заміни і розв'язуючи
ще два рівняння:
.
Повертаючись до заміни і розв'язуючи
ще два рівняння:
а) ![]()
![]() ,
,![]() або
або![]() .
.
б)
![]() ,
,![]()
![]() розв’язків
немає.
розв’язків
немає.
Відповідь: ![]() ;
;![]()
2.3. Рівняння виду ![]() .
.
Розглянемо розв’язування
рівнянь виду
![]() де
де![]()
![]() які зводиться до розв’язування сукупності
двох квадратних рівнянь за допомогою
заміни
які зводиться до розв’язування сукупності
двох квадратних рівнянь за допомогою
заміни![]()
Приклади:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
|
|
|
Відмітимо що,
![]() Перемноживши в лівій частині рівняння
першу і четверту дужки, а також другу і
третю, отримаємо:
Перемноживши в лівій частині рівняння
першу і четверту дужки, а також другу і
третю, отримаємо:
![]() .
.
Оскільки
![]() не є коренем даного рівняння, поділимо
обидві його частини на
не є коренем даного рівняння, поділимо
обидві його частини на![]() .
Отримаємо рівняння:
.
Отримаємо рівняння:
![]()
Рівносильне вихідному.
Зробимо заміну змінної
![]() Тоді отримаємо рівняння
Тоді отримаємо рівняння![]() або
або![]() ,
звідси
,
звідси![]()
![]() Таким чином, вихідне рівняння рівносильне
сукупності рівнянь:
Таким чином, вихідне рівняння рівносильне
сукупності рівнянь:
 або
або![]()
Розв’язуючи сукупність, отримуємо відповідь вихідного рівняння:
Відповідь: ![]()
2)
![]() .
.
Спочатку помножимо обидві
частини рівняння на ![]() ,
щоб замінити місцями доданки в другій
дужці. Отримаємо рівняння
,
щоб замінити місцями доданки в другій
дужці. Отримаємо рівняння
![]() .
Перемножимо ті дужки, в яких добуток
вільних членів однаковий, т. б. першу
дужку на четверту, а другу на третю.
Отримаємо
.
Перемножимо ті дужки, в яких добуток
вільних членів однаковий, т. б. першу
дужку на четверту, а другу на третю.
Отримаємо ![]() .
Оскільки
.
Оскільки ![]() не
є коренем даного рівняння, то поділимо
обидві частини рівняння на
не
є коренем даного рівняння, то поділимо
обидві частини рівняння на ![]() ;
отримаємо
;
отримаємо 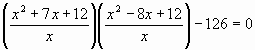 ;
перетворимо отриманий вираз
;
перетворимо отриманий вираз ![]() ;
зробимо заміну змінної
;
зробимо заміну змінної ![]() ;
і розв'яжемо рівняння
;
і розв'яжемо рівняння ![]() ;
; ![]()
![]()
![]() ;
; ![]() .
Повернемося до заміни і розв'яжемо ще
два рівняння:
.
Повернемося до заміни і розв'яжемо ще
два рівняння:
1) ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
2) ![]() ;
; ![]() ;
; ![]() ,
, ![]()
Відповідь: ![]() ;
; ![]() ;
; ![]()
3)
![]() .
.
Оскільки
![]() не є коренем даного рівняння, поділимо
обидві його частини на
не є коренем даного рівняння, поділимо
обидві його частини на![]() .
Отримаємо рівняння:
.
Отримаємо рівняння:
![]() ,
,
Рівносильне вихідному.
Зробимо заміну змінної
![]() Тоді отримаємо рівняння
Тоді отримаємо рівняння![]() або
або![]() ,
звідси
,
звідси![]()
![]() Таким чином, вихідне рівняння рівносильне
сукупності рівнянь:
Таким чином, вихідне рівняння рівносильне
сукупності рівнянь:
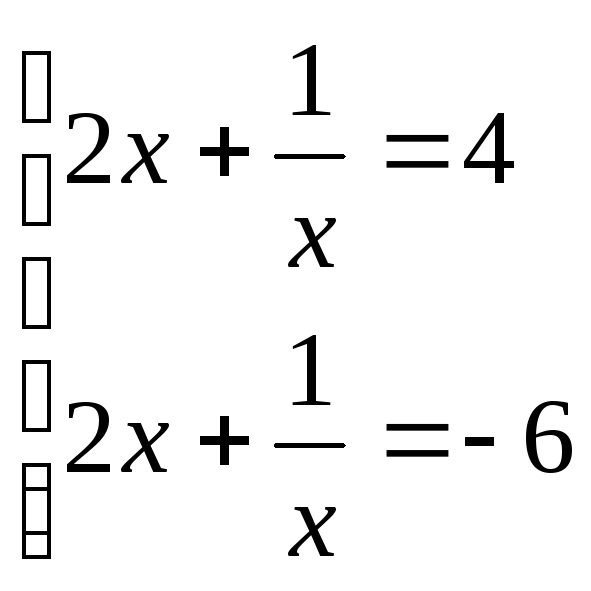 або
або![]()
Розв’язуючи сукупність, отримуємо відповідь вихідного рівняння:
Відповідь: ![]()
![]()
4)
![]() .
.
Зведемо дане рівняння до
виду
![]()
Оскільки
![]() ,
то перемножимо першу дужку з четвертою
та другу з третьою, отримаємо
,
то перемножимо першу дужку з четвертою
та другу з третьою, отримаємо![]()
![]() не є коренем даного рівняння, поділимо
обидві його частини на
не є коренем даного рівняння, поділимо
обидві його частини на![]() .
.
![]()
Зробимо заміну змінної
![]() Тоді отримаємо рівняння
Тоді отримаємо рівняння![]() або
або![]() ,
звідси
,
звідси![]()
![]() Таким чином, вихідне рівняння рівносильне
сукупності рівнянь:
Таким чином, вихідне рівняння рівносильне
сукупності рівнянь:
 або
або![]()
Розв’язуючи сукупність, отримуємо відповідь вихідного рівняння:
Відповідь: ![]()
![]()
![]()
5)
![]()
Розв’язуючи аналогічно попереднім прикладам отримуємо:
![]()
![]()
![]() .
.
Вводимо заміну
![]() ,
,![]() звідки
звідки![]() знаходимо
знаходимо![]()
![]() .
.
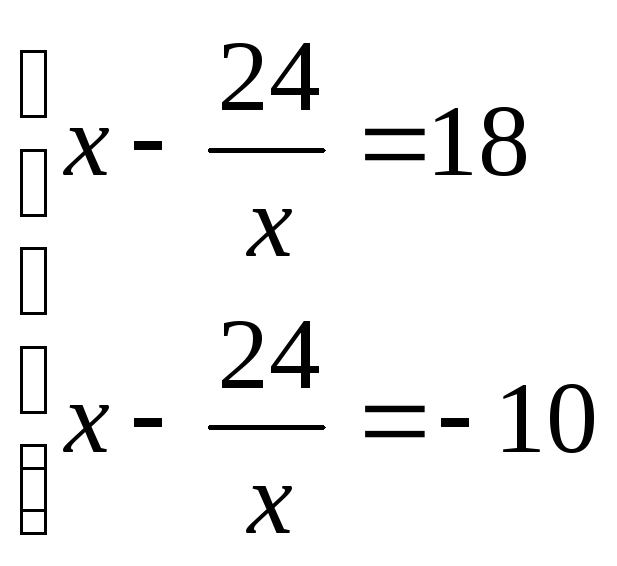 або
або![]()
Розв’язуючи сукупність, отримуємо відповідь вихідного рівняння:
Відповідь: ![]()
![]()
![]()
