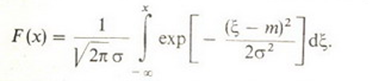9 Корреляционный анализ. Корреляционная функция, ее свойства. Вычисление корреляционной функции одиночного импульса и периодического сигнала

Наряду со спектральным анализом корреляционный анализ играет большую роль в теории сигналов. Его смысл состоит в измерении степени сходства (различия) сигналов. Для этого служит корреляционная ф-ция.

КФ представляет собой интеграл от произведения двух копий сигнала, сдвинутых друг отн. друга на время .

Чем больше значение КФ, тем сильнее сходство. КФ обладает следующими свойствами:

1. Значение КФ при равно энергии сигнала (интегралу от его квадрата)

2. Является четной функцией

3. Значение КФ при является максимально возможным.

4. С ростом абс. значения КФ сигнала с конечной энергией затухает

5. Если сигнал является ф-цией напряжения от времени, то размерность его КФ []

В случае периодического сигнала (с периодом Т) КФ вычисляют, усредняя произведение сдвинутых копий в пределах одного периода:

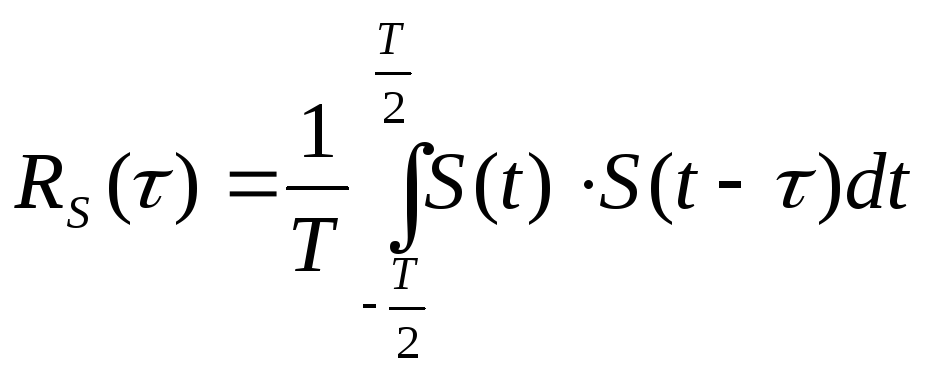
Набор свойств такой КФ изменяется:

1. Значение КФ при равно средней мощности сигнала

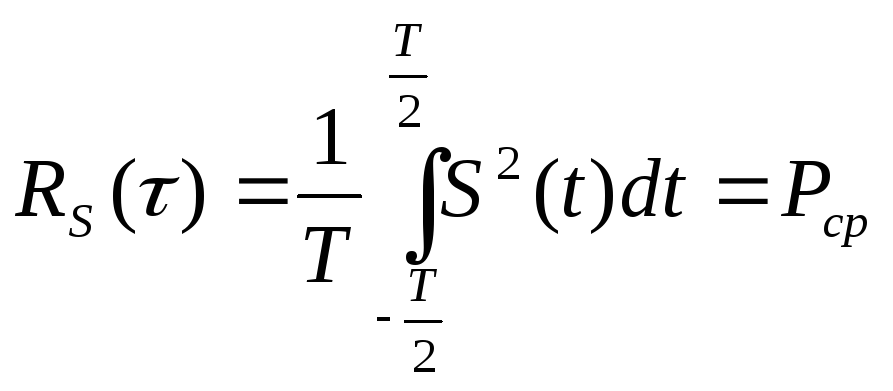
2. Свойство четности сохраняется.

3. Значение КФ при является максимально возможным.

4. КФ является периодической ф-цией (с тем же периодом, что и сигнал)

5. Если сигнал не содержит дельта-функций, то его КФ непрерывна.

6. Если сигнал является зависимостью U(t), то размерность КФ []

КФ гармонического сигнала является гармонической ф-цией, которая не зависит от начальной фазы сигнала.

10 Взаимная корреляционная функция, ее свойства. Вычисление взаимной корреляционной функции сигналов

Взаимная корреляционная функция (ВКФ)- функция, показывающая степень сходства для сдвинутых во времени 2-ух различных сигналов.

Общий вид:

Для примера вычислим ВКФ 2-ух функций:

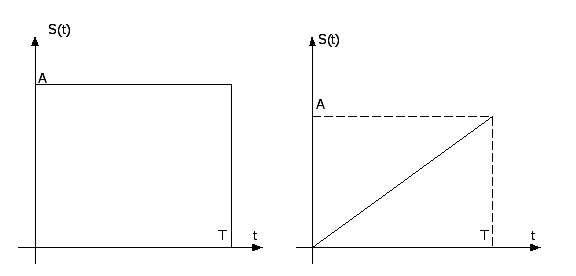
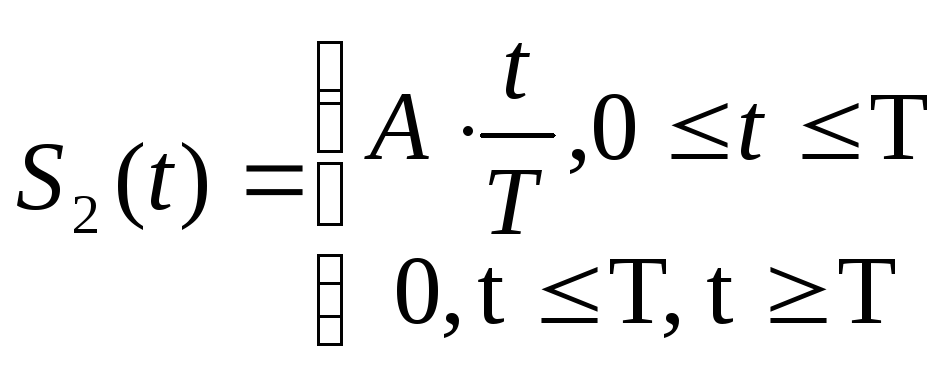
При

При

При

Объединяя результаты, можно записать:

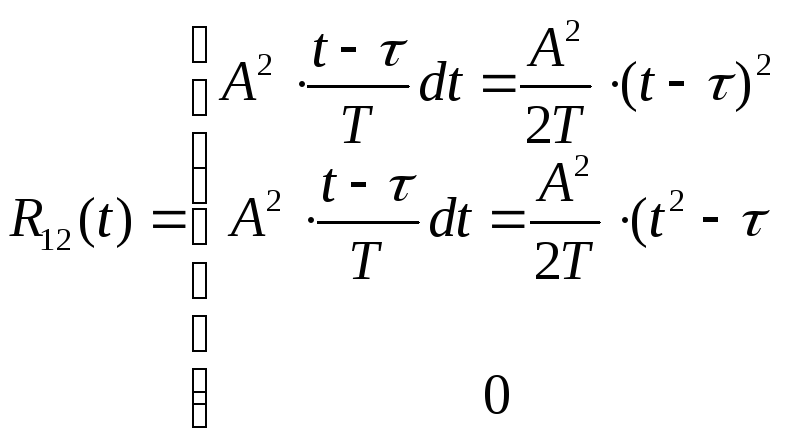
Свойства ВКФ:

1)

2)

3)

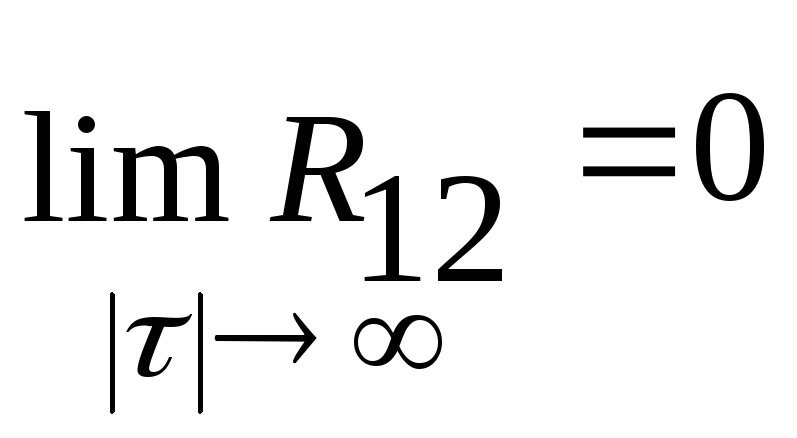
4) Если функции S₁(t) и S₂(t) не содержат дельта-функций, то их ВКФ не может иметь разрывов.

5) Если в качестве сигнала выступает функция U(t), то размерность ВКФ

11 Случайные процессы. Реализация случайного процесса. Законы распределения случайных процессов

_{Иногда на практике приходится иметь дело с явлениями, протекание которых во времени непредсказуемо и в каждый момент времени описывается случайной величиной. Такие явления называются случайными процессами. Случайным процессом называется функция ζ(t) неслучайного аргумента t (как правило, времени), которая при каждом фиксированном значении аргумента является случайной величиной. Например, температура в течение суток, регистрируемая самописцем. Значения, принимаемые процессом ζ(t) в определенные моменты времени называются состояниями, а множество всех состояний – фазовым пространством случайного процесса. В зависимости от количества возможных состояний случайного процесса его фазовое пространство может быть дискретным или непрерывным. Если случайный процесс может изменять свое состояние лишь в определенные моменты времени, то такой процесс называется случайным процессом с дискретным временем; а если в произвольные, то – процессом с непрерывным временем.}

Случайный процесс ζ(t) называется стационарным, если распределение вероятностей его возможных состояний не изменяется во времени. Например, при ежесекундном подбрасывании игральной кости распределение вероятностей состояний соответствующего случайного процесса (рис.44, б) не зависит (не изменяется) от времени (при этом все состояния ζ(t) равновозможны). В противоположность этому, случайный процесс, характеризующий температуру окружающей среды, не является стационарным, т.к. для лета характерны более высокие температуры, чем для зимы.

Распределение вероятностей состояний стационарного случайного процесса называется стационарным распределением.

Существуют различные законы распределения среди них Равномерное, Гаусовское (нормальное)

Равномерное: пусть некторая случ величина х может принимать значения х₁<=x<=x₂ тогда плотность вероятности

P(x)=система(0 при x<x₁;1/(x₂-x₁) при х1<=x<=x₂; 0 при х>х₂)

Функцию распределения найдем путем интегрирования

F(x)= система(0 при x<x₁;(x-x₁)/(x₂-x₁) при х1<=x<=x₂; 1 при x>x₂)

Гауссово (нормальное) распределение. В теории случайных сигналов фундаментальное значение имеет гауссова плотность вероятности

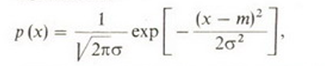
содержащая два числовых параметра . График данной функции представляет собой колоколообразную кривую с единственным максимумом в точке.

Непосредственным вычислением можно убедиться, что параметры гауссова распределения имеют смысл соответственно математического ожидания и дисперсии:

Функция распределения гауссовой случайной величины