
- •Раздел 1Статика.
- •Вопрос 1.1 Введение в теоретическую механику.
- •Вопрос 1.2 Механические связи и их реакции
- •Вопрос 1.3 Проекция силы на ось
- •Вопрос 1.4 Момент силы относительно точки
- •Вопрос 1.5 Пара сил
- •Вопрос 1.6 Центр тяжести твердого тела
- •Вопрос 2.1 Уравнения равновесия для тела, находящегося под действием плоской системы сил.
- •Вопрос 2.2 Анализ равновесия систем тел
- •Вопрос 2.3 Уравнения равновесия для пространственной системы сил
- •Вопрос 2.4 Реакции связей для пространственной системы сил
- •Вопрос 3.1Понятие о ферме
- •Вопрос 3.2 Определение внутренних сил фермы способом вырезания узлов
- •Вопрос 3.3Расчет плоских ферм способом сечений
- •Раздел 2Кинематика
- •Вопрос 4.1 Способы описания движения точки.
- •Вопрос 4.2 Определение кинематических параметров движения точки.
- •Вопрос 5.1 Основные понятия и определения
- •Вопрос 5.2 Скорость и ускорение точки на вращающемся теле.
- •Вопрос 5.3 Преобразование простейших движений тела.
- •Вопрос 5.4 Плоскопараллельное движение
- •Плоскопараллельным(плоским) называется такое движение тела, при котором все его точки перемещаются в параллельных плоскостях.
- •Вопрос 5.5 Расчет скоростей точек с использованием мгновенного центра скоростей.
- •Вопрос 6.1 Ускорение точек на плоско движущемся теле.
- •Вопрос 6.2Скорость и ускорение точки при сложном движении.
- •Раздел 3 Динамика.
- •Вопрос 7.1 Законы динамики материальной точки
- •Вопрос 7.2 Задачи динамики материальной точки
- •Вопрос 7.3 Теоремы динамики материальной точки
- •Вопрос 7.4 Работа силы
- •Вопрос 8.1 Основные понятия теории механических колебаний.
- •Вопрос 8.2Свободные колебания материальной точки
- •Вопрос 8.3 Вынужденные колебания материальной точки.
- •Вопрос 8.4 Замена системы пружин эквивалентной пружиной
- •Вопрос 9.1Теорема о движении центра масс материальной системы.
- •Вопрос 9.2Динамические уравнения движения твердого тела.
- •Вопрос 9.3 Динамические уравнения плоского движения
- •Вопрос 9.4 Теоремы об изменении количества движения и момента количества движения материальной системы.
- •Вопрос 9.5Теорема об изменении кинетической энергии материальной системы.
- •Вопрос 10.1 Принцип возможных перемещений
- •Вопрос 10.2 Сила инерции.
- •Вопрос 10.3 Принцип Даламбера и общее уравнение динамики
Вопрос 1.3 Проекция силы на ось
 Проекцией
силы на ось
называется направленный отрезок на
оси, заключенный между перпендикулярами,
опущенными из начала и конца вектора
силы на ось (рисунок 1.9).
Проекцией
силы на ось
называется направленный отрезок на
оси, заключенный между перпендикулярами,
опущенными из начала и конца вектора
силы на ось (рисунок 1.9).
З
Рисунок 1.9
На рисунке 1.10 показаны случаи нахождения проекций сил на ось координат.

Рисунок 1.10![]() ;
;
![]() ;
;![]() ;
;![]() .
.
Вопрос 1.4 Момент силы относительно точки
Моментом силы относительно точки называется произведение модуля силы на ее плечо:
![]()
 .
.
Плечо силы – это длина перпендикуляра, опущенного из точки, относительно которой определяется момент, на линию действия силы.
Е
Рисунок 1.11![]() относительно точки А (рисунок 1.11)
соответственно равны:
относительно точки А (рисунок 1.11)
соответственно равны:
![]() В
случаях, когда нахождение плеча
затруднено, для вычисления момента силы
относительно точки целесообразно
использовать теорему
Вариньона: момент равнодействующей
силы относительно некоторой точки равен
алгебраической сумме моментов сил,
составляющих систему, относительно той
же точки:
В
случаях, когда нахождение плеча
затруднено, для вычисления момента силы
относительно точки целесообразно
использовать теорему
Вариньона: момент равнодействующей
силы относительно некоторой точки равен
алгебраической сумме моментов сил,
составляющих систему, относительно той
же точки:
![]() .
.
П ри
решении задач для нахождения момента
силы
ри
решении задач для нахождения момента
силы![]() относительно точки с помощью теоремы
Вариньона силу раскладывают на
составляющие, моменты которых относительно
рассматриваемой точки легко определяются.
Затем искомый момент получают как
алгебраическую сумму моментов
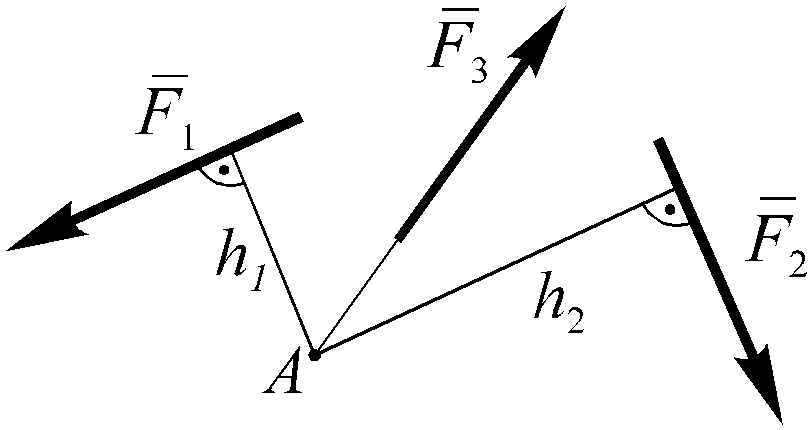
составляющих. Например, для схемы,
изображенной на рисунке 1.12, имеем
относительно точки с помощью теоремы
Вариньона силу раскладывают на
составляющие, моменты которых относительно
рассматриваемой точки легко определяются.
Затем искомый момент получают как
алгебраическую сумму моментов
составляющих. Например, для схемы,
изображенной на рисунке 1.12, имеем
Рисунок 1.12![]()
Вопрос 1.5 Пара сил
Пара сил – это система двух равных по модулю, параллельных и противоположных по направлению сил.
И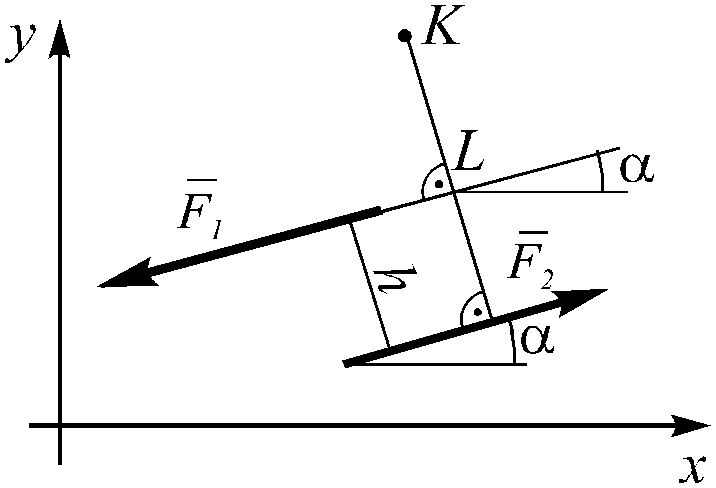 з
рисунка 1.13 видно, что сумма проекций
сил пары на оси координат всегда равна
нулю:
з
рисунка 1.13 видно, что сумма проекций
сил пары на оси координат всегда равна
нулю:
![]()
![]()
Н
Рисунок 1.13
![]()
Из полученного выражения видно, что результат не зависит от расстояния KL (следовательно, от положения точки K), а определяется только расстоянием h. Расстояние h между линиями действия сил пары называют плечом пары.
Момент пары считается положительным, если она стремится повернуть тело при действии против хода часовой стрелки, и отрицательным – при действии по ходу часовой стрелки.
На
расчетных схемах для обозначения пар
сил применяются символы
![]() либо
либо![]() .
.
Вопрос 1.6 Центр тяжести твердого тела
Центром тяжести тела называется точка приложения его силы тяжести.
Для нахождения положения центра тяжести используют следующие способы:
1 Метод симметрии. У однородного тела, имеющего плоскость, ось или центр симметрии, центр тяжести находится соответственно в плоскости, на оси или в центре симметрии.
2 Метод разбиения на части. Если тело имеет сложную форму, его разбивают на части, положения центров тяжести которых известны. В таком случае положения центров тяжести тела определяют с использованием следующих выражений.
Координаты центра тяжести объемного тела постоянной плотности находятся по формулам
![]() ;
;
![]() ;
;![]() ,
,
где
![]() –
координаты центров тяжести элементарных
частей,
–
координаты центров тяжести элементарных
частей,
![]() –объем
i-й
части.
–объем
i-й
части.
Если тело представляет собой однородную пластину постоянной толщины, то координаты ее центра тяжести
![]() ;
;
![]() ,
,
где
![]() –
площадьi-го
элемента.
–
площадьi-го
элемента.
Для стержневых конструкций, образованных стержнями одинаковой плотности и постоянного поперечного сечения, координаты центра тяжести определяют по формулам
![]() ;
;
![]() ;
;![]() ,
,
где
![]() –
длина элемента линии.
–
длина элемента линии.
3 Метод отрицательных сил тяжести. При нахождении положения центра тяжести тела, имеющего вырезы, полости, отверстия и т. п., используют метод разбиения на части, причем считается, что полости (их площади, объемы) имеют отрицательный вес.
Лекция 2 Уравнения равновесия.
(2 часа, 1 семестр, 1 курс)
