Вопрос 8.2Свободные колебания материальной точки

Динамическое уравнение свободных колебаний материальной точки может быть приведено к виду

,

Каноническая форма уравнения свободных колебаний:

,

где .

Решение данного уравнения зависит от соотношения величин nиk.

1) Отсутствие вязкого сопротивления (n= 0). В этом случае решение уравнения (2.1) имеет вид

,

то есть в данном случае точка совершает гармонические колебания.

Величина A, равная наибольшему отклонению точки от положения равновесия, называетсяамплитудой колебаний. Величина, являющаяся аргументом функции синус (или косинус), называется фазой колебаний. Величина₀, равная значению фазы колебаний приt= 0, называетсяначальной фазой.

Значения величин Aи₀при свободных колебаниях определяются начальными условиями. В качестве начальных условий выступают координатаx₀и скоростьv₀() материальной точки в начальный момент времени (t= 0). Величинаkназываетсякруговой частотой колебаний. Промежуток времениT, в течение которого точка совершает одно полное колебание, называетсяпериодом колебаний. Величина, обратная периоду и определяющая число колебаний за 1 с, называетсячастотой колебаний. По истечении промежутка времени, равного периоду колебанийT, фазаизменяется на 2. Следовательно, период колебаний связан с круговой частотой. Циклическая частота связана с круговой следующим образом:.

2) Случай малых сопротивлений (n<k). При этом решение уравнения (2.1) имеет вид

.

В этом случае точка совершает затухающие колебания. Их период больше периода колебаний, происходящих при отсутствии вязкого сопротивления, и определяется по формуле

.

Амплитуда затухающих колебаний изменяется со временем . Отношение двух соседних максимумов отклонения точки от положения равновесия при затухающих колебаниях называетсядекрементом колебаний, и определяется соотношением

.

Модуль логарифма декремента затухания называетсялогарифмическим декрементом колебаний

.

3) Случай «равных» сопротивлений (n=k). При этом

.

Здесь C₁,C₂– постоянные, определяемые из начальных условий.

4) Случай больших сопротивлений (n>k). При этом

.

В этом случае колебания отсутствуют, и точка возвращается в положение равновесия.

Вопрос 8.3 Вынужденные колебания материальной точки.

Если материальная точка совершает колебания под действием гармонической силы , то динамическое уравнение движения такой точки в канонической форме имеет вид

.

Здесь . Решение приведенного уравнения представляет собой сумму, гдеx₀– общее решение однородного уравнения;x₁– частное решение неоднородного уравнения. Решениеx₁определяется следующим образом:

,

где .

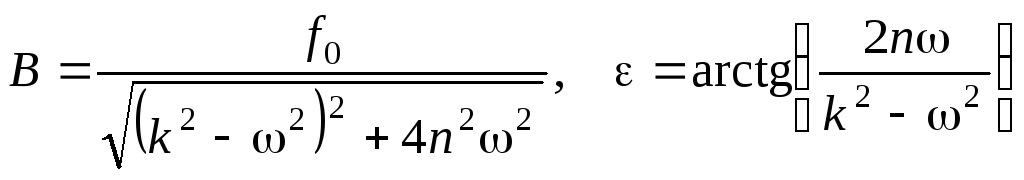Следовательно, общее решение неоднородного уравнения (2.6) в случае малых сопротивлений (n<k) можно записать в виде

.

Значение Bназывают амплитудой вынужденных колебаний; значение ε – отклонение фазы вынужденных колебаний от фазы вынуждающей силы.

Резонансомназывают явление резкого увеличения амплитуды вынужденных колебаний при сближении частоты вынуждающей силыс частотой собственных колебанийk. Частоту вынуждающей силы, соответствующую резонансу, называют резонансной частотой_р. Можно показать, что значение частоты_ропределяется следующим образом:

.