3. Сложение одинаково направленных гармонических колебаний одинаковой частоты. (Дать понятие вектора амплитуды и векторной диаграммы. С помощью векторной диаграммы найти амплитуду и начальную фазу результирующего колебания).

Контрольные вопросы

1.Что такое период колебаний?

2.Как связана частота колебаний с циклической частотой колебаний?

3.Является ли обычная пружина определенной (не равной нулю) массы пружинным маятником?

4.Какие величины, характеризующие гармонические колебания материальной точки, зависят от времени по законам косинуса и синуса?

5.Как движется материальная точка, одновременно участвующая в двух колебаниях одного направления и одинаковой частоты? Может ли она оставаться в покое?

Лекция 2 «Затухающие и вынужденные колебания»

План лекции

1.Затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решение. (Получить дифференциальное уравнение затухающих колебаний в случае, когда сила сопротивления пропорциональна величине скорости. Свести это уравнение к виду дифференциального уравнения гармонических колебаний, записать его решение и построить график x(t) .)

2.Характеристики затухающих колебаний. (Дать определения и найти выражения для логарифмического декремента затухания, времени релаксации, добротности).

3.Вынужденные колебания. (Получить дифференциальное уравнение вынужденных колебаний в случае гармонической вынуждающей силы. Найти его общее решение с помощью векторной диаграммы).

4.Механический резонанс. (Исследовать зависимость амплитуды и начальной фазы вынужденных колебаний от частоты вынуждающей силы. Дать определение механического резонанса, построить резонансные кривые.)

Контрольные вопросы

1.Совпадают ли частоты незатухающих и затухающих колебаний механической системы?

2.По какому закону уменьшается амплитуда затухающих колебаний?

3.Во сколько раз уменьшается амплитуда затухающих колебаний за время релаксации?

241

4. Изменяется ли с течением времени амплитуда вынужденных колеба-

ний?

5. Чему равна амплитуда вынужденных колебаний при резонансе, если сопротивление в системе отсутствует?

Вопросы для самоконтроля

Iуровень (репродуктивный)

1.Какой процесс называется механическими колебаниями?

2.Что такое период колебаний?

3.Какие колебания называются гармоническими?

4.Что такое амплитуда колебаний, фаза колебаний, циклическая частота колебаний?

5.Связь между периодом и циклической частотой колебаний.

6.Пружинный маятник. Квазиупругая сила.

7.Дифференциальное уравнение гармонических колебаний.

8.Зависимость скорости и ускорения колеблющейся точки от времени.

9.Чему равна механическая энергия материальной точки, совершающей гармонические колебания?

10.Что такое вектор амплитуды гармонического колебания?

11.Амплитуда и начальная фаза колебания, полученного в результате сложения двух колебаний одинакового направления и одинаковой частоты.

12.Как движется материальная точка, участвующая в двух взаимно перпендикулярных колебаниях одинаковой частоты?

13.Что такое биения? В каком случае материальная точка совершает

биения?

14.Дифференциальное уравнение затухающих колебаний, коэффициент затухания.

15.Зависимость амплитуды затухающих колебаний от времени.

16.Циклическая частота затухающих колебаний.

17.Логарифмический декремент затухания, время релаксации, добротность колеблющейся системы.

18.Какие колебания называются вынужденными?

19.Дифференциальное уравнение вынужденных колебаний.

20.Частота, амплитуда и начальная фаза вынужденных колебаний.

21.Что такое механический резонанс? Чему равна резонансная частота?

22.Что такое физический маятник? Формула периода его колебаний.

23.Что такое математический маятник? Формула периода его колеба-

ний.

IIуровень (продуктивный)

1.Найти связь между периодом и циклической частотой гармонических колебаний.

242

2.На примере пружинного маятника найти выражение для квазиупругой силы. То же самое для математического маятника.

3.Получить дифференциальное уравнение гармонических колебаний. Записать его решение и проверить его правильность.

4.С помощью векторной диаграммы найти результат сложения двух гармонических колебаний одного направления и одинаковой частоты.

5.Найти траекторию движения материальной точки, одновременно участвующей в двух взаимно перпендикулярных колебаниях одинаковой частоты.

6.Рассмотреть сложение двух гармонических колебаний одного направления и близких частот (биения). Получить выражение для результирующего смещения от положения равновесия. Найти частоту биения.

7.Получить дифференциальное уравнение затухающих колебаний. Найти его решение.

8.Найти зависимость между логарифмическим декрементом затухания и периодом колебаний, временем релаксации и коэффициентом затухания.

9.Получить дифференциальное уравнение вынужденных колебаний в случае гармонической вынуждающей силы. Найти его общее решение с помощью векторной диаграммы.

10.Исследовать зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы. Найти выражение для резонансной частоты.

11.Получить формулу периода колебаний физического маятника.

Шуровень (творческий)

1.Показать, что если ось подвеса физического маятника перенести в его центр колебаний, то период колебаний не изменится.

2.Найти частоту изменения кинетической энергии материальной точки, колеблющейся по закону: x = a cos(ω0t + α) .

3.Найти частоту изменения потенциальной энергии материальной точки, колеблющейся по закону: x = Asin(ω0t + α) .

4.Найти зависимость от времени механической энергии материальной точки, совершающей затухающие колебания.

243

Задача 2 (уровень 2)

Материальная точка массой m =10 г совершает гармонические колебания с частотой ν = 0,2 Гц. Амплитуда колебаний равна 5 см. Определить: 1) максимальную силу, действующую на точку; 2) полную энергию колеблющейся точки.

245

Аудиторные задачи

Задача 1 (уровень 1).

Гармонические колебания с амплитудой A = 4 см и периодом T = 2с. Написать уравнение движения точки, если ее движение начинается из поло-

жения x0 = 2 см. [ x = 0,04 cos (πt +π3 ) м.]

Задача 2 (уровень 2).

Скорость материальной точки, совершающей гармонические колебания задается уравнением υ(t) = −6sin 2πt . Записать зависимость смещения этой

точки от времени [ x(t) = π3 cos 2πt .]

4.2.2 Сложение одинаково направленных гармонических колебаний одинаковой частоты. Биения. Сложение взаимно перпендикулярных колебаний одинаковой частоты

Примеры решения задач

Задача 1 (уровень 1)

Складываются два колебания одинакового направления, выраженные уравнениями:

Построить векторную диаграмму сложения этих колебаний и написать уравнение результирующего колебания.

Дано:

x1 = A1 cos 2Tπ(t + τ1) x2 = A2 cos 2Tπ

246

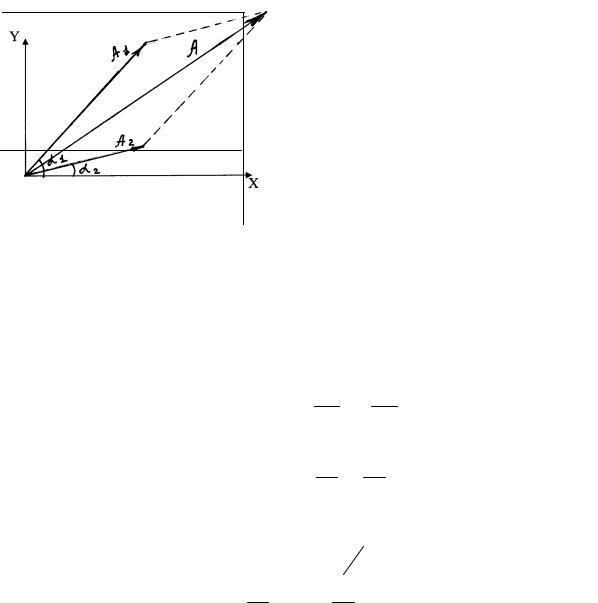
A1 = 3 см;

A2 = 2 см;

τ1 = 1/6 с;

τ2 = 1/3 с;

T= 2с.

x= f (t) — ?

Рис. 4.14

Решение

Для построения векторной диаграммы сложения двух колебаний одного направления надо фиксировать какой-либо момент времени. Обычно векторную диаграмму строят для момента времени t = 0. Преобразовав оба уравнения к форме: x = Acos(ω0t +ϕ) ,

получим:

x1 = A1 cos( 2Tπ t + 2Tπ τ1 ) ,

x2 = A2 cos(2Tπt + 2Tπ τ2 ) .

Отсюда видно, что оба складываемых гармонических колебания имеют одинаковую циклическую частоту ω0 = 2πT . Начальные фазы 1-го и 2-го ко-

лебаний соответственно ϕ1 = 2Tπ τ1,ϕ2 = 2Tπ τ2 .

Произведем вычисления:

зультирующие колебания будут происходить с той же частотойr и амплитудой A , равной геометрической сумме векторов амплитуд A1 и A2 :

A = A1 + A2 .

247

Согласно теореме косинусов

A = A12 + A22 +2A1A2 cos(ϕ2 −ϕ1) .

Начальную фазу результирующего колебания можно определить непосредственно из векторной диаграммы (рис. 4.14):

ϕ = arctg A1 sin ϕ1 + A2 sin ϕ2 . A1 cosϕ1 + A2 cosϕ2

Произведем вычисления:

Задача 2 (уровень 1).

Написать уравнение результирующего колебания, получающегося в результате сложения двух взаимно перпендикулярных колебаний с одинаковой

частотой ν1 = ν2 = 5 Гц и с одинаковой начальной фазой ϕ1 = ϕ2 = π3 . Амплитуды колебаний равны A1 = 0 ,1 м и A2 = 0,05м.

Решение

При сложении двух взаимно перпендикулярных колебаний одинакового периода уравнение траектории результирующего колебания имеет вид:

Так как у нас ϕ2 −ϕ1 = 0 , то уравнение (1) примет вид:

x2 + y2 − 2xy =

A12 A22 A1A2 0 ,

248

уравнение прямой линии. Таким образом, результирующее колебание будет происходить по прямой линии. Угол наклона прямой найдется из уравнения

ния имеет вид l =11,2sin(10πt + π3) см.

Аудиторные задачи

Задача 1(уровень 1).

Разность фаз двух одинаково направленных гармонических колебаний одинакового периода 4 с и одинаковой амплитуды 5 см составляет π4 . Напи-

сать уравнение движения, получающегося в результате сложения этих колебаний, если начальная фаза одного из них равна нулю.

[ x = 9,24 cos ( π2 t +π8 ) см].

Задача 2 (уровень 1)

Результирующее колебание, получающееся при сложении двух гармонических колебаний одного направления близких частот, описывается уравнением вида x = Acost cos45t (t — в секундах). Определить:

1)циклические частоты складываемых колебаний;

2)период биений результирующего колебания. [1) ω1 = 46с-1; ω2 = 45с-1;

2)T = 6,28с ].

4.2.3Пружинный, математический и физический маятники.

Примеры решения задач

Задача 1 (уровень 1)

Два математических маятника, длины которых отличаются на l , совершают за одно и то же время один n1 = 10 колебаний, другой n2 = 6 колеба-

ний. Определить длины маятников l1 и l2 .

249

На стержне длиной l = 30 см укреплены два грузика: один в середине стержня, другой — на одном из его концов. Стержень с грузиками колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину Lïð и период T гармонических колебаний.

На горизонтальной пружине жесткостью 800 н/м укреплен шар массой 4 кг, лежащий на гладком столе, по которому он может скользить без трения. Пуля массой 10 г, летящая с горизонтальной скоростью 600 м/с и имеющая в момент удара скорость, направленную вдоль оси пружины, попала в шар и застряла в нем. Пренебрегая массой пружины и сопротивлением воздуха, определить: 1) амплитуду колебаний шара; 2) период колебаний шара [1) 10 см; 2) 0,419 с.]

251

4.2.4 Затухающие колебания. Вынужденные колебания

Примеры решения задач

Задача 1 (уровень 1)

Математический маятник, выведенный из положения равновесия, отклонился при первом колебании на расстояние A1 = 3см, а при втором

A2 = 2,5 см. Время релаксации τ = 11 с. Определить длину маятника.

декремент затухания d , коэффициент затухания β, период этих колебаний T , если амплитуда уменьшилась в n = 16 раз на протяжении N = 100 коле-

252

A e−βt

n = A0e0−β(t +t1 ) = eβt1 .

Прологарифмируем данное выражение:

ln n =βt1; логарифмический декремент затухания d =βT , следователь-

2) Период затухающих колебаний определяется по формуле:

Решая совместно эти уравнения, получим:

3) Коэффициент затухания:

β = 00,,027729 с-1.

Ответ: d= 0,027; T = 0,789 с; β = 0,035 с-1.

Аудиторная задача (уровень 2)

Определить амплитуду вынужденных колебаний груза массой 0,1 кг на пружине с коэффициентом жесткости 10 Н/м, если на груз действует вертикальная вынуждающая гармоническая сила с амплитудой 1,5 Н и частотой, в два раза большей собственной частоты колебаний груза на пружине. Коэффициент затухания 0,4 с-1. [А = 5,0 см.]

253

4.3 МАТЕРИАЛЫ К ЛАБОРАТОРНЫМ ЗАНЯТИЯМ

Лабораторная работа «Определение момента инерции физического маятника»

Основные понятия, определения, законы и формулы динамики вращательного движения твердого тела

1. Гармонические колебания — это такое движение материальной точки или тела, при котором смещение от положения равновесия зависит от времени по закону синуса или косинуса, а именно:

x = Asin(ω0t +α) , x = Acos(ω0t +α) ,

где величины A, ω0 , α−постоянны.

2. Скоростьматериальнойточки, совершающейгармоническиеколебания,

3. Ускорение материальной точки, совершающей гармонические колебания,

a= •x• = ddυt = −Aω02 cos(ω0t +α) .

4.Гармонические колебания совершаются под действием квазиупру-

гой силы

f x= −kx ,

направленной против смещения, т. е. в положение равновесия, и пропорциональной величине смещения.

5. Смещение x как функция времени является решением дифференци-

ального уравнения гармонических колебаний:

••

x+ ω02 x = 0 .

6. Пружинный маятник, состоящий из упругой невесомой пружины жесткостью k , к концу которой прикреплена материальная точка массой m , совершает гармонические колебания, период которых

T = 2π mk .

254

7. Физический маятник — это абсолютно твердое тело произвольной формы, подвешенное на горизонтальной оси, не проходящей через центр масс тела. Период колебаний физического маятника

T = 2π mgI L ,

где I — момент инерции маятника относительно оси подвеса, L — расстояние от оси подвеса до центра масс маятника.

8. Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити. Период колебаний математического маятника

T = 2π gl ,

где l — длина нити, g — ускорение свободного падения.

9. Полная механическая энергия материальной точки, совершающей гармонические колебания, складывается из кинетической и потенциальной энергии;

Wìåõ = kA22 .

10. Реальные свободные колебания являются затухающими. Если величина силы сопротивления пропорциональна скорости, то при затухающих колебаниях смещение от положения равновесия зависит от времени по закону:

x = A0e−βt cos(ωt +α) ,

где A = A0e−βt амплитуда затухающих колебаний,

β — коэффициент затухания.

11. Логарифмическим декрементом затухания называется натуральный логарифм отношения предыдущей амплитуды к последующей амплитуде:

d = ln A(t +T ) .

Логарифмичесий декремент затухания связан с периодом колебаний:

d=βT .

12.Время релаксации — это промежуток времени, в течение которого амплитуда колебаний уменьшается в e раз:

255

τ = β1 .

Если в течение времени релаксации τ происходит Ne колебаний, то

d = 1 .

Ne

13. Добротностью колеблющейся системы называется безразмерная величина Q , равная произведению 2π и отношения энергии колеблющейся

системы в некоторый момент времени к потере энергии за один период колебаний:

Q = 2πW (t) −W (t +T ) .

При малых значениях логарифмического коэффициента затухания

Q = dπ .

14. Вынужденные колебания — это колебания, происходящие при действии внешней периодической силы. Они происходят с частотой этой вынуждающей силы; амплитуда вынужденных колебаний зависит от частоты вынуждающей силы по закону:

где F0 — амплитуда вынуждающей силы,

Ω — циклическая частота вынуждающей силы.

15. Механический резонанс — это явление резкого увеличения амплитуды вынужденных колебаний при приближении частоты вынуждающей си-

лы к собственной частоте колебаний системы ω0 . Резонансная частота

Ωðåç = ω02 − 2β2 .

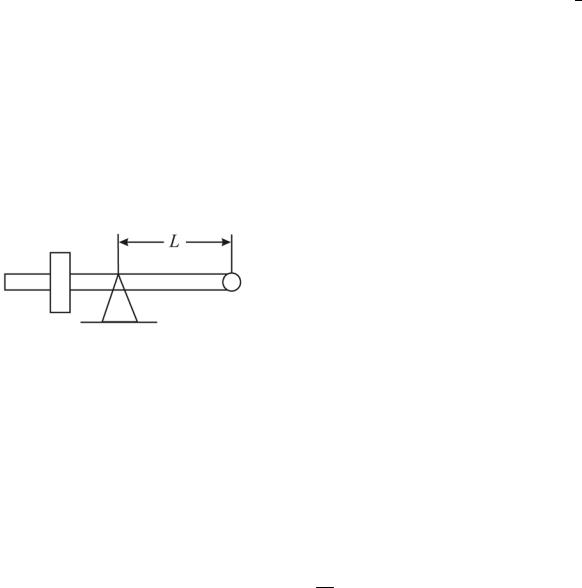
Описание лабораторной работы

Как известно, момент инерции тела вычисляется с помощью суммирования или (более точно) интегрирования моментов энергии элементарных частей тела:

256

Вычисление моментов инерции по приведенным формулам для тел неправильной формы является сложной задачей. Поэтому часто момент инерции тела определяют косвенными путями. Одним из них является способ физического маятника. Он заключается в том, что тело, момент инерции которого надо определить, подвешивают на горизонтальной оси в виде физического маятника и экспериментально находят период его колебаний. Далее пользуются формулой периода колебаний физического маятника, из которой выражают его момент инерции:

I = mgL4π2 T 2 .

Зная величины m, L, T по этой формуле вычисляют момент инерции

В данной лабораторной работе в качестве физического маятника используется тело, состоящее из металлического стержня, к которому с помощью винта крепится массивный металлический цилиндр. Маятник

подвешивается на горизонтальной оси, прикрепленной к стене. Для определения цен-

тра масс маятника используется призма (рис. 4.15).

Если переместить цилиндр по стержню и закрепить его в другом месте, получим тело с другим моментом инерции, другим расстоянием от оси подвеса до центра масс и, следовательно, другой период колебаний физического маятника.

Для каждого определенного положения цилиндра линейкой измеряют расстояние L от оси до центра масс; время N колебаний t измеряют секундомером (или с помощью часов) и затем находят период колебаний

T = Nt .

Масса маятника написана на цилиндре.

Задания

Iуровень

1.Укрепить цилиндр на нижнем конце стержня и определить центр масс полученного физического маятника с помощью призмы. Измерить рас-

257

стояние от центра масс до оси вращения. При данном положении цилиндра определять положение центра масс и измерять L необходимо 3 раза. Найти среднее положение Lñð .

2.Повесить маятник на горизонтальную ось (на кронштейн), отклонить его на небольшой угол (не более 10°), отпустить и одновременно начать отсчет времени. Измерить время 10 колебаний. Вычислить период колебаний (см. последнюю формулу).

3.Пункты 1 и 2 повторить для 7 различных положений цилиндра, отличающихся друг от друга на 4–5 см. Данные измерений и вычислений занести

втабл. 4.1.

4.По данным измерениям для каждого положения цилиндра (и центра масс) вычислить момент инерции маятника по приведенной выше формуле.

Построить графики:

а) I (Lñð ) — график зависимости момента инерции от расстояния (сред-

него) от оси подвеса до центра масс;

б) T (Lñð) — график зависимости периода колебаний от расстояния (среднего) от оси до центра масс.

IIуровень

1.Выполнить задания I уровня для пяти различных положений цилиндра.

2.Для одного из них найти теоретическое значение момента инерции маятника. Для этого рассмотреть маятник как систему двух тел: стержня массой m1 длиной l и цилиндра массой m2 , радиуса R , высоты h .

Известно, что момент инерции цилиндра относительно оси, совпадающей с его диаметром и проходящей через центр масс цилиндра, вычисляется по формуле:

Найденное теоретическое значение сравнить с экспериментальным.

258

7. По какому закону изменяется амплитуда A затухающих колебаний с течением времени? ( A0 — начальная амплитуда, β = const ).

Маятники

1. Формула периода колебаний пружинного маятника:

2.На нити длиной 1 м подвешен шар радиусом 1 м. Данная механическая система является физическим маятником или математическим маятником?

3.Бесконечно тонкое кольцо радиусом 1 м висит на гвозде. Это физический маятник или математический?

4.Если массу математического маятника увеличить в 2 раза, то как изменится период колебаний маятника?

5. Формула периода колебаний математического маятника длиной l :

буквой L обозначено:

а) длина физического маятника; б) расстояние от оси подвеса до центра масс маятника; в) длина оси маятника;

г) приведенная длина физического маятника.

7. Найти период колебаний маятника, представляющего собой невесомую нить длиной l , подвешенную за один конец на горизонтальную ось, если в конце нити и в ее середине находятся материальные точки одинаковой массой m .

260

Вопросы по выполнению лабораторной работы

1.Какие из перечисленных ниже величин измеряются в данной лабораторной работе?

1)момент инерции I ;

2)n — количество колебаний, до центра масс;

3)R — радиус цилиндра;

4)υ — скорость;

5)L — расстояние от точки подвеса;

6)a — ускорение;

7)t — время.

2.Какие из перечисленных ниже величин вычисляются в данной лабораторной работе?

1)υ — скорость маятника;

2)T — период колебаний;

3)a — ускорение маятника;

4)L — расстояние от точки подвеса до центра масс;

5)I — момент инерции;

8)m — масса маятника.

3.Физический маятник представляет собой тонкое кольцо радиусом R массой m , висящее на гвозде. Как изменится его момент инерции, если увеличить массу кольца?

1)момент инерции увеличится;

2)момент инерции не изменится;

3)момент инерции уменьшится.

4.Физический маятник представляет собой шар радиусом 0,5 м массой 1 кг, подвешенный на нити длиной 0,5 м. Вычислить момент инерции этого маятника относительно оси подвеса.

5.На невесомой нити подвешены две материальные точки: одна на конце нити, другая — в середине нити. Нить закреплена за свободный конец на гвозде, вбитом в стену. Какой это маятник?

1)физический;

2)математический.

4.3.2.2 Контрольные вопросы для защиты лабораторной работы

Iуровень

1.Записать выражение для смещения от положения равновесия при гармонических колебаниях и объяснить физический смысл входящих в него величин.

261

2.Дать определение физического маятника и объяснить, под действием каких сил (моментов сил) происходят его колебания. При каком условии колебания физического маятника являются гармоническими?

3.Записать формулу периода гармонических колебаний физического маятника и объяснить физический смысл входящих в нее величин.

4.Уметь получать из формулы периода колебаний физического маятника соответствующую формулу для математического маятника.

5.Объяснить порядок выполнения лабораторной работы.

IIуровень

1.Рассмотреть колебания физического маятника и получить формулу периода его колебаний.

2.Теоретически получить выражения для момента инерции и периода колебаний физического маятника данного вида, используя известное выражение момента инерции цилиндра относительно диаметральной оси, прохо-

III уровень

Дополнительно к вопросам II уровня: получить приведенное выше выражение момента инерции цилиндра.

4.4 МАТЕРИАЛЫ ДЛЯ УПРАВЛЯЕМОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ

Задание № 1

Изучить сложение взаимно перпендикулярных колебаний и биения (законспектировать).

Задание № 2

Рассмотреть теорию колебаний физического маятника, получить формулу для периода колебаний. Математический маятник (законспектировать).

Задание № 3

Решить задачи индивидуального задания по теме «Колебательное движение» из следующего ряда задач.

1 Характеристики гармонических колебаний. Энергия гармонических колебаний

262

Уровень 1

1.1. Написать уравнение гармонического колебательного движения с амплитудой 50 мм, периодом 4 с и начальной фазой ϕ = π4 . Найти смеще-

ние x колеблющейся точки от положения равновесия при t = 0 и t = 1,5 с.

[ x = sin ( π2 t +π4 ) мм, x1 = 35,2 мм; x2 = 0.]

1.2. Написать уравнение гармонического колебания точки, если его амплитуда 15 см, максимальная скорость колеблющейся точки υmax = 30 см/с,

начальная фаза ϕ = 10°. [ x = 0,15 cos ( 2t +18π ) м.]

1.3. Через какое время от начала движения точка, совершающая колеба-

тельное движение по уравнению: x = 7sin π2 t , проходит путь от положения

равновесия до максимального смещения? [t = 1 c.]

1.4. Амплитуда гармонического колебания 5 см, период 4 с. Найти максимальную скорость υmax колеблющейся точки и ее максимальное ускорение

amax . [υmax = 7,85 см/с; amax = 12,3 см/с2.]

1.5. Частица массой 0,01 кг совершает гармонические колебания с периодом 2 с. Полная энергия колеблющейся частицы — 0,1 мДж. Определить амплитуду A колебаний и наибольшее значение силы Fmax , действующей на

частицу.

[A = 0,045 м; Fmax = 4, 44 × 10-3 Н].

Уровень 2

1.6. Частица совершает колебания вдоль оси X по закону x = 6cos0,5π(t +1) . Найти путь l , пройденный частицей за период, а также

средние значения скорости υ и ускорения a за первую четверть периода. [l = 0,24 м; υ = 0,06 м/с; a = -0,094 м/с2.]

1.7.Точка совершает прямолинейные гармонические колебания. Пери-

од колебаний 2 с, амплитуда 4 см. Найти скорость точки υ в момент времени, когда смещение точки от положения равновесия x = 2 см. [υ = ±10,9 м/с.]

1.8.Через какое время от начала движения точка, совершающая гармоническое колебание, сместится от положения равновесия на половину амплитуды? Период колебаний 24 с, начальная фаза ϕ = 0. [t = 2 с.]

1.9.Амплитуда гармонических колебаний материальной точки равна 2 см, полная энергия колебаний 0,3 мкДж. При каком смещении x от положения равновесия на колеблющуюся точку действует сила 22,5 мкН?

[ x = FA2 = 1,5 см.] 2W

263

1.10. Определить отношение кинетической энергии точки, совершающей гармонические колебания, к ее потенциальной энергии, если известна

фаза колебания/ [ tg2 (ω0t +ϕ) .]

264

2 Сложение одинаково направленных гармонических колебаний одинаковой частоты. Биения. Сложение взаимно перпендикулярных колебаний одинаковой частоты

Уровень 1

2.1. Найти амплитуду A и начальную фазу ϕ гармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями x1 = 0,02sin(5πt + π2) м и x2 = 0,03sin(5πt + π4) м.

[A = 4,6 см; ϕ = 62° 46’.]

2.2. Найти амплитуду A и начальную фазу ϕ гармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями: x1 = 4sin πt см и x2 = 3sin(πt + π2) см. Написать уравнение ре-

зультирующего колебания. Дать векторную диаграмму сложения амплитуд. [А = 5 см; ϕ = 36° 52’ ≈ 0,2π , x = 5 sin(πt +π / 5) cм.]

2.3.Частоты колебаний двух одновременно звучащих камертонов настроены соответственно на 560 и 560,5 Гц. Определить период биений. [2 с.]

2.4.В результате сложения двух колебаний, период одного из которых 0,02 с, получают биения с периодом 0,2 с. Определить период второго складываемого колебания. [0,022 с.]

2.5.Точка участвует в двух взаимно перпендикулярных колебаниях

x = 2sin ωt м и y = 2cosωt м. Найти траекторию результирующего движе-

ния точки. [ х2 + у2 =1, уравнение окружности радиусом R = 2 м.]

4 4

5.6. Складываются два гармонических колебания одного направления с частотами 460 Гц и 461 Гц. Найти период τ биений. [τ =1,0 c.]

5.7. Написать уравнение движения x(t) частицы, одновременно участ-

Уровень 2

2.8. Результирующее колебание точки, участвующей в двух колебаниях одного направления, описывается выражением: x = Acos2,1t cos80t . Найти

период биений τ и циклические частоты ω1 и ω2 складываемых колебаний.

265

2.9. Точка одновременно участвует в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями: x = sin πt мм и y = 2cos π(t +0,5) мм.

3 Пружинный, математический и физический маятники

Уровень 1

3.1.Один математический маятник длиной 2 м совершает за некоторое время в 2 раза больше колебаний, чем другой математический маятник за то же время. Определить длину второго математического маятника. [8 м.]

3.2.При увеличении длины математического маятника на 5 м период колебаний увеличивается в 1,5 раза. Определить начальную длину математического маятника. [4 м.]

3.3.Висящее на пружине тело массой m совершает гармонические колебания. Во сколько раз возрастает период колебаний, если к этому телу под-

весить еще одно тело массой 8m ? [В 3 раза.]

3.4. При подвешивании грузов массами m1= 600 г и m2 = 400 г к сво-

бодным пружинам последние удлинились одинаково ( l = 10 см). Пренебрегая массой пружин, определить: 1) периоды колебаний грузов; 2) какой из грузов при одинаковых амплитудах обладает большей энергией и во сколько раз.

[1) T1 = T2 = 0,63 с; 2) груз большей массой, в 1,5 раза.]

3.5. Обруч радиусом 19,6 см, подвешенный на гвозде, вбитом в стенку, совершает малые колебания в плоскости, параллельной стене. Найти период колебаний данного маятника [1,256 с].

5.6. Однородный шарик радиусом 10 см подвешен на нити длиной 0,215 м. Этот физический маятник можно рассматривать как математический, но при таком допущении относительная ошибка в определении периода колеба-

ний равна δT = T2 −T1 где T1 — период колебаний математического маятни-

T1

ка; T2 — период колебаний физического маятника. Определить δT . [23,5%.]

Уровень 2

3.7. Математический маятник, состоящий из нити длиной 1 м и свинцового шарика радиусом 2 см, совершает гармонические колебания с амплиту-

266

дой 6 см. Определить: 1) скорость шарика при прохождении им положения равновесия; 2) максимальное значение возвращающей силы. Плотность свинца ρ = 11,3 г/см3; [1) 0,186 м/с; 2) 69,5 м Н.]

3.8. На чашку весов массой M , подвешенную на пружине с жесткостью k , с высоты h падает небольшой груз массой m . Удар груза о дно чашки является абсолютно неупругим. Чашка в результате падения груза начинает совершать колебания. Определить амплитуду A этих колебаний.

3.9. Тонкий однородный стержень длиной 60 см может свободно вращаться вокруг горизонтальной оси, проходящей через верхний конец стерж-

ня. Стержень отклонили на угол 0,01 рад и в момент времени t = 0 отпустили. Считая колебания малыми, определить период колебаний стержня и записать функцию α(t) . [1,27 с, α(t) = 0,01 cos 1,57 πt рад.]

3.10. Маятник состоит из стержня длиной 30 см, массой 50 г, на верхнем конце которого укреплена материальная точка массой 40 г, на нижнем — шарик радиусом 5 см, массой 100 г). Определить период колебаний этого маятника около горизонтальной оси, проходящей через точку 0 в центре стерж-

ня. [1,24 с.]

4 Затухающие колебания. Вынужденные колебания

Уровень 1

4.1.Логарифмический декремент затухания математического маятника 0,2. Во сколько раз уменьшится амплитуда колебаний за одно полное колебание маятника? [1,22.]

4.2.Амплитуда затухающих колебаний математического маятника за 1 мин уменьшилась вдвое. Во сколько раз уменьшится амплитуда за время

3 мин? [8.]

4.3.Тело массой 360 г подвешено на пружине с коэффициентом жесткости 16 Н/м и совершает вертикальные колебания в некоторой среде. Логарифмический декремент затухания 0,01. Сколько колебаний должно совершить тело, чтобы амплитуда смещения уменьшилась в e раз? За какой промежуток времени произойдет это уменьшение амплитуды? [N = 100; τ = 94 с.]

4.4.Груз массой 0,1 кг подвесили на пружину, которая при этом растянулась на 0,15 см. Если систему вывести из положения равновесия и отпус-

темы. Если на эту систему действует периодическая вынуждающая сила, амплитудное значение которой F0 = 1,8 Н, на определенной частоте наблюда-

ется возрастание амплитуды колебаний до резонансного значения. Найти резонансное значение амплитуды Aðåç . [39,8 см.]

267

4.5. На пружине, коэффициент жесткости которой 820 Н/м висит железный шарик массой 0,2 кг. Со стороны переменного магнитного поля на шарик действует синусоидальная сила, амплитудное значение которой 3Н и

циклическая частота Ω = bω0 , где b =0,8, ω0 — собственная частота колебаний пружинного маятника. Коэффициент сопротивления среды r = 0,025

HMc . Найти амплитуду вынужденных колебаний. [1,02 см.]

Уровень 2.

4.6. Найти коэффициент затухания β и логарифмический декремент затухания d математического маятника, если известно, что за 100 с колебаний полная механическая энергия маятника уменьшилась в десять раз. Длина ма-

ятника 0,98 м. [β = 0,0115 с-1; d= 0,023.]

4.7. Частица совершает прямолинейные затухающие колебания с периодом 4,5 с. Начальная амплитуда колебаний 0,16 м, а амплитуда после 20 полных колебаний 0,01 м. Определить коэффициент затухания β и логарифмический декремент затухания d . Написать уравнение колебаний частицы, приняв начальную фазу колебаний равной 0. [β = 0,031с-1, λ = 0,14.]

4.8. Тело массой 12 г совершает затухающие колебания с циклической частотой 3,14 с-1. При этом за время 60 с тело теряет 0,9 своей полной механической энергии. Найти коэффициент затухания β; коэффициент сопротив-

ления среды r ; добротность колебательной системы Q .

[β = 0,019 с-1; r = 0,46 мНМ с ; Q = 83.]

4.9. Математический маятник совершает затухающие колебания в среде, логарифмический декремент затухания d1 = 1,26. Определить логариф-

мический декремент затухания d2 маятника, если сопротивление среды возрастает в 2 раза. Во сколько раз nmin надо увеличить сопротивление среды, чтобы движение маятника стало апериодическим? [d2= 2,69; nmin = 5,1 раза.]

4.10. Тело массой m = 10 г совершает затухающие колебания с максимальной амплитудой Amax = 7 см, начальной фазой ϕ = 0 и коэффициентом

затухания β = 1,6 с-1. На это тело начала действовать внешняя периодическая сила, под действием которой установились вынужденные колебания. Урав-

нение вынужденных колебаний имеет вид x = 5sin(10πt − 43 π) см. Найти

(с числовыми коэффициентами) уравнение свободных затухающих колебаний и уравнение вынуждающей силы. [ x = 7e−1,6t sin10,5πt см,

F = 72sin πt мН.]

268

4.3.1Лабораторная работа «Изучение кинематических величин

исвязи между ними при поступательном и вращательном движениях

271

МОДУЛЬ 3 ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА . . . . . 142

1 Введение. Базовые проблемы модуля . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143 2 Учебно-информационная модель модуля. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143 324B Научно-теоретический материал . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144 325B .1 Словарь понятий . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144 3.1.1 Новые понятия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144 3.1.2 Понятия для повторения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 145

3.2 Основной теоретический материал . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 146 3.2.1 Динамика вращательного движения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 146 3.2.1.1 Момент силы. Момент пары сил. . . . . . . . . . . . . . . . . . . . . . . . . 146 3.2.1.2 Момент импульса материальной точки. . . . . . . . . . . . . . . . . . . . 150

3.2.1.3Закон сохранения момента импульса механической системы . 151

3.2.1.4Момент импульса тела, вращающегося

вокруг неподвижной оси. Момент инерции тела . . . . . . . . . . . 154

272

3.2.1.5 Основной закон динамики вращательного движения твердого тела вокруг неподвижной оси . . . . . . . . . . . . . . . . . . . 159

3.2.1.6 Кинетическая энергия вращательного движения . . . . . . . . . . . 160 3.3 Дополнительный материал . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 164 3.3.1 Движение в неинерциальных системах отсчета. . . . . . . . . . . . . . . . . . . . . 164

3.3.1.1 Силы инерции при поступательном движении неинерциальной системы отсчета . . . . . . . . . . . . . . . . . . . . . . . 164

3.3.1.2 Центробежная сила. Сила Кориолиса . . . . . . . . . . . . . . . . . . . . . 169 426B Материалы, используемые в процессе обучения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171 427B .1 Материалы к лекциям . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171 4.2 Материалы к практическому занятию «Динамика вращения твердого тела» . . . . 175 4.2.1 Момент инерции. Момент силы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 175 4.2.2 Закон динамики вращательного движения твердого тела . . . . . . . . . . . . 177 4.2.3 Момент импульса. Закон сохранения момента импульса . . . . . . . . . . . . . 180

4.2.4 Кинетическая энергия вращательного движения. Работа внешних сил при вращении твердого тела вокруг неподвижной оси . . . . . . . . . . . . . . 182

4.3 Материалы к лабораторным занятиям . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 184 4.3.1 Лабораторная работа «Определение момента инерции твердого тела» . 184 4.3.2 Контрольные задания к лабораторной работе . . . . . . . . . . . . . . . . . . . . . . 191

4.3.2.1 Вопросы предварительного контроля (компьютерный допуск к лабораторной работе) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 191

4.3.2.2 Контрольные вопросы для защиты лабораторной работы . . . . 194 4.4 Материалы для управляемой самостоятельной работы студентов . . . . . . . . . . . . . 194

МОДУЛЬ 4 КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 203 1 Введение. Базовые проблемы модуля. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 203 2 Учебно-информационная модель модуля . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 204 3 Научно-теоретический материал . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 205 3.1 Словарь понятий . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 205 3.1.1 Новые понятия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 205 3.1.2 Понятия для повторения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206

3.2 Основной теоретический материал . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206 3.2.1 Колебательное движение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206

3.2.1.1 Дифференциальное уравнение гармонических колебаний.

Пружинный маятник . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206 3.2.1.2 Энергия гармонических колебаний . . . . . . . . . . . . . . . . . . . . . . . 212 3.2.1.3 Сложение одинаково направленных гармонических

колебаний одинаковой частоты . . . . . . . . . . . . . . . . . . . . . . . . . 213 3.2.1.4 Биения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 216 3.2.1.5 Сложение взаимно перпендикулярных колебаний

одинаковой частоты . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 217 3.2.1.6 Затухающие колебания. Дифференциальное уравнение

затухающих колебаний и его решение . . . . . . . . . . . . . . . . . . . 220 3.2.1.7 Характеристики затухающих колебаний . . . . . . . . . . . . . . . . . . 224 3.2.1.8 Вынужденные колебания . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 228 3.2.1.9 Механический резонанс . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 232

3B82 .3 Дополнительный материал . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 235 3.3.1 Физический и математический маятники . . . . . . . . . . . . . . . . . . . . . . . . . . 235 4 Материалы, используемые в процессе обучения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 239

4.1 Материалы к лекциям . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 239 4.2 Материалы к практическому занятию «Колебательное движение» . . . . . . . . . . . . 243

4.2.1 Характеристики гармонических колебаний.

Энергия гармонических колебаний . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 243

4.2.2Сложение одинаково направленных гармонических колебаний одинаковой частоты. Биения. Сложение взаимно перпендикулярных

колебаний одинаковой частоты . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 245 4.2.3 Пружинный, математический и физический маятники . . . . . . . . . . . . . . . 248

273

4.2.4 Затухающие колебания. Вынужденные колебания . . . . . . . . . . . . . . . . . . 251 4.3 Материалы к лабораторным занятиям . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 253

4.3.1 Лабораторная работа «Определение момента инерции физического маятника» . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 253

4.3.2 Контрольные задания к лабораторной работе . . . . . . . . . . . . . . . . . . . . . . 258 4.3.2.1 Вопросы предварительного контроля (компьютерный допуск

к лабораторной работе) 258 4.3.2.2 Контрольные вопросы для защиты лабораторной работы . . . . 260 4.4 Материалы для управляемой самостоятельной работы студентов . . . . . . . . . . . . . 261

5 Образец контрольных заданий для проверки результатов обучения . . . . . . . . . . . . . . . . . . . . 167

ЛИТЕРАТУРА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 268

274