
Механика материалов в примерах и задачах
.pdfМИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА И ПРОДОВОЛЬСТВИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования «БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра сопротивления материалов и деталей машин
МЕХАНИКА МАТЕРИАЛОВ В ПРИМЕРАХ И ЗАДАЧАХ
Учебно-методическое пособие
Минск
БГАТУ
2009
УДК 539.3/.6(07) ББК 30.121я7
М 55
Рекомендовано научно-методическим советом факультета «Технический сервис в АПК» БГАТУ
Протокол № 3 от 19 марта 2009 г.
Составители:
канд. техн. наук, доц. О.И. Мисуно (разделы 1 – 4, 6, 7), канд. техн. наук, доц. Д.Н. Колоско (разделы 1, 5), ст. преподаватель С.А. Легенький (разделы 6, 7)
Рецензенты: д-р техн. наук, проф., зав. каф. теоретической механики и ТММ БГАТУ А.Н. Орда;
канд. техн. наук, доц., зав. каф. деталей машин и ПТУ БГТУ
С.Е. Бельский
Механика материалов в примерах и задачах: учебно-
М55 методическое пособие / сост. О.И. Мисуно, Д.Н. Колоско, С.А. Легенький. – Минск : БГАТУ, 2009. – 72 с.
ISBN 978-985-519-162-0.
Учебно-методическое пособие содержит задания и образцы их выполнения по дисциплине «Механика материалов» для самостоятельной работы и контроля учебной деятельности студентов очной и заочной форм обучения агроинженерных специальностей.
УДК 539.3/.6(07) ББК 30.121я7
ISBN 978-985-519-162-0 |
© БГАТУ, 2009 |
2
ВВЕДЕНИЕ
Механика материалов − наука о прочности, жесткости и устойчивости отдельных элементов конструкций (сооружений и машин).
Инженеру любой специальности часто приходится производить расчеты на прочность, жесткость и устойчивость. Неправильный расчет самой незначительной, на первый взгляд, детали может повлечь за собой очень тяжелые последствия − привести к разрушению конструкции в целом. При проведении подобных расчетов на прочность необходимо стремиться к сочетанию надежности работы конструкции с ее экономичностью, добиваться наибольшей прочности при наименьшем расходе материала. Необходимо повышать эффективность проектных решений, применять новые прогрессивные конструкционные материалы.
Механика материалов − одна из сложных дисциплин, изучаемых в высших технических учебных заведениях; занятия по этому курсу должны обязательно сопровождаться составлением конспекта и решением задач. Если при решении задач возникают затруднения, следует воспользоваться имеющимися в задачниках указаниями и решениями, но совершенно необходимо научиться самостоятельно решать задачи и делать выводы формул. При этом необходимо обращать особое внимание на физическую сущность явления и на те допущения и ограничения, которые делаются в процессе выводов. Д. И. Менделеев в предисловии к первому изданию «Основ химии» писал: «Знание выводов без сведений о способах их достижения может легко привести к заблуждению не только в философской, но и практической стороне наук, потому что тогда неизбежно необходимо придавать абсолютное значение тому, что нередко относительно и временно». Поэтому необходимо полностью понимать чертежи и схемы, которыми сопровождаются выводы формул. Выдающийся русский ученый, отец русской авиации Н. Е. Жуковский писал: «Раз усвоенные геометрические образы, рисующие картину рассматриваемого явления, надолго западают в голову и живут в воображении изучающего».
После изучения каждой темы надо обязательно ответить на вопросы для самопроверки; это способствует лучшему усвоению пройденного материала.
3
ОБЩИЕ УКАЗАНИЯ ПО РЕШЕНИЮ ЗАДАЧ
1. Студент обязан взять из таблицы, прилагаемой к условию задачи, данные в соответствии со своим личным номером (шифром) и первыми шестью буквами русского алфавита, которые следует расположить под шифром, например:
шифр − 0 1 2 3 4 5 6;
буквы − а б в г д е .
В том случае, когда личный номер состоит из семи цифр, первая цифра шифра не учитывается.
Из каждого вертикального столбца любой таблицы, обозначенного внизу определенной буквой, надо взять только одно число, стоящее в той горизонтальной строке, номер которой совпадает с номером буквы. Например, вертикальные столбцы таблицы 1.1 обозначены буквами е, г и д. В этом случае при указанном выше личном номере (шифре) 0 1 2 3 4 5 6 студент должен взять из столбцов: е – строку номер 6 (схема на рисунке 1.2 − VI, высота полосы h = 180 мм, швеллер № 18а), из столбца г − строку номер 4 (ширина полосы b = 24 мм) и из столбца д − строку номер 5 (равнобокий уголок 140×90×8).
Задачи, выполненные с нарушением этих указаний, не засчитываются.
2.Не следует приступать к решению задач, не изучив соответствующего раздела курса. Если основные положения теории усвоены слабо и студент обратил мало внимания на подробно разобранные в курсе примеры, топрирешениизадачвозникнутбольшиезатруднения.
3.Перед решением каждой задачи надо выписать полностью ее условие с числовыми данными, составить расчетную схему и указать на ней в числах все величины, необходимые для расчета.
4.Решение должно сопровождаться краткими, последовательными и грамотными (без сокращения слов) объяснениями и чертежами, на которых все входящие в расчет величины должны быть показаны в числах. Надо избегать многословных пояснений и пересказа учебника. При пользовании формулами или данными, отсутствующими в пособии, необходимо кратко и точно указывать их источник (автор, название, издание, страницу, номер формулы).
5.Необходимо указывать единицы всех величин и подчеркивать окончательные результаты.
6.Не следует вычислять большое число значащих цифр, вычисления должны соответствовать необходимой точности.
4
1. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
Теоретические вопросы, изучение которых необходимо для успешного решения задач
Литература: [1, С. 166–197], [2, С. 121–132], [3, задачи 5.1, 5.2, 5.3, 5.5, 5.8, 5.9, 5.10, 5.15, 5.16, 5.21].
Статические моменты сечений, их изменение при параллельном переносе осей. Центр тяжести сечения. Осевой, центробежный, полярный моменты инерции сечения, их свойства, изменение при параллельном переносе и при повороте осей. Главные центральные оси инерции и главные моменты инерции. Определение моментов инерции сечений простой формы (прямоугольник, круг, кольцо). Моменты инерции сечений стандартных прокатных профилей. Свойства симметричных сечений. Определение главных центральных осей инерции и главных моментов инерции сложного сечения. Радиусы инерции.
Задача 1
Для заданного поперечного сечения бруса, состоящего из полосы (сечение прямоугольник: h − больший размер, b − меньший размер), стандартных прокатных профилей швеллера и неравнополочного уголка (рисунок 1.1) провести главные центральные оси инерции и определить величину главных центральных моментов инерции. Данные принять из таблицы 1.1.
Методические указания для решения задачи 1
1.Вычертить в масштабе 1 : 1 или 1 : 2 заданное поперечное сечение бруса.
2.Разбить заданное сложное сечение на простейшие элементы (швеллер, неравнополочный уголок, полоса) и присвоить им порядковые номера (1, 2, 3 и т.д.).
3.Последовательно для каждого элемента:
−вычертить его отдельно в заданном положении и указать все размеры;
−провести центральные оси инерции параллельно основным контурам, обозначить их zсi, yci, где i − порядковый номер элемента
5
вэтом и других обозначениях;
−провестиглавныецентральныеосиинерции, обозначитьих(υi, ui);
−установить геометрические характеристики: положение центра
тяжести, площадь сечения Аi, осевые J zi , J yi и центробежный
J zi yi моменты инерции относительно собственных центральных осей инерции, главные центральные моменты инерции Jυi , Jui .
4. На чертеже заданного поперечного сечения бруса:
−провести вспомогательные координатные оси zо, yо так, чтобы они были параллельны центральным осям как можно большего количества элементов и совпадали с основным контуром, при этом, желательно, чтобы заданное сечение оказалось в первом квадранте;
−провести центральные оси инерции zсi, yci каждого элемента;
−определить координаты центров тяжести элементов, показать
их на чертеже как расстояния zi, yi между центральными осями инерции zсi, yci и вспомогательными координатными осями zо, yо.
5. Относительно вспомогательных осей определить координаты
центра тяжести заданного сечения zс, yc , показать их на чертеже и провести через центр тяжести центральные оси инерции zс, yс параллельно осям zо, yо.
6. Определить и показать на чертеже расстояния между центральными осями каждого элемента и центральными осями заданного сечения (zсi и zс, yci и yс), обозначив их, соответственно, аi и bi.
7. Для заданного сечения определить осевые J zc , J yc и центро-
бежный J |
моменты инерции относительно центральных осей |
инерции. |
zc yc |
|
8.Определить положение главных центральных осей инерции заданного сечения, провести и обозначить их на чертеже буквами υ
иu (υ − ось, относительно которой момент инерции принимает
максимальное значение, u − ось, относительно которой момент инерции принимает минимальное значение), указать угол αглавн.
9.Вычислить величины главных центральных моментов инерции заданного сечения Jυ, Ju .
10.Проверить правильность вычисления по свойству инвариантности суммы осевых моментов инерции при повороте осей, а также по условию равенства нулю центробежного момента инерции заданного сечения относительно главных центральных осей Jυ u .
6
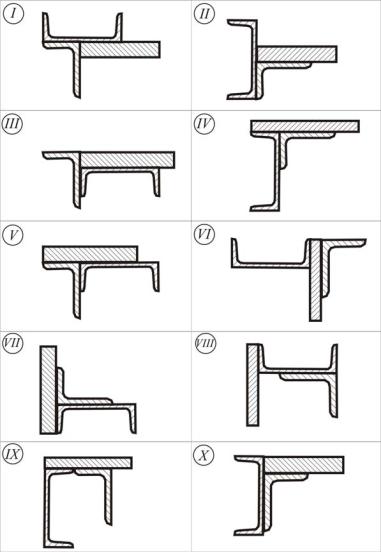
Таблица 1.1 – Исходные данные к задаче 1
строки№ |
Схемапо рисунку1.2 |
|
|
Элементы заданного сечения |
||
Полоса |
|
Швеллер |
Неравнополочный |
|||
|
|
|
||||
|
|
|
|
|
||
|
|
h, мм |
|
b, мм |
ГОСТ8240-72 |
уголок ГОСТ 8510-86 |
|
|
|
|
|
|
|
1 |
I |
155 |
|
38 |
14 |
140×90×10 |
2 |
II |
160 |
|
28 |
14а |
110×70×8 |
3 |
III |
165 |
|
34 |
16 |
125×80×7 |
4 |
IV |
170 |
|
24 |
16а |
125×80×12 |
5 |
V |
175 |
|
36 |
18 |
140×90×8 |
6 |
VI |
180 |
|
26 |
18а |
80×50×6 |
7 |
VII |
185 |
|
32 |
20 |
90×56×8 |
8 |
VIII |
190 |
|
20 |
20а |
100×63×7 |
9 |
IX |
195 |
|
26 |
22 |
100×63×10 |
0 |
X |
200 |
|
30 |
22а |
125×80×10 |
|
е |
е |
|
г |
е |
д |
Пример решения задачи 1
Схема для примера выбрана произвольно, числовые данные взя-
ты для шифра с последними цифрами 8, 2, 4: г |
д |
е |
8 |
2 |
4. |
Из столбца, в котором последняя строка обозначена буквой г, следует брать данные по восьмой строке; буквой д – по второй строке; буквой е – по четвертой. Данные будут следующими: h = 170 мм; b = 20 мм; швеллер № 16а, неравнополочный уголок
110×70×8.
Решение.
1. Вычерчиваем заданное поперечное сечение в выбранном масштабе (рисунок 1.2).
2. Разбиваем сложное сечение на простейшие фигуры и присваиваем им порядковые номера: полоса – 1, швеллер – 2, неравнополочный уголок – 3.
Рисунок 1.1 – Схема поперечного сечения бруса
7 |
8 |
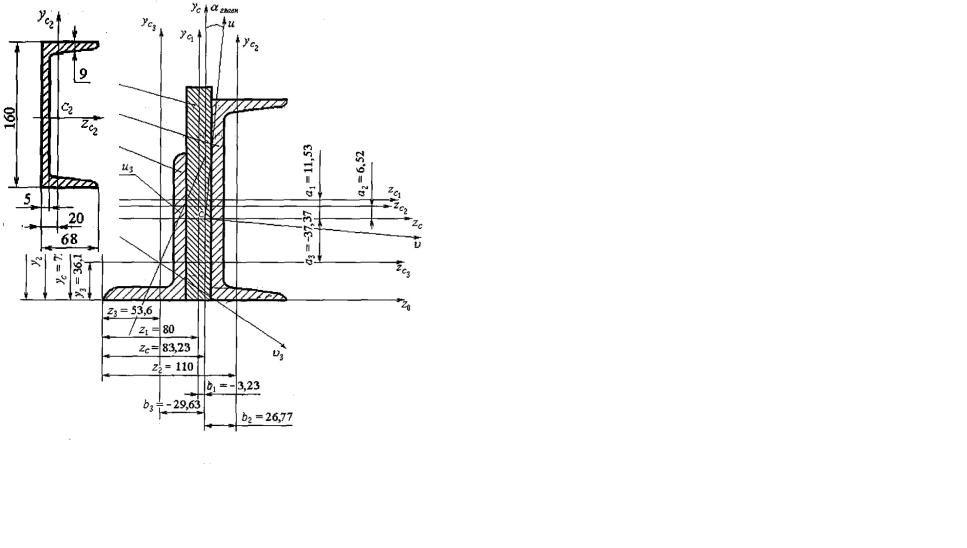
3. Каждый элемент вычерчиваем отдельно в заданном положении с указанием размеров и положения центра тяжести (рисунки 1.3…1.5). Рассчитываем или выписываем из таблиц сортамента геометрические характеристики: площадь сечения А, осевые Jz и Jy центробежный Jzy моменты инерции относительно центральных осей инерции, главные центральные моменты инерции Jυ иJu.
1. Полоса 20×170
|
|
|
А = b h = 20 170 = 3 400 мм2 ; |
|||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J z |
= |
|
b h3 |
|
= |
|
20 1703 |
|
= 8 188 333 мм = 81,88·105 мм4; |
||||
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
12 |
|
|
|
|
|
12 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J y |
= |
h b3 |
= |
170 203 |
|
=113 333 мм4 = |
|||||||
|
|
|
|
|
|
|||||||||||
|
|
|
1 |
12 |
|
|
|
|
|
12 |
|
|
|
|
||
|
|
|
=1,133 105 |
мм4. |
|
|
|
|
||||||||
Рисунок 1.3 – Полоса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2. |
Швеллер № 16а |
|
|
|
|
|
|
|
|
||||||
A =19,5 см2 |
=1950 мм2 |
; |
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
= 823 см4 |
= 82, 3 105 |
мм4 ; |
|
|
|
|
|||||||||
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
= 78,8 см4 = 7,88 105 |
мм4 . |
|
|
|
|
||||||||||
|
у2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для полосы и швеллера центральные |
|||||||||||||||
оси совпадают с главными центральными |
||||||||||||||||
в силу симметричности этих |
фигур, |
по- |
||||||||||||||
этому |
оставлено обозначение |
zс , |
ус |
и |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
zс2 , ус2 . Центробежные моменты инерции
таких фигур относительно главных центральных осей равны 0.
Рисунок 1.2 – Заданное поперечное сечение бруса
Рисунок 1.4 – Швеллер
9 |
10 |

3. Уголок неравнополочный
110х70х8
A3 = 13,9 см2 = 1390 мм2;
Jz3 =172 см4 =17, 2 105 мм4 ;
J у3 = 54,6 см4 = 5, 46 105 мм4 ;
Ju3 =32,3 см4 = 3, 23 105 мм4 ; tg α = 0,4 α = 21°48΄;
y0 = 36,1мм; z0 = 16,4 мм.
Рисунок 1.5 ― Уголок неравнополочный
Максимальный осевой момент инерции уголка Jυ3 определяем
из свойства инвариантности суммы осевых моментов инерции при повороте осей:
J z + J у = Jυ + Ju .
Откуда
Jυ3 = Jz3 + J у3 − Ju3 =172 +54, 6 −32,3 =194,3 см4 =19, 4 105 мм4 .
Центробежный момент инерции определяем по формуле:
J |
z3 у3 |
= |
Jυ3 |
− Ju3 |
sin 2α3 |
= |
194,3 −32,3 |
0, 689 =55,809 см4 = |
||
|
2 |
|
2 |
|
||||||
|
|
|
|
|
|
|
||||
=5,581 10−5 мм4. |
|
|
|
|
|
|||||
Угол α принимаем положительным, |
т.к. поворот осей υ и u до |
|||||||||
совмещения с осями z3 и у3 производится против хода часовой стрелки.
4. Проводим вспомогательные координатные оси z0 и у0 таким образом, чтобы они совпадали с основным контуром, сечение располагалось в первом квадранте. Проводим центральные оси каждого элемента, обозначаем координаты центров тяжести элементов относительно этих вспомогательных осей:
11
z1 = 70 + |
20 |
|
=80мм; |
|
z2 = 70 +20 +20 =110 мм; z3 = 53,6 мм; |
||||||||||||
|
170 |
|
|
2 |
|
|
|
|
|
|
|
160 |
|
|
|
|
|
у1 = |
=85 мм; |
у2 = |
=80 мм; |
у3 = 36,1 мм. |
|||||||||||||
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
5. Определяем координаты центра тяжести всего сечения: |
|||||||||||||||||
|
|
|
z |
|
= |
∑Sу |
= |
|
z1 А1 + z2 А2 + z3 |
А3 |
= |
||||||
|
|
|
с |
|
∑А |
|
|
|
А1 + А2 + А3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
= 80 3 400 +110 1950 +53,6 1390 =83, 23 мм; |
||||||||||||||
|
|
|
|
|
|
|
|
3 400 +1950 +1390 |
|
|
|
||||||
|
|
|
y |
|
= |
∑Sz |
= |
|
у1 А1 + у2 А2 + у3 А3 |
= |
|||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
с |
|
|
∑А |
|
|
|
|
А1 + А2 + А3 |
|
|
|
||
= 85 3 400 +80 1950 +36,1 1390 =73, 47 мм. 3 400 +1950 +1390
Откладываем их на чертеже, обозначаем центр тяжести с и проводим через него центральные оси инерции zc и ус параллельно вспомогательным осям z0 и у0.
6. Рассчитываем расстояния между центральными осями каждого элемента и центральными осями всего сечения:
а1 = у1 − ус =85 −73,47 =11,53 мм, b1 = z1 − zс = 80 −83,23 = −3,23 мм, а2 = у2 − ус = 80 −73,47 = 6,52 мм,
b2 = z2 − zс =110 −83,23 = 26,77 мм,
а3 = у3 − ус = 36,1 − 73,47 = −37,37 мм,
b3 = z3 − zс = 53,6 − 83,23 = −29,63 мм.
Обозначаем их на чертеже.
7. Определяем осевые и центробежный моменты инерции сечения относительно центральных осей инерции, используя формулы изменения этих моментов при параллельном переносе осей:
12
J |
zс |
= J |
z1 |
+ a 2 |
A |
+ J |
z2 |
+ а2 |
А |
2 |
+ J |
z |
+ а |
2 |
А = 81,88 10 5 +11,532 |
3 400 + |
||||
|
|
1 |
1 |
|
|
2 |
|
|
|
|
3 |
3 |
3 |
|
||||||
+82, 3 1 0 5 + 6, 5 2 2 1 950 + 1 7, 2 10 5 + (−3 7, 37 )2 1 3 90 = |
|
|||||||||||||||||||
= 206,1 43 10 5 |
мм4 ; |
|
|
|
|
|
|
|
|
|
|
|||||||||
J |
у |
|
= J |
у |
+b2 |
A + J |
у |
|
+b2 |
А + J |
у |
|
+b2 |
А =1,133 105 +(−3,23)2 3 400 + |
||||||
|
с |
|
1 |
1 |
|
2 |
2 |
|
2 |
|
|
3 |
3 |
|
3 |
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
+7,88 105 +26,772 1 950 +5,46 105 +(−29,63)2 1390 = 41,005 105 мм4 ;
Jz у |
= Jz у |
+a1 b1 А1 + Jz у |
+a2 b2 А2 + Jz у +a3 b3 А3 = |
|
с с |
1 1 |
2 |
2 |
3 3 |
=0 +11,53 (−3, 23)×3400 |
+0 +6,52 26,77 1950 +5,581 105 + |
|||
+(−37,37) |
(−29,63) 1390 |
= 20,828 мм4. |
||
8. Определяем положение главных центральных осей инерции заданного сечения по формуле:
tg2αглавн. = − |
2 Jzс ус |
|
− |
2 |
20,828 105 |
|
= |
|
|
Jz − J |
у |
|
|
5 |
5 |
|
|||
|
с |
206,143 10 −41, 005 10 |
|
||||||
|
с |
|
|
|
|
|
|
||
= − 0, 252 2αглавн |
|
|
|
|
D ′ |
αглавн = −7 |
D ′ |
||
= arctg(-0,252) = −14 9 |
4 . |
||||||||
Знак «−» означает, что центральные оси zc и ус нужно повернуть по часовой стрелке, чтобы они совпали с главными центральными
осями υ и u. Обозначаем угол αглавн и оси υ и u на чертеже.
9. Рассчитываем величины главных центральных моментов инерции сечения, используя формулы изменения моментов инерции при повороте осей:
Jυ = J zс cos2 α + J ус sin2 α − J zс ус sin 2α,
где α = αглавн cos α = 0,9923, cos2α = 0,9848, cos2α = 0,9696, sinα = –0,1232, sin2α = 0,0152, sin2α = –0,2445;
Jυ = 206,143·105·0,9848 + 41,005·105·0,0152 – 20,828·105(–0,2445) = 208,725·105 мм4;
Ju = Jzc ·sin2α + Jyc cos2α +Jzcyc sin2α = 206,143 · 105 · 0,015 + 41,005 · · 105 × 0,9848 + 20,828 · 105(–0,2445) = 38,423 · 105 мм4.
13
10. Проверяем правильность вычисления главных моментов инерции сечения по свойству инвариантности суммы осевых моментов инерции при повороте осей:
J zс + J ус = Jυ + Ju ,
206,143 105 + 41,005 105 = 208,725 105 +38,423 105 ,
247 ,148 10 5 = 247 ,148 10 5 ;
по условию равенства нулю центробежного момента инерции сечения относительно главных центральных осей:
Jυu = |
Jzс − J ус |
sin 2α+ Jz у |
cos 2α = |
||
2 |
|||||
|
с |
с |
|
||
|
|
|
|||
= 206,143 105 −41, 005 105 |
(−0, 2445)+ |
||||
|
|
2 |
|
|
|
+20,828 105 0,9696 =−20,188 105 +20,194 105 =0,006 105 мм4.
Определяем погрешность вычислений:
0, 006 105 |
100 = 0, 029 % <3 %. |
|
20,188 105 |
||
|
Следовательно, задача решена верно.
2. ТЕОРИЯ НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ. ТЕОРИИ ПРОЧНОСТИ
Теоретические вопросы, изучение которых необходимо для успешного решения задач
Литература: [1, С. 74–119], [2, С. 252–270, 275–284, 292−310], [3, 7 задачи2.8, 2.11, 2.12, 2.18, 2.19, 2.28, 2.29, 2.30, 2.31].
Напряженное состояние в точке. Компоненты напряжения и их обозначения. Закон парности касательных напряжений. Нормальные и касательные напряжения на произвольной площадке, проходящей через данную точку. Главные площадки и главные напряжения. Экстремальные касательные напряжения. Чистый сдвиг. Главные напряжения при чистом сдвиге. Обзор различных видов напряженных состояний.
Деформированное состояние в точке. Основные понятия, компоненты деформированного состояния. Главные оси деформированного состояния и главные деформации. Объемная деформация.
14
Закон Гука при растяжении и сжатии. Модуль упругости (модуль Юнга), коэффициент Пуассона, их физический смысл. Закон Гука при сдвиге. Модуль сдвига. Связь между упругими постоянными для изотропного тела. Обобщенный закон Гука. Удельная потенциальная энергия деформации, ее составляющие в общем случае напряженного состояния.
Назначение и сущность теорий прочности. Эквивалентное напряженное состояние и эквивалентное напряжение. Классические теории прочности: теория наибольших нормальных напряжений, теория наибольших относительных удлинений, теория наибольших касательных напряжений, энергетическая теория прочности. Применение классических теорий прочности. Теория прочности Мора и ее практическое применение.
Задача 2
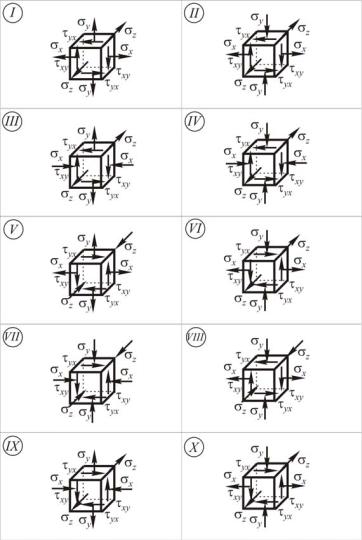
В окрестности опасной точки стальной конструкции выделен бесконечно малый элемент в виде прямоугольного параллелепипеда. На его гранях действуют нормальные (σх, σу, σz) и касательные (τху, τух) напряжения (рисунок 2.1). Требуется: определить и показать главные площадки и главные напряжения; определить максимальные касательные напряжения; найти главные деформации и относительное изменение объема; определить удельную потенциальную энергию деформации; проверить прочность материала, используя третью и четвертую классические теории прочности, принимая [σ] = 160 МПа. Данные к задаче принять из таблицы 2.1.
Методические указания для решения задачи 2
1.Определить по формуле величину угла, на который следует повернуть грани исходного элемента до их совмещения с главными площадками.
2.Показать на схеме угол, найденный в п. 1, и главные площадки.
15
Рисунок 2.1 – Схемы нормальных и касательных напряжений, действующих по граням выделенного элемента
16

|
Таблица 2.1 – |
Исходные данные к задаче 2 |
|
|||||
|
|
|
|
|
|
|
|
|
№строки |
Схемапо рисунку2.1 |
|
Напряжения (приведены по модулю) |
|
||||
σх, МПа |
|
|
σу, МПа |
σz, МПа |
|
τху, МПа |
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
I |
20 |
|
|
75 |
10 |
|
18 |
2 |
II |
25 |
|
70 |
15 |
|
20 |
|
3 |
III |
30 |
|
65 |
20 |
|
22 |
|
4 |
IV |
35 |
|
60 |
25 |
|
24 |
|
5 |
V |
40 |
|
55 |
30 |
|
26 |
|
6 |
VI |
45 |
|
50 |
25 |
|
28 |
|
7 |
VII |
50 |
|
45 |
20 |
|
25 |
|
8 |
VIII |
55 |
|
40 |
15 |
|
23 |
|
9 |
IX |
60 |
|
35 |
10 |
|
21 |
|
0 |
X |
65 |
|
30 |
25 |
|
17 |
|
|
е |
д |
|
|
е |
г |
|
е |
|
|
|
|
|
|
|
|
|
3.Найти на параллельных оси z площадках экстремальные нормальные напряжения и обозначить главные напряжения.
4.Показать на схеме главные напряжения.
5.Зная величины наибольшего и наименьшего из главных напряжений, определить максимальные касательные напряжения.
6.Используя обобщенный закон Гука, определить главные деформации и относительное изменение объема.
7.Используя главные напряжения, определить удельную потенциальную энергию деформации.
8.Записать условие прочности согласно третьей классической теории прочности (теории наибольших касательных напряжений) и, подставив наибольшее и наименьшее из главных напряжений, допускаемое напряжение, оценить прочность материала.
9.Записать условие прочности согласно четвертой классической теории прочности (энергетической теории) и, подставив главные напряжения, допускаемое напряжение, оценить прочность материала.
17
Пример решения задачи 2
В окрестности опасной точки стальной конструкции выделен бесконечно малый элемент в виде прямоугольного параллелепипеда. На его гранях действуют нормальные и касательные напряже-
ния, равные σх = 100 МПа, σу = –50 МПа, σz = 60 МПа, τух = 40 МПа. Определить положение главных площадок, главные напряжения,
максимальные касательные напряжения и показать их; найти главные деформации и относительное изменение объема; определить удельную потенциальную энергию деформации; проверить прочность материала, используя третью и четвертую классические теории прочности, принимая [σ] = 160 МПа.
Решение. Для исследования напряженного состояния в опасной точке изобразим прямоугольный параллелепипед и действующие на его гранях напряжения (рисунок 2.2).
На площадке перпендикулярной к оси z нет касательных напряжений. Следовательно, эта площадка является главной, а σz − главным напряжением. Найдем положение двух других главных площадок, которые будут параллельны оси z:
tg 2αгл |
= − |
2τxy |
= − |
2 (− 40) |
= 0,533; |
|||||
σx |
− σy |
100 |
+ 50 |
|
||||||
|
|
|
|
|
||||||
|
αгл = |
|
1 |
arctg 2αгл =14,4D. |
||||||
|
2 |
|||||||||
|
|
|
|
|
|
|
|
|
||
Углы, определяющие положение нормалей к главным площадкам, равны
α |
гл1 |
= α |
гл |
=14,4D; |
α |
гл2 |
=α |
гл |
+90D =14,4D +90D =104,4D. |
|
|
|
|
|
|
Положение главных площадок, перпендикулярных к нормалям, показано на рисунке 2.3.
Главные напряжения, действующие на главных площадках, определяем по формуле:
18
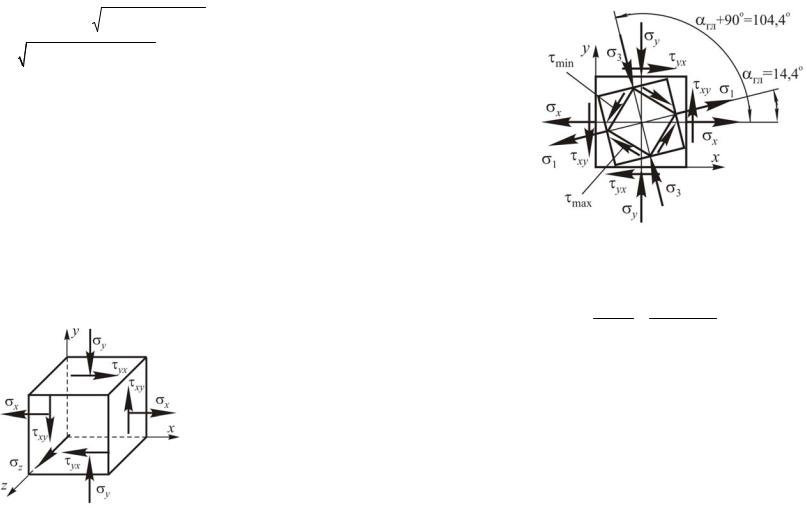
|
σminmax = |
σx + σy |
± |
1 |
|
(σx − σy )2 + 4τ2xy = |
|
|
2 |
2 |
|
||||
|
100 −50 |
± 1 |
|
|
|
||
= |
(100 +50)2 +4 (−40)2 = (25 ±85) МПа; |
||||||
|
2 |
2 |
|
|
|
|
|
|
|
σmax = 110 МПа; |
σmin = –60 МПа. |
||||
Учитывая значения σz, присваиваем σmax, σmin индексы главных напряжений:
σ1 = 110 МПа; σ2 = 60 МПа; σ3 = –60 МПа.
Заданное напряжение σу в алгебраическом смысле больше напряжения σх , поэтому площадка, на которой действует напряжение σ1 , будет определяться углом αгл2 = 104,4°. Напряжение σ1 проходит через две четверти, в которых сходятся стрелки касательных напряжений, что указывает на правильность определения направления главных напряжений σ1 и σ3 и положения главных площадок.
Рисунок 2.2 – Схема нормальных и касательных напряжений, действующих по граням элемента
19
Рисунок 2.3 – Положение главных площадок и площадок сдвига
Максимальные касательные напряжения равны:
τmax = σ1 −σ3 =110 −(−60) =85 МПа. 2 2
Площадки, на которых действуют τmax, располагаются под углом 45° к главным площадкам с напряжениями σ1 и σ3 (рисунок 2.3).
Для определения относительных линейных деформаций воспользуемся обобщенным законом Гука:
ε1 |
= |
|
1 |
|
|
[σ1 |
−μ(σ2 + σ3 )]= |
1 |
|
|
|
[110 −0,3(60 −60)]=55 10−5 ; |
||||||
E |
2 105 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ε2 |
= |
|
1 |
|
|
[σ2 |
−μ(σ1 + σ3 )]= |
|
1 |
|
|
[60 − 0,3(110 − 60)]= 22,5 10−5 ; |
||||||
E |
|
2 105 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ε |
3 |
= |
|
1 |
[σ |
3 |
−μ(σ + σ |
2 |
)]= |
|
|
1 |
[−60 −0,3(110 + 60)]= −55,5 10−5 . |
|||||
|
|
|
|
|
||||||||||||||
|
|
|
E |
|
|
1 |
2 |
105 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Находим относительное изменение объема:
θ= ε1 + ε2 + ε3 =55 10−5 + 22,5 10−5 −55,5 10−5 = 22 10−5 .
Находим удельную потенциальную энергию деформации по формуле:
20
