
- •Подставив значения (2) и (3) в формулу (1), получим:
- •МОДУЛЬ 3
- •№, тема занятия
- •Тип занятия
- •Вид занятия
- •Занятие 1
- •Знакомство с новым
- •материалом
- •Лекция
- •3 НАУЧНО-ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
- •3.1 СЛОВАРЬ ПОНЯТИЙ
- •Примеры решения задач
- •Задача 1 (уровень 2)
- •Примеры решения задач
- •Система состоит из двух тел: груза массой m, который движется поступательно, и барабана, который вращается вокруг неподвижной оси, проходящей через его центр масс (Рис 3.19).
- •Примеры решения задач
- •3.3 ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ
- •4. Механический резонанс. (Исследовать зависимость амплитуды и начальной фазы вынужденных колебаний от частоты вынуждающей силы. Дать определение механического резонанса, построить резонансные кривые.)
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА И ПРОДОВОЛЬСТВИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
КАФЕДРА ФИЗИКИ И ХИМИИ
И.Т. Неманова С.Л. Быкова
МЕХАНИКА
Учебно-методический комплекс по дисциплине «ФИЗИКА»
Часть I
МИНСК
2006
УДК 531(07) ББК 22.2я7 Н 50
Рекомендовано научно-методическим советом БГАТУ
Протокол № 6 от 28 июня 2006 г.
Авторы: канд. физ.-мат. наук, доц. И.Т. Неманова, ст. преподаватель. С.Л. Быкова
Рецензент — канд. техн. наук, доц. В.Т. Ветрова
Неманова, И.Т.
Н 50 Механика : учеб.-метод. комплекс : Ч. I / И.Т. Неманова, С.Л. Быкова. — Минск : БГАТУ, 2006.— 272 с.
ISBN 985-6770-13-0
ISBN 985-6770-12-2
УДК 531(07) ББК 22.2я7
ISBN 985-6770-13-0 |
© И.Т. Неманова, С.Л. Быкова, 2006 |
ISBN 985-6770-12-2 |
© БГАТУ, 2006 |
2
МОДУЛЬ 0
ВВЕДЕНИЕ В КУРС ФИЗИКИ
Комплексная цель. Студент должен:
а) ознакомиться
–с предметом физики и ее связью с другими науками, с целью ее изучения,
–со структурой изучаемого курса и требованиями к организации и результатам обучения,
–с математическими операциями, необходимыми для изучения курса физики;
б) уметь
– использовать математические знания в изучении курса физики,
– проводить лабораторный эксперимент и обрабатывать его результаты.
1 УЧЕБНО-ИНФОРМАЦИОННАЯ МОДЕЛЬ МОДУЛЯ
№, тема занятия |
Тип занятия |
Вид занятия |
Кол-во часов |
|
|
|
на 1 занятие |
Занятие 1 |
Знакомство |
Лабораторное |
2 |
Введение в курс |
с новым |
занятие |
|
физики |
материалом |
|
|
2НАУЧНО-ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
2.1ПРЕДМЕТ ФИЗИКИ И ЕЕ СВЯЗЬ С ДРУГИМИ НАУКАМИ
Физика изучает объективные свойства окружающего нас мира, наиболее общие формы движения материи и их взаимные превращения.
Известно, что развитие науки и техники определяется экономическими потребностями общества. Технический уровень производства в значительной степени зависит от состояния науки. История развития науки и техники показывает, какое большое значение имели открытия в физике для создания и развития новых отраслей техники. Физика явилась научным фундаментом для электронной и вычислительной техники, приборостроения, космической техники, медицинской техники и т.д.
На основе достижений физической науки разрабатываются принципиально новые методы производства, приборы и установки.
3
В свою очередь, техника оказывает большое влияние на прогресс физики. Известно, что именно технические потребности общества привели в свое время к развитию механики, необходимой для строительства сооружений. Задача создания более экономичных тепловых двигателей вызвала быстрое развитие термодинамики. Эти примеры можно продолжать.
Физика образует прочный фундамент всего естествознания, теория и эксперимент физической науки позволили за последнее десятилетие обеспечить прогресс в развитии таких наук, как биология, химия, медицина, компьютерная и лазерная техника, энергетика и др.
Высокий уровень систематизации физических знаний, логическое совершенство основных теорий, глубокое проникновение в нее математики позволяют считать физику эталоном естественнонаучных знаний. В современных условиях физика оказывает глубокое влияние на социальные, эстетические и мировоззренческие взгляды людей.
Из сказанного вытекает, что учебная дисциплина «Физика», представляющая собой совокупность физических знаний и умений, выполняет важнейшие общеобразовательные и воспитательные функции.
При изучении физики создается основа для понимания и сознательного глубокого изучения таких наук, как теплотехника, электротехника, сопротивление материалов, материаловедение и др. Например, теоретическая механика использует законы динамики движения тел, теплотехника — законы термодинамики, ТОЭ — законы электромагнетизма (на основе закона электромагнитной индукции работают электрические машины).
Исходя из этого, сформулируем роль курса физики в техническом вузе:
1.Обеспечивает строго познавательное, цельное изложение физической картины мира.
2.Является базовой дисциплиной для большого числа общенаучных, общепрофессиональных и специальных дисциплин.
Любая отрасль современного производства тесно переплетается с физикой, поэтому инженер любого профиля должен владеть физикой в такой степени, чтобы со знанием дела применять ее в своей производственной деятельности.
2.2 СОДЕРЖАНИЕ ДИСЦИПЛИНЫ «ФИЗИКА»
Курс физики рассчитан на три семестра, в каждом из которых изучаются определенные части физической науки: часть I (первый семестр изучения) — механика, молекулярная физика и термодинамика; часть II (второй семестр) — электродинамика; часть III (третий семестр) — оптика, атомная физика, ядерная физика.
Успешное усвоение материала, предусмотренного рабочей программой на каждый семестр обучения, возможно только при регулярной работе студента над каждым разделом: разбор теоретического материала, его применение при решении задач и выполнении лабораторных работ. Для поэтапного
4
изучения вопросов программы и контроля над этим процессом материал каждого семестра делится на определенные части — модули. Каждый модуль охватывает материал темы программы или нескольких близких тем. Модули учебно-методического комплекса (УМК) по модулю содержат все необходимые учебные, методические и контрольные материалы для изучения соответствующих вопросов рабочей программы.
I часть курса общей физики — «Механика. Молекулярная физика. Термодинамика» состоит из следующих модулей:
М0 — Введение в курс физики.
М1 — Кинематика материальной точки.
М2 — Динамика материальной точки и поступательного движения твердого тела. Работа и механическая энергия.
М3 — Динамика вращательного движения твердого тела. М4 — Колебательное движение.
М5 — Основы молекулярно-кинетической теории. М6 — Первое начало термодинамики.
М7 — Второе начало термодинамики. М8 — Реальные газы. Фазовые переходы.
II часть курса физики — «Электродинамика» состоит из следующих модулей:
М1 — Электрическое поле в вакууме. М2 — Электрическое поле в диэлектриках.
М3 — Проводники в электрическом поле. Энергия системы зарядов, заряженных проводников и электрического поля.
М4 — Постоянный электрический ток.
М5 — Магнитное поле постоянного электрического тока в вакууме. М6 — Магнитное поле в веществе.
М7 — Электромагнитная индукция. Основы теории электромагнитного поля.
III часть курса физики — «Оптика. Атомная физика» состоит из следующих модулей:
М1 — Упругие и электромагнитные волны.
М2 — Интерференция света. Дифракция света. Поляризация света. М3 — Квантовая природа электромагнитного излучения.
М4 — Элементы атомной физики и квантовой механики.
М5 — Элементы квантовой статистики и зонной теории твердых тел. МR — Заключение.
Врезультате изучения физики студент должен:
–знать сущность физических явлений и законов, единицы измерения основных физических величин;
–уметь применять физические законы к решению практических задач;
5
–анализировать и применять полученные знания к общеинженерным и специальным дисциплинам.
Для успешного усвоения курса студент должен:
–посещать все виды аудиторных занятий (лекции, практические и лабораторные занятия);
–посещать специально проводимые дополнительные занятия (консультации и т.п.);
–вовремя выполнять все виды самостоятельных заданий;
–систематически готовиться к занятиям и в соответствии с графиком сдавать модули.
2.3 ВЕКТОРЫ И ДЕЙСТВИЯ НАД НИМИ, ИСПОЛЬЗУЕМЫЕ В КУРСЕ ФИЗИКИ
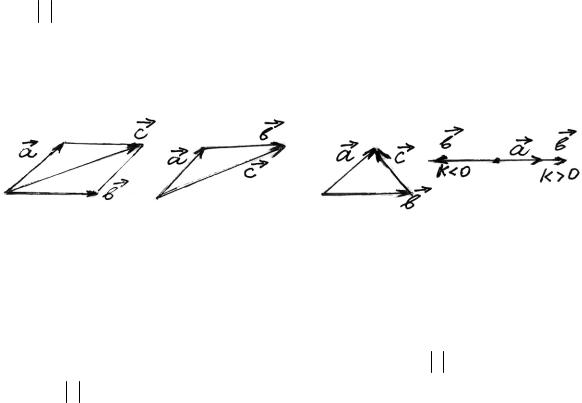
Векторами называются величины, характеризующиеся численным значением и направлением и, кроме того, складывающиеся по правилу параллелограмма. Последнее замечание существенно, так как существуют величины, также характеризующиеся численным значением и направлением, но не подчиняющиеся правилу параллелограмма при сложении, например псевдовекторы (см. далее). Вектор изображается стрелкой, обозначается буквойr со стрелкой наверхуr либо жирным шрифтом. Например, вектор скорости υ, вектор ускорения υ или a.
Численное значение вектора называется его модулем. Модуль обозначается ar либо a .
Сложение векторов: cr = ar +b , проводится по правилу параллелограмма (рис. 0.1) или, пристраивая второй вектор к концу первого, а затем соединяя вектором начало первого вектора с концом второго (рис. 0.2).
Рис. 0.1 Рис. 0.2 Рис. 0.3 Рис. 0.4
Разностью двух векторов ar −b называется такой вектор cr, который в |
|
сумме с вектором br дает вектор ar (рис. 0.3). |
|
Умножение вектора на скаляр. В результате умножения вектора av на |
|
скаляр k |
получается вектор b = ka , модуль которого в k раз больше модуля |
a , т.е. b |
= k a ; направление вектора b совпадает с направлением вектора a , |
6

если k > 0 , и направление вектора b противоположно направлению вектора ar, если k < 0 (рис. 0.4).
Проекция вектора. Рассмотрим некоторое направление в пространстве, которое зададим осью l (рис. 0.5). Пусть вектор a образует с выбранной осью угол ϕ. Величина
al = a cosϕ
называется проекцией вектора a на ось l . Это величина алгебраическая: если вектор образует с осью острый угол, то проекция положительная, если тупой — отрицательна.
Векторной проекцией, или составляющей вектора по данной оси
называется вектор
al = a cosϕe ,
где erединичный вектор вдоль оси l , e =1.
Если выбрана декартова прямоугольная координатная система X, Y, Z, по осям которойr соответственно направлены единичные векторы (базисные
орты) ir, rj,k , то вектор ar через проекции по осям системы координат запи-
шется в виде (рис. 0.6):
ar = axi + ay j + az k .
Скалярное произведение векторов. Два вектора ar и b можно умно-
жить друг на друга двумя способами: один приводит к скалярной величине, другой — к некоторому новому вектору.
Скалярным произведением векторов называется скаляр, равный произведению модулей этих векторов на косинус угла α между ними:
ar b = arb = abcosα.
В этом выражении приведены два возможных способа обозначения скалярного произведения.
Скалярное произведение взаимно перпендикулярных векторов равно
нулю ( α = π ).
2
Квадрат вектора является скалярным произведением вектора самого на
себя:
ar2 = ar ar = a a cos0 = a2 ,
т.е. квадрат вектора есть квадрат его модуля.
r |
Векторным произведением векторов a и b называется такой вектор |
c |
, |
|
cr = ar×b , |
модуль которого
c = absin α,
направлениеr которого перпендикулярно плоскости, в которой лежат векторы ar,b , и который находится по правилу правого винта (буравчика). Это прави-
7
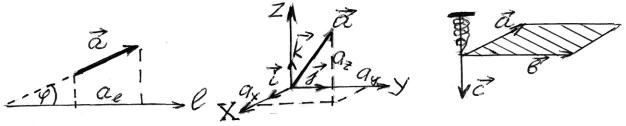
ло реализуется следующим образом: мысленно поставим правый винт перпендикулярно плоскости векторов ar,b и будем вращать его в направлении от вектора ar к вектору br по минимальному углу (рис. 0.7).
Рис. 0.5 |
Рис. 0.6 |
Рис. 0.7 |
Следует отметить, что вектор c , являющийся векторным произведением двух других векторов, отличается по своим свойствам от «обычных» векторов (типа скорости, ускорения, силы). Такие векторы, являющиеся результатом векторного умножения двух других векторов, называются псевдовекторами. Различия в свойствах проявляются в случае замены правовинтовой системы координат на левовинтовую.
Псевдовекторами являются такие физические величины, как угловая скорость, момент силы, момент импульса. В дальнейшем не будет проводиться различия между векторами и псевдовекторами.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Что изучает физика?
2.Приведите примеры использования законов физики в общеинженерных дисциплинах
3.Как определить модуль и направление векторного произведения двух векторов?
8
МОДУЛЬ 1
КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ АБСОЛЮТНО ТВЕРДОГО ТЕЛА
Комплексная цель. Студент должен:
а) знать (описывать и формулировать) понятия и определения материаль-
ной точки, абсолютно твердого тела, поступательного и вращательного движений, системы отсчета, радиуса-вектора, средней и мгновенной скорости, пути, среднего и мгновенного ускорения, тангенциального и нормального ускорений, угловой скорости и углового ускорения;
б) доказывать (получать) и характеризовать аналитические выражения для тангенциального и нормального ускорений, связь между линейной и угловой скоростью, линейным ускорением и угловым ускорением; величинами пути и скорости при произвольном движении материальной точки; в) моделировать и прогнозировать различные случаи криволинейного
движения материальной точки;
г) уметь
–конспектировать,
–применять математические знания к описанию движения материальной точки,
–применять полученные теоретические знания к решению прямых и обратных задач кинематики;
–проводить лабораторный эксперимент по измерению кинематических
величин и обрабатывать результаты эксперимента.
Преподаватель должен формировать социально-личностные качества студента: организованность, трудолюбие.
1 ВВЕДЕНИЕ. БАЗОВЫЕ ПРОБЛЕМЫ МОДУЛЯ
Механическое движение как простейшая форма движения материи. Представления о свойствах пространства и времени, лежащие в основе классической механики. Физические модели: материальная точка, абсолютно твердое тело. Поступательное и вращательное движения твердого тела. Система отсчета. Траектория. Длина пути. Вектор перемещения. Вектор мгновенной скорости. Формула для расчета пути, пройденного материальной точкой, по известному закону изменения ее скорости. Вектор мгновенного ускорения. Нормальное и тангенциальное ускорения. Угловая скорость. Угловое ускорение. Связь между линейными и угловыми величинами.
9
2 УЧЕБНО-ИНФОРМАЦИОННАЯ МОДЕЛЬ МОДУЛЯ
|
№, тема занятия |
Тип занятия |
Вид занятия |
Кол-во часов |
||
|
|
|
|
|
|
на 1 занятие |
|
Занятие 1 |
|
|
|
|
|
Кинематика |
материальной |
Знакомство |
Лекция |
2 |
||
точки и вращательного дви- |
с новым материалом |
|
|
|||
жения |
абсолютно |
твердого |
|
|
|
|
тела |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Занятие 2 |
|
|
|
|
|
Кинематика |
материальной |
Углубление, |
Практическое |
2 |
||
точки и вращательного дви- |
обобщение |
занятие |
|
|||
жения |
абсолютно |
твердого |
|
|
|
|
тела |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Занятие 3 |
|
|
|
|
|
Изучение |
кинематических |
Обобщение, |
Лабораторное |
2 |
||
величин и связи между ними |
систематизация, |
занятие |
|
|||
при поступательном и враща- |
предварительный |
|
|
|||
тельном движении |
твердого |
контроль |
|
|
||
тела |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Занятие 4 |
|
|
|
|
|
Вычисление пути, пройден- |
Углубление, |
Управляемая само- |
1 |
|||
ного |
материальной |
точкой |
обобщение, |
стоятельная работа |
|
|
в общем случае и в случае |
систематизация |
студентов |
|
|||
равнопеременного движения |
|
|
|
|||
|
|
|
|
|
|
|
|
Занятие 5 |
|
Суммарный |
|
1 |
|
Кинематика |
материальной |
контроль |
|
|
||
точки |
и |
поступательного |
|
|
|
|
движения твердого тела |
|
|
|
|||
3НАУЧНО-ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
3.1СЛОВАРЬ ПОНЯТИЙ
3.1.1Новые понятия
1.Материальная точка — это тело, размерами которого можно пренебречь в условиях данной задачи.
2.Система отсчета — это совокупность тела отсчета, относительно которого наблюдается движение материальной точки (тела), связанных с телом отсчета системы координат и часов.
3.Радиус-вектор материальной точки — это вектор, проведенный из нача-
ла координат системы отсчета в точку пространства, где в данный момент времени находится материальная точка.
10
4.Траектория материальной точки — это последовательность положений материальной точки в пространстве.
5.Вектор перемещения материальной точки — это вектор, соединяющий два последовательных положения материальной точки на траектории.
6.Путь, пройденный материальной точкой, — это длина участка траекто-
рии.
7.Средняя скорость материальной точки за некоторый промежуток времени — это отношение вектора перемещения, соответствующего данному промежутку времени, к его величине.
8.Мгновенная скорость (вектор мгновенной скорости или скорость) ма-
териальной точки — это производная радиуса-вектора материальной точки по времени.
9.Среднее ускорение материальной точки за данный промежуток вре-
мени — это отношение изменения вектора скорости за этот промежуток времени к величине этого промежутка времени.
10.Мгновенное ускорение (вектор мгновенного ускорения или ускоре-
ние) материальной точки — это производная вектора скорости по времени или вторая производная радиуса-вектора по времени.
11.Тангенциальное ускорение — это часть ускорения материальной точки, определяющая изменение величины скорости.
12.Нормальное ускорение — это часть ускорения материальной точки, определяющая изменение направления скорости.
13.Абсолютно твердое (твердое) тело — тело, расстояние между любыми двумя точками которого всегда остается постоянным.
14.Поступательное движение твердого тела — это такое движение, при котором любая прямая, проведенная в теле (на теле) остается параллельной самой себе.
15.Мгновенная угловая скорость (угловая скорость) твердого тела при его вращении вокруг неподвижной оси — это вектор (псевдовектор), вели-
чина которого равна производной угла поворота тела по времени и направление которого определяется по правилу правого винта по отношению к направлению вращения.
16.Мгновенное угловое ускорение (угловое ускорение) твердого тела при его вращении вокруг неподвижной оси — это производная вектора угловой скорости по времени.
11
3.2ОСНОВНОЙ ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
3.2.1Кинематика материальной точки
ивращательного движения абсолютно твердого тела
3.2.1.1 Механическое движение как простейшая форма движения материи
Физика изучает наиболее общие формы движения материи, свойственные как живой, так и неживой природе. Самой простой формой движения материи является механическое движение, законы которого составляют часть физики — механику. Механическое движение — это передвижение тел или частей тел в пространстве с течением времени относительно других тел. Механика состоит из двух частей: кинематики и динамики. Кинематика — раздел механики, в котором изучается движение тел без учета причин, обусловливающих это движение. В динамике изучается движение тел вместе с причинами, его вызывающими.
Механика как наука возникла еще в древнем мире. Она была в основном завершена трудами Галилея и Ньютона в XVII столетии и носит название классической, или ньютоновской механики. В начале XX столетия в результате исследований Эйнштейна была создана релятивистская механика, или специальная теория относительности, которая является механикой тел, движущихся со скоростями, близкими к скорости света в вакууме (с ≈ 3×108 м/с). Вместе с тем, в первой половине XX века исследования многих ученых привели к созданию квантовой механики, законам движения которой подчиняются микрочастицы (элементарные частицы, в определенных условиях — атомы). Обе новые механики — релятивистская и квантовая — содержат в себе классическую механику в качестве частного случая, а именно — при условии движения макротел со скоростями гораздо меньшими скорости света. Другими словами, классическая (ньютонова) механика рассматривает механическое движение тел, состоящих из огромного количества микрочастиц со скоростями намного меньшими скорости распространения света в вакууме.
Механическая система — это совокупность тел, выделенных для рассмотрения их движения.
Для определения положения механической системы в пространстве необходимо выбрать тело (или тела), по отношению к которым определяется положение механической системы в каждый момент времени. Это тело (или тела) называется телом отсчета. Чтобы точно отмечать положения механической системы в пространстве, с телом отсчета неподвижно связывают систему координат. Будем пользоваться прямоугольной декартовой системой координат. Тело отсчета, система координат и часы, с помощью которых отсчитываются промежутки времени, вместе составляют систему отсчета.
Классическая механика создана на основе представлений об абсолютном пространстве и абсолютном времени. Абсолютность пространства означает, что расстояние между определенными точками в пространстве одина-
12
ковое относительно (с точки зрения) разных систем отсчета (имеется в виду, что расстояние измеряется в одних и тех же единицах, например в метрах). Абсолютность времени означает, что промежуток времени между двумя определенными событиями одинаков в разных системах отсчета. Другими словами, абсолютность пространства и времени означает, что их свойства не зависят от выбора системы отсчета. Кроме того, в классической механике считается, что пространство, в котором происходит движение тел, является: однородным — это значит, что все точки пространства равноправные (нет выделенных точек); изотропным — это значит, что все направления в пространстве равноправные (нет выделенных направлений); трехмерным. Принимается также, что время имеет следующие свойства: оно однородно; направлено из прошлого в будущее; одномерно.
Простейшей механической системой является материальная точка. Материальная точка — это тело, размеры которого в данных условиях задачи можно не учитывать. Очевидно, что одно и то же тело в условиях одной задачи можно считать материальной точкой, а в условиях другой задачи — нельзя. Например, Земля при рассмотрении ее движения в космическом пространстве может быть принята за материальную точку. Но, если рассматривать движение тел по поверхности Земли, надо учитывать ее протяженность.
Простейшим и идеализированным случаем протяженных тел является абсолютно твердое тело. Твердое (абсолютно твердое) тело — это такое тело, в котором расстояния между произвольными точками тела не изменяются, несмотря на действия со стороны других тел. Простейшим видом механического движения твердого теля является поступательное движение. Это такое движение, при котором каждая прямая линия, проведенная через две произвольные точки тела, остается параллельной самой себе. Отсюда следует, что все точки твердого тела, движущегося поступательно, движутся одинаково, описывают одинаковые линии, смещенные одна относительно другой в пространстве (рис. 1.1, а). Другим простейшим видом движения твердого тела является вращение тела вокруг неподвижной оси, когда все точки те-
ла, кроме лежащих на оси вращения, движутся по окружностям с центрами, лежащими на этой оси (рис. 1.1, б).
Произвольное движение твердого тела можно представить в виде последовательности поступательных движений тела и вращений вокруг осей, проходящих через определенные точки. На рис. 1.2 показано, как тело из положения 1 можно перевести в положение 2: сначала тело поступательно перемещается в промежуточное положение 1′, а затем путем поворота около неподвижной оси, проходящей через точку В, в окончательное положение 2.
13
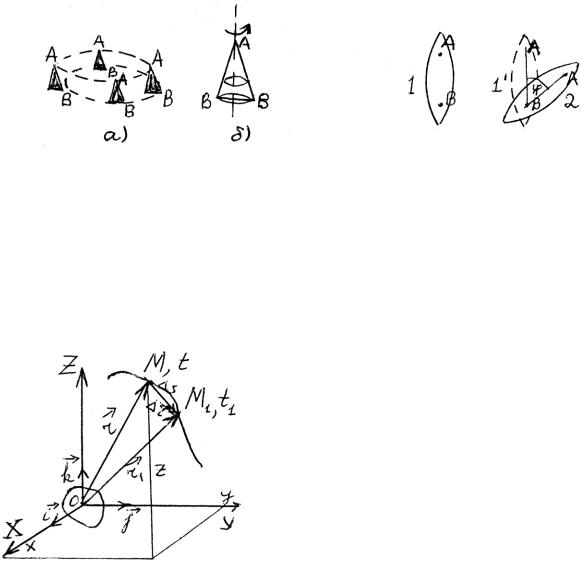
Рис. 1.1 |
Рис. 1.2 |
Изучение отмеченных простейших видов механического движения начнем с рассмотрения кинематики материальной точки.
Линия, описываемая материальной точкой при ее движении в пространстве, называется траекторией. Если траектория представляет собой прямую линию, движение называется прямолинейным, если кривую — кри-
волинейным.
Пусть материальная точка движется по определенной траектории, и мы выбрали систему отсчета, по отношению к которой наблюдаем за движением материальной точки (рис. 1.3). Положение материальной точки в каждый момент времени будем характеризовать радиусом-вектором материальной точки. Это вектор r , проведенный из начала системы координат О в точку, где находится материальная точка в момент времени t.
Во время движения материальной точки по траектории ее радиус-вектор в общем случае изменяет величину и направление; в момент времени t1, когда материальная точка
находится в точке М1 на траектории, радиус-вектор материальной точки rr1 , в момент t2 – rr2 и т.д. Это означает, что радиус-вектор материальной точки
есть функция времени, rr = rr(t) . Выберем единичные векторы ir, rj,kr (орты)
вдоль осей координат X, Y, Z соответственно. С их помощью радиус-вектор r записывается в виде векторной суммы его составляющих по осям координат:
rr = xi + yj + zk , |
(1.1) |
где x, y, z — координаты вектора r (проекции вектора r ), а значит, точки М на траектории.
Если материальная точка движется по траектории, ее координаты x, y, z изменяются, т.е. являются функциями времени:
x = x(t) , |
|
y = y(t) , |
(1.2) |
14

z = z(t) .
Равенства (1.2) представляют собой уравнение траектории в параметрическом виде (параметром является время t).
Расстояние, пройденное материальной точкой по траектории, называется путем. За промежуток времени ∆t = t1 – t материальная точка проходит путь ∆S, равной длине отрезка траектории между точками М и М1. За этот промежуток времени радиус-вектор материальной точки получил приращение
r = r1 −r. |
(1.3) |
На рис. 1.3 вектор r в соответствии с правилом сложения векторов
→
есть вектор MM1 . Этот вектор r , соединяющий положение начала и конца движения материальной точки за определенный промежуток времени, называется вектором перемещения. Модуль вектора перемещения rr при криво-
линейном движении не равен величине пути ∆S за тот же промежуток времени. Обе упомянутые величины совпадают только в случае прямолинейного движения в одну сторону. Но, если промежуток времени мал, ∆t → 0, точки М и М1 находятся близко друг от друга, и тогда
r |
|
≈ S . |
(1.4) |
|
3.2.1.2 Скорость материальной точки
Пусть материальная точка, двигаясь по траектории, находится в момент времени t в точке М, в момент времени t1 — в точке М1 (рис. 1.4). Точке М соответствует радиус-вектор r , точке М1 — r1. За промежуток времени
t = t1 – t вектор перемещения r = r1 − r .
Вектором средней скорости υñ за промежуток времени t называется
отношение вектора перемещения к промежутку времени, за который произошло это перемещение:
r |
r |
. |
(1.5) |
υñ = |
t |
||
|
|
|
Вектор υrc направлен как вектор r , т.е. вдоль хорды ММ1. Численные значения средней скорости
r |
|
|
|
rr |
|
. |
|
|
|
|
|
|
|||
υ0 |
= |
|
|
|
|
(1.6) |
|
|
|
|
|||||
|
|
t |
|
||||
|
|
|
|
|
|
|
15
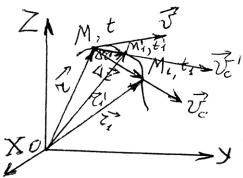
|
Уменьшим промежуток времени наблюдения |
|||||
|
за материальной точкой, т.е. рассмотрим ее |
|||||
|
движения вдоль траектории из точки М в |
|||||
|
точку М1′, в которой материальная точка ока- |
|||||
|
залась в момент времени t1′, причем t1′ < t1. |
|||||
|
Теперь за промежуток времени |
t′ = t1′ – t ма- |
||||
|
териальная |
точка |
совершила |
перемещение |
||
|
rr′ = rr1′ − rr |
( r1′ — радиус-вектор точки М1′). |
||||
|
Вектор средней скорости за промежуток вре- |
|||||
|
мени |
t′: |
|
|
|
|
r′ |
|
r′ |
. |
|
(1.7) |
|
υc = |
|
|
|
|||
t′ |
|
|
||||
|
|
|
|
|
|
|
В следующий раз возьмем еще меньший промежуток времени t" и оп- |
||||||
ределим среднюю скорость материальной точки за |
t" и т.д. Последователь- |
|||||
ность векторов средней скорости υc , υ′c , … за все меньшие промежутки вре-
мени будет стремиться к определенной векторной величине. Предел, к которому стремится вектор средней скорости материальной точки при бесконечном уменьшении промежутка времени, называется вектором мгновенной
скорости (или вектором скорости) материальной точки в момент времени t:
r |
r |
lim |
r |
. |
(1.8) |
υ = |
lim υc = |
t |
|||
|
t→0 |
t→0 |
|
|
С математической точки зрения последнее выражение представляет собой предел отношения приращения функции r (t) к приращению аргумента при условии, когда приращение аргумента стремится к нулю. Такая величина является производной функции по аргументу t. С учетом этого приходим к окончательному определению скорости материальной точки: вектор мгновенной скорости материальной точки (или вектор скорости материальной точки) в момент времени t (или в точке М) — это производная ее радиусавектора по времени:
r |
drr |
r r• |
(1.9) |
υ = |
dt |
= rt′= r . |
|
|
|
|
(В определении (1.9.) даны возможные обозначения производной по времени.)
Выясним направление υr. Когда точка М′ стремится к точке М, направление перемещения r стремится к касательной к траектории в точке М. Значит, вектор скорости υr в каждой точке траектории направлен по касательной к траектории.
Модуль вектора скорости υr, как следует из (1.8),
16

|
r |
|
|
|
r |
|
, |
|
υ |
|
= υ = lim |
|
|
|
|
|
|
|
|||||
|
|
|
t |
|
|||
|
|
|
t→0 |
|
|
||
|
|
|
|
||||
что с помощью (1.4) преобразуется следующим образом:
|
r |
|
= υ = lim |
S |
= |
dS |
. |
(1.10) |
|
|
|||||||
|
υ |
|
t |
dt |
||||
|
|
|
t→0 |
|
|
|
||
|
|
|
|
|
Таким образом, величина вектора скорости υ равна производной пути по времени.
Движение материальной точки по произвольной траектории называется равномерным, если модуль вектора скорости υ одинаков во всех точках траектории. В этом случае величина скорости равна отношению пути к соответствующему промежутку времени: υ = S/(t2 – t1).
Вектор υr имеет определенные проекции на оси координат. Чтобы их найти, воспользуемся записью радиуса-вектора r в виде суммы составляющих (1.1) и определением (1.9):
r |
drr |
|
d |
r |
r |
r |
dx r |
|
dy r |
|
dz r |
|
|||
υ = |
|
= |
|
(xi |
+ yj |
+ zk ) = |
|
i |
+ |
|
j |
+ |
|
k. |
(1.11) |
dt |
dt |
dt |
dt |
dt |
|||||||||||
Следовательно, вектор скорости υ имеет следующие проекции на оси декартовой системы координат:
υx = dx |
; |
υy = dy |
; |
υz = dz |
, |
(1.12) |
dt |
|
dt |
|
dt |
|
|
т.е. проекции вектора υr на оси координат равны производным соответствующих координат по времени.
Модуль вектора скорости
|
r |
|
= υ = |
2 |
2 |
2 |
= |
dx 2 |
dy 2 |
dz 2 |
|
|
|
||||||||||
|
υ |
|
υx |
+ υy + υz |
|
+ |
+ |
. (1.13) |
|||
|
|
|
|
|
|
|
|
dt |
dt |
dt |
|
|
|
|
|
|
|
|
|
|
|||
Рассмотрим обратную задачу: по известной зависимости модуля скорости от времени, т.е. по известной функции υ(t), найти путь, проходимый материальной точкой за определенный промежуток времени от момента t1 до момента t2. Для решения этой задачи построим график данной зависимости
υ(t) (рис. 1.5) и отметим промежуток времени |
t = t2 – t1. Разобьем этот про- |
|
межуток времени на N малых промежутков |
t1, t2, …, |
tN. На протяжении |
каждого полученного таким образом промежутка времени |
ti считаем снача- |
|
17 |
|
|

|
ла величину скорости постоянной и равной |
|
|
определенному значению υi на этом про- |
|
|
межутке. На рис. 1.5 за υi принято значение |
|
|
величины скорости материальной точки в |
|
|
начале каждого ti. При таком предположе- |
|
|
нии путь, пройденный материальной точкой |
|
|
за малый промежуток времени приблизи- |
|
|
тельно можно вычислить по простой фор- |
|
Рис. 1.5 |
муле равномерного движения: |
|
|
Si υi ti . |
(1.14) |
На графике зависимости υ(t) такое произведение численно равно площади заштрихованной полоски. Приблизительное значение пути, пройденного материальной точкой на протяжении времени t = t2 – t1, получится после суммирования выражений (1.14) по индексу i, который пробегает значения от
1 до N:
N
S ∑υi ti . (1.15)
i=1
На графике зависимости υ(t) (рис. 1.5) эта сумма численно равна площади фигуры под ломаной линией, образованной верхними сторонами полосок. Равенство (1.15) будет выполняться более точно, если выбирать меньшие промежутки ti. Предельное значение суммы при условии, когда все ti стремятся к нулю (в таком случае их количество стремится к бесконечности), точно совпадает с путем, пройденным материальной точкой за промежуток времени от t1 до t2:
N
S = lim ∑υi ti . (1.16)
t→0 i=1
Как известно, предел суммы произведений значения функции (υ есть функция t) на приращение аргумента, когда приращения аргумента стремятся к нулю, является определенным интегралом от этой функции:
t2 |
υdt. |
|
S = ∫ |
(1.17) |
|
t1 |
|
|
При ti → 0 ломаная линия графика стремится к графику υ(t), величина пути S, определенная формулой (1.17), в пределе будет равна площади криволинейной трапеции, т.е. фигуры под линией зависимости υ(t).
18

В частном случае, когда вектор скорости υ изменяется только по направлению, но остается постоянным по величине, движение равномерное, и при вычислении интеграла (1.17) приводит к
t2 |
−t1 ), |
|
S = υ∫dt = υ(t2 |
(1.18) |
|
t1 |
|
|
что следует из определения скорости равномерного движения.
3.2.1.3 Ускорение материальной точки
При произвольном движении материальной точки ее вектор скорости υ изменяет как свою величину, так и направление. Для характеристики изменения скорости вводится физическая величина — ускорение.
Пусть материальная точка движется по произвольной траектории. В момент времени t она находится в точке М и имеет скорость υr; соответственно в момент времени t1 > t, когда материальная точка занимает положение М1, она имеет скорость υr1 (рис. 1.6). За промежуток времени t = t1 – t произошло изменение скорости
υ = υ1 − υ.
Чтобы построить вектор υ, надо вектор υ1 перенести параллельно
самому себе из точки М1 в точку М. Тогда υ будет представлять собой вектор, соединяющий концы векторов υ и υ1.
Вектором среднего ускорения añ за промежуток времени t называется
отношение вектора изменения скорости к промежутку времени, за который произошло это изменение:
arc = |
υ. |
(1.19) |
|
t |
|
Подобным образом, как при введении вектора мгновенной скорости, будем уменьшать промежутки времени t, устремляя их к нулю и определяя каждый раз вектор среднего ускорения по формуле (1.19). Предел, к которому при этом будет стремиться вектор añ , называется вектором мгновенного
ускорения материальной точки (вектором ускорения) в момент времени t,
а именно:
ar = lim arñ = |
lim |
υ. |
(1.20) |
t→0 |
Β t→0 |
t |
|
19
Последнее выражение представляет собой производную вектора скорости по времени.
Таким образом, вектор мгновенного ускорения (ускорения) материальной точки в момент времени t — это производная вектора скорости материальной точки по времени:
r |
|
dυ |
|
|
a |
= |
|
. |
(1.21) |
dt |
||||
Учитывая определение скорости (1.9), вектор ускорения (1.20) можно записать в виде второй производной радиуса-вектора по времени:
r |
|
d drr |
|
d 2rr |
|
|
||
a |
= |
|
|
|
= |
dt2 |
. |
(1.22) |
|
||||||||
|
|
dt dt |
|
|
|
|
||
Вектор ускорения направлен под определенным углом к касательной траектории в данной точке. Используя определения (1.21) или (1.22), а также разложения радиуса-вектора материальной точки и ее вектора скорости, получим с учетом (1.12) разложение вектора ускорения по осям координат:
r |
|
d |
|
r |
|
r |
|
|
r |
|
dυ |
x |
r |
|
dυy |
r |
|
dυ |
z |
r |
|
a |
= |
|
(υxi +υy |
j +υzk ) |
= |
|
i |
+ |
|
j |
+ |
|
k |
= |
|||||||
dt |
dt |
|
dt |
dt |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.23) |
||||
|
d 2 x r |
d 2 y r |
|
d 2 z r |
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
dt2 |
i + |
dt2 |
j |
dt |
2 |
k , |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
что можно записать в следующем виде: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
ar = axi +ay j +azk. |
|
|
|
(1.24) |
|||||||||||
Сравнение выражений (1.23) и (1.24) приводит к следующим формулам для проекций вектора ускорения a :
ax = |
dυ |
x = |
dx2 |
; ay = |
dυy |
= |
d 2 y |
; az = |
dυ |
z = |
d 2 z |
. (1.25) |
|
|
dt2 |
dt |
at |
2 |
|
dt2 |
|||||||
|
dt |
|
|
|
dt |
|
|||||||
Наконец, для модуля вектора ускорения можно записать следующие эквивалентные выражения:
20
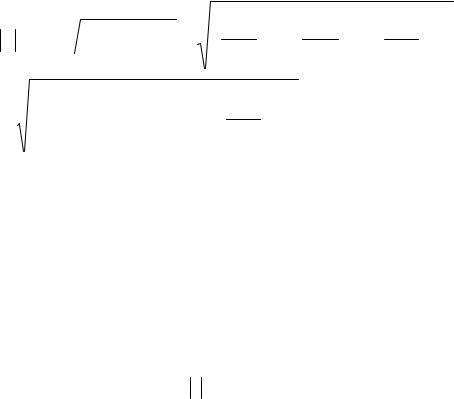
ar = a = 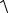 ax2 +a2y +az2 =
ax2 +a2y +az2 =
|
d 2 x |
2 r |
d 2 y 2 |
r |
||||||
= |
|
|
|
|
i |
+ |
|
|
|
j |
|
|
|
|
|||||||
|
|
dt |
2 |
|
|
dt |
2 |
|
||
|
|
|
|
|
|
|
|
|
||
dυx 2 + dυy 2 + dυz 2 =dt dt dt
(1.26)
+d 22z 2 kr.dt
3.2.1.4 Нормальное и тангенциальное ускорения
Ускорение материальной точки a определяет изменение как величины (модуля) вектора скорости υ, так и его направления. В соответствии с этим вектор ускорения a можно представить в виде суммы двух векторов таким образом, чтобы один из них учитывал изменение только величины скорости, а другой — изменение только направления скорости. Для осуществления такого разложения введем в рассмотрение единичный касательный вектор τ (его модуль равен единице, τ = 1), направленный по касательной к траекто-
рии движения материальной точки в сторону скорости в каждой точке (см. рис. 1.6, где в точке М единичный касательный вектор τ, в точке М1 — τ1 ). С
помощью этого вектора τ вектор скорости материальной точки υ в каждой
точке траекторииr |
можно записать в виде произведения модуля этого вектора |
|||
|
υ |
= υ и вектораτ: |
|
|
|
|
|
υ= υτ. |
(1.27) |
Подставив (1.27) в определение вектора ускорения материальной точки (1.21) и воспользовавшись правилом вычисления производной произведения двух функций, получим:
a = d |
(υτ) = dυ |
τ+υdτ. |
(1.28) |
||||
r |
|
r |
|
r |
|
|
|
|
dt |
|
dt |
|
dt |
|
|
В равенстве (1.28) вектор ускорения записан в виде суммы двух составляющих. Выясним смысл каждой из них.
Первое слагаемое в последнем равенстве представляет собой вектор, направленный по касательной к траектории. По этой причине он называется
касательным, или тангенциальным ускорением aτ.
r |
|
dυ |
r |
|
|
aτ |
= |
τ. |
(1.29) |
||
dt |
|||||
|
|
|
|
21
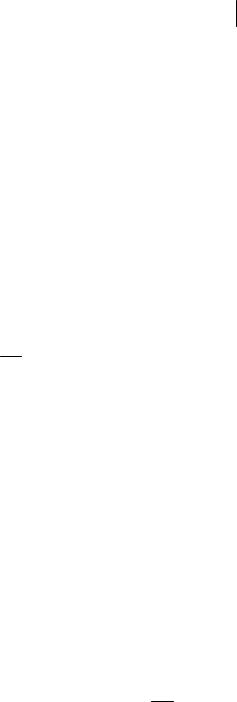
Абсолютная величина (модуль) касательного ускорения aτ, как следует из (1.29) при учете единичности τ1 ,
arτ |
|
|
dυ |
|
|
|
|
= aτ = |
|
. |
(1.30) |
||
|
||||||
|
dt |
|||||
|
|
|
|
|
||
Она полностью определяется изменением модуля вектора скорости υ.
Если модуль вектора скорости с течением времени увеличивается, dυ > 0 , dt
вектор касательного ускорения aτ направлен в ту же сторону по касательной траектории, что и вектор rτ1 , а это значит — в сторону вектора υ, то в этом случае движение материальной точки ускоренное. Если же модуль вектора
скорости с течением времени уменьшается, |
dυ |
< 0, вектор aτ |
направлен по |
||
|
|||||
|
dt |
r |
и |
υ, |
|
касательной траектории, но в сторону, противоположную векторам τ1 |
|||||
то движение материальной точки замедленное. Наконец, если модуль вектора скорости материальной точки во время движения остается постоянным,
dυ =0 , то в соответствии с (1.29) нулю равно и тангенциальное ускорение, dt
aτ= 0. Это случай равномерного движения. Таким образом, тангенциальное
(касательное) ускорение характеризует изменение модуля (абсолютной величины или величины) вектора скорости.
Рассмотрим вторую часть ускорения, которая в формуле (1.29) дается вторым слагаемым. По причинам, которые выяснятся в дальнейшем, эта часть ускорения называется нормальным ускорением an :
arn |
= υ |
dτ |
. |
(1.31) |
|
||||
|
|
dt |
|
|
Дляr определения величины и направления вектора нормального ускорения an необходимо отдельно рассмотреть производную единичного векто-
ра τ по времени ddtτ . При переходе из одной точки траектории в другую
единичный касательный вектор τ, оставаясь по модулю равным единице, изменяет, вообще говоря, свое направление вместе с касательной траекторией. Это означает, что вектор τ является функцией времени, τ = τ(t). По оп-
ределению производной функции:
dτ |
= lim |
τ |
, |
(1.32) |
dt |
å→0 |
t |
|
|
22

где τ — это изменение единичного касательного вектора τ при переходе из одной точки траектории в другую за промежуток времени t. В случае, показанном на рис. 1.6, τ = τ1 − τ, где r1 — единичный касательный вектор
в точке М1, который перенесли параллельно самому себе в точку М вместе с вектором скорости υ1 . Вектор τ на этом рисунке соединяет концы векто-
ров τ и τ1 , находящихся в точке М. Для определения модуля нормального ускорения arn , который в соответствии с (1.31) должен быть записан следующим образом:
an |
|
dτ |
|
|
|
||
= υ |
|
|
, |
(1.33) |
|||
dt |
|||||||
|
|
|
|
|
|
||
необходимо найти величину drτ . На основании (1.32) dt
|
r |
|
|
|
|
τ |
|
|
|
|
|
|
|
|
|
dτ |
= |
lim |
|
|
|
|
. |
(1.34) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
dt |
|
|
|
|
|
|
|
|
|
||||
|
|
t→0 |
|
t |
|
|
|
|
|
|||||
Модуль изменения единичного касательного вектора, т.е. |
|
τ |
|
, найдем |
||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(т.е υ и υ1 ) |
||||
следующим образом. Обозначим угол между векторами τ и τ1 |
||||||||||||||
Δϕ (рис. 1.7, а). Рассмотрим равнобедренный треугольник МАВ ( τ + τ1 = 1).
Его сторона АВ, которая представляет собой |
|
τ |
|
, может быть записана в виде: |
|||||||||
|
|
||||||||||||
АВ = |
r |
= 2ВС = 2 |
r |
|
|
|
ϕ |
|
|
|
ϕ |
|
|
τ |
τ |
×sin |
|
|
= 2sin |
|
. |
(1.35) |
|||||
|
2 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
Имея в виду то, что при переходе к производной в выражении (1.34) величины t и rτ будут стремиться к нулю и при этом угол Δϕ уменьшает-
ся, тоже стремясь к нулю, Δϕ → 0, можно считать, что Δϕ << 1. При этом условии синус угла приблизительно равен углу (имеется в виду, что угол изме-
ряется в радианах). Поэтому в выражении (1.35) будем считать sin 2ϕ 2ϕ ,
и в таком случае это выражение приобретет вид:
τ |
|
ϕ. |
(1.36) |
|
|||
|
|
|
|
23
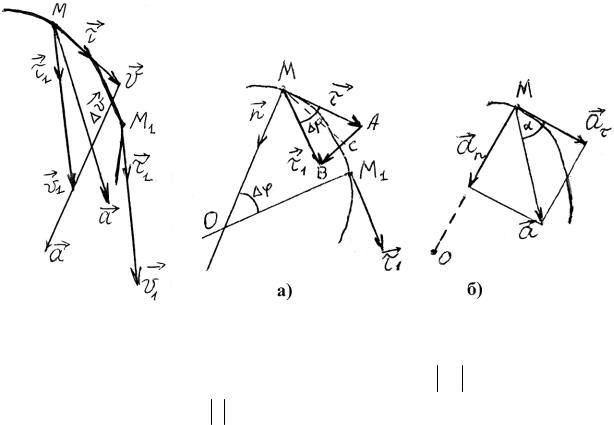
Рис. 1.6 Рис. 1.7
Тот же результат получим, рассматривая АВ = τ в качестве длины дуги окружности радиуса τ = 1, на которую опирается угол Δϕ. Тогда надо
использовать известное соотношение, что дуга окружности равна произведению ее радиуса на угол.
Для определения угла Δϕ поступим следующим образом. Проведем через точки М и М1 в плоскости рисунка прямые, перпендикулярные касательным к траектории в этих точках. Эти прямые пересекаются в точке О (рис. 1.7, а). Отрезки МО и М1О в общем случае не равны между собой. Но при условии t → 0 точка М1 → М и в пределе будет выполняться равенство МО = М1О. Предельное положение точки О при этом называется центром кривизны траектории в точке rМ. Угол МОМ1 на рис. 1.7, а равен углу Δϕ, образованному векторами τ и τ1 по признаку равенства углов со взаимно
перпендикулярными сторонами. Длина дуги ММ1 есть путь S, пройденный материальной точкой за промежуток времени t. По определению радиус кривизны R траектории в точке М — это производная длины дуги траекто-
рии S по углу ϕ, который представляет собой угол между прямыми ОМ и ОМ1, проведенными перпендикулярно траектории в точке М и близкой к ней точке, а именно:
R = lim |
S |
= dS . |
(1.37) |
ϕ→0 |
ϕ |
dϕ |
|
Определенная этой формулой величина радиуса кривизны R равна длине отрезка ОМ, R = ОМ, т.е является расстоянием между точкой траектории и центром кривизны траектории в этой точке. Можно сказать, что R — радиус
24

той окружности, с дугой которой совпадает бесконечно малая окрестность точки М на траектории.
Величина К, обратная радиусу кривизны R, называется кривизной траектории в точке М:
Ê = |
1 |
. |
(1.38) |
|
R |
||||
|
|
|
||
Из (1.37) вытекает приблизительное равенство |
|
|||
S = R |
ϕ , |
|
||
или |
S . |
|
||
ϕ |
(1.39) |
|||
|
|
R |
|
|
С учетом (1.36) получим также следующее соотношение для модуля τ :
rτ RS ,
подставив которое в выражение (1.39), найдем модуль производной единичного касательного вектора по времени в следующем виде:
r |
|
1 |
|
S |
|
1 |
|
|
|
dτ |
= |
lim |
= |
|
dS . |
||||
dt |
R |
t |
R |
||||||
|
t→0 |
|
|
dt |
Если учесть еще формулу (1.10), то последнее выражение запишется следующим образом:
dτ |
|
υ |
. |
(1.40) |
||
|
= |
|||||
dt |
|
|||||
|
|
R |
|
|||
Наконец, подставив (1.40) в (1.33), получим величину нормального ускорения:
an = |
υ2 |
. |
(1.41) |
|
R |
||||
|
|
|
Из последней формулы видно, что величина нормального ускорения в определенной точке траектории (в определенный момент времени) зависит от величины скорости материальной точки и от радиуса кривизны траектории в этой точке.
25

Выясним направление вектора an . Из его определения (1.31) следует,
что он имеет направление вектора τ в пределе, когда t → 0. При последнем условии угол между боковыми сторонами треугольника МАВ (рис. 1.7, а)
|
π |
|
r |
и его основанием стремится к значению |
2 |
, отсюда видно, что вектор |
τ в |
пределе, когда t → 0 будет направлен перпендикулярно траектории материальной точки по радиусу кривизны в сторону центра кривизны О. Таким образом, вектор нормального ускорения an имеет направление, перпендику-
лярное (нормальное) к траектории движения материальной точки, чем и объясняется его название. Введем в рассмотрение единичный вектор n , направленный в каждой точке траектории по радиусу кривизны в сторонуrцентра
кривизны, n = 1. С помощью этого вектора нормальное ускорение an можно записать следующим образом:
r |
= |
υ2 r |
|
an |
n . |
(1.42) |
|
|
|
R |
|
Полное ускорение материальной точки a , как показывает (1.24), представляет собой векторную сумму нормального и тангенциального ускорений:
a = aτ + an ,
(что показано на рис. 1.7, б), или, учитывая (1.25) и (1.42),
r |
= dυ |
r |
υ |
2 |
r |
(1.43) |
a |
τ+ |
|
n , |
|||
|
dt |
|
R |
|
|
|
где первое слагаемое учитывает изменение только величины скорости, а второе — только ее направления. Вектор ускорения a как векторная сумма направлен под определенным углом α к касательной траектории в сторону ее вогнутости. Величина этого угла зависит от величины aτи an . Векторы aτ и
an перпендикулярны друг другу, поэтому модуль вектора a определяется по теореме Пифагора:
|
r |
|
|
2 |
|
2 |
|
dυ 2 |
|
υ2 |
|
2 |
|
|
= a = |
a |
+a |
= |
. |
(1.44) |
|||||||
|
a |
|
|
|
+ |
|
|
||||||
|
|
|
|
τ |
|
n |
|
dt |
|
R |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Отметим некоторые частные случаи движения материальной точки.
1. В случае равномерного движения по произвольной траектории υ = const, aτ = 0 и вектор ускорения в каждой точке траектории
26

r = r = υ2 r a an R n .
Если, кроме того, траектория является окружностью, то радиус кривизны R во всех точках траектории одинаков и представляет собой радиус окружности. Центр кривизны всех точек окружности находится в ее центре. В этом случае нормальное ускорение называется центростремительным.
2. В случае прямолинейного движения радиус кривизны траектории (прямой линии) R → ∞, поэтому an →0 . Вектор ускорения в этом случае
есть вектор тангенциального ускорения:
|
|
r |
r |
|
dυ r |
|
|
|
|
dυ |
|
|
||
|
|
a |
= aτ |
= |
|
|
τ, |
|
a = aτ |
= |
|
|
|
. |
|
|
|
|
dt |
||||||||||
|
|
|
|
|
dt |
|
|
|
|
|
|
|||
К тому же если a = const , |
то |
имеет |
место |
|
равнопеременное движение: |
|||||||||
при |
dυ |
> 0 равноускоренное, при |
dυ |
< 0 |
— равнозамедленное. |
|||||||||
|
|
dt |
||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
||
3. Наконец, если при прямолинейном движении материальной точки
dυ =0 , то движение прямолинейное и равномерное: dt arτ = 0, an = 0 , a = 0 .
3.2.1.5 Кинематика вращательного движения
Одним из простейших движений (абсолютно) твердого тела является вращение вокруг неподвижной оси. Рассмотрим кинематические характеристики вращения тела произвольной формы около неподвижной оси ОО′ (рис. 1.8). При вращении все точки тела, кроме лежащих на оси вращения
ОО′, движутся в плоскостях, перпендикулярных оси |
|
ОО′, по окружностям определенных радиусов. Радиус |
|
каждой окружности равен расстоянию от данной точки |
|
тела до оси вращения. Точки находятся на различных |
|
расстояниях от оси вращения, имеют разные величины |
|
скорости в каждый момент времени. Поэтому враще- |
|
ние тела вокруг неподвижной оси неудобно характери- |
|
зовать вектором скорости υ его точек. Для характери- |
|
стики вращения твердого тела вокруг неподвижной |
|
оси существует специальная физическая величина — |
|
угловая скорость вращения. Она определяется сле- |
Рис. 1.8 |
дующим образом. Предположим, что за промежуток |
|
27 |
|
времени t тело повернулось вокруг неподвижной оси ОО′ на угол Δϕ (это значит, что на угол Δϕ повернулся радиус-вектор каждой точки тела, проведенный перпендикулярно ОО′).
Модуль угловой скорости тела определяется как производная угла поворота по времени:
ω= lim |
ϕ = |
dϕ |
. |
(1.45) |
|
||||
å→0 |
t dt |
|
||
Вектор угловой скорости ω направлен вдоль оси вращения ОО′ в сторону, определяемую правилом правого винта (буравчика). А именно: если поместить правый винт вдоль оси ОО′ и поворачивать его вместе с телом, то направление поступательного движения винта будет совпадать с направлением вектора угловой скорости ωr .
Скорость υr точек тела, которую называют линейной скоростью (чтобы не путать с угловой), связана с угловой скоростью вращения тела. Чтобы найти эту связь, рассмотрим определенную точку тела Мi (i — номер точки), которая во время вращения тела движется по окружности радиуса ri с определенной скоростью (линейной) υi . За элементарный промежуток времени dt
эта точка тела проходит путь dSi, равный длине дуги окружности радиуса ri с углом dϕ, на который повернулось тело вокруг оси ОО′. На основании (1.10) модуль скорости i-ой точки тела
υi = dSdti .
Но величина дуги окружности связана с углом этой дуги и ее радиусом простым соотношением: dS = rdϕ, — и линейную скорость точки тела при учете (1.45) можно записать в виде:
υ |
i |
= |
ridϕ |
= r ω . |
(1.46) |
|
|||||
|
|
dt |
i |
|
|
|
|
|
|
|
Как можно заметить на рис. 1.8, векторы ω, r , υ составляют правую тройку векторов: поворот правого винта от вектора ω к вектору rrна минимальныйr угол ведет к поступательному движению винта в направлении вектора υ; к тому же все три упомянутых вектора взаимно перпендикулярны. Основываясь на этом и принимая во внимание (1.45), можно написать связь между векторами линейной и угловой скорости определенной точки вращающегося твердого тела следующим образом:
r |
v |
(1.47) |
υ = ω×r . |
||
28

(Напомним, что векторное произведение двух векторов ar иrb — это вектор
c , величина которого c = absin α, где α — угол между ar и b , правило определения направления cvсовпадает с правилом правого винта, если его помес-
тить перпендикулярноr обоим векторам a и b и поворачивать по минимальному углу от a к b ).
Если твердое тело вращаетсяv вокруг неподвижной оси ОО′ равномерно, то угловая скорость тела ω = const. Период вращения Т — это время, за которое тело поворачивается на угол 2π. В этом случае имеем следующие простые выражения связи величин, характеризующих вращательное движение тела ( ν — частота вращения):
ω= |
ϕ |
, |
T = |
2π |
, |
1 |
= ν , |
ν = |
ω |
. |
(1.48) |
t |
ω |
T |
|
||||||||
|
|
|
|
|
|
2π |
|
||||
Для характеристики неравномерного вращения твердого тела вводится вr рассмотрение вектор углового ускорения. Вектором углового ускорения
β называется вектор, равный производной угловой скорости по времени:
r |
dω |
(1.49) |
||
β = |
|
|
||
dt |
||||
|
|
|||
При неподвижной оси вращения вектор углового ускорения β направлен вдоль оси вращения, а именно: так же, как вектор ω, при ускоренном
вращении ( ddtω > 0), и в сторону, противоположную вектору ω, при замед-
ленном вращении ( ddtω < 0).
Точки тела, вращающегося вокруг неподвижной оси, в общем случае имеют как нормальное, так и тангенциальное ускорение. Величина тангенциального ускорения aτ связана с величиной углового ускорения β. Действи-
тельно, на основании равенств (1.30) и (1.46) имеем следующее выражение: aτ = ddtυ = d (dtωr) .
В твердом теле расстояние r между каждой точкой тела и осью вращения не изменяется, поэтому в последнем выражении величину r можно вынести из-под знака производной. С учетом этого и (1.49) получим:
aτ = r |
dω |
|
= rβ . |
(1.50) |
|
dt |
|||||
|
|
|
|||
29
Величина нормального ускорения an точек вращающегося тела связана
с угловой скоростью тела. Действительно, из (1.41) и (1.46) |
вытекает сле- |
|||
дующее равенство: |
υ2 |
|
|
|
an = |
= ω2r |
(1.51) |
|
|
r |
|
|||
|
|
|
|
|
Сравнивая направления векторов r , ω, aτ , an , β, можно прийти к выводу, что векторная запись выражений (1.50) и (1.51) имеет следующий вид:
r r |
r |
r |
2 r |
(1.52) |
aτ =β×r , |
an = −ω r . |
|||
4 МАТЕРИАЛЫ, ИСПОЛЬЗУЕМЫЕ В ПРОЦЕССЕ ОБУЧЕНИЯ
4.1 МАТЕРИАЛЫ К ЛЕКЦИИ
Лекция 1 «Кинематика материальной точки и вращательного движения абсолютно твердого тела»
План лекции
1.Механическое движение как простейшая форма движения материи (предварительные определения, радиус-вектор, перемещение).
2.Скорость материальной точки (средняя скорость, предельный переход
кмгновенной скорости, ее компоненты и величина, вычисление пути по заданной зависимости величины скорости от времени).
3.Ускорение материальной точки (среднее ускорение, предельный переход
кмгновенному ускорению, компоненты, величина).
4.Нормальное и тангенциальное ускорения (разложить вектор ускорения на нормальную и тангенциальную части, получить окончательные векторные выражения).
5.Кинематика вращательного движения (средняя угловая скорость, мгновенная угловая скорость, среднее угловое ускорение, мгновенное угловое ускорение). Связь линейных и угловых скоростей и ускорений.
Контрольные вопросы
1.В каком случае величина вектора перемещения совпадает с величиной пути?
2.При каком движении материальной точки величина средней скорости совпадает с величиной мгновенной скорости в каждый момент времени?
3.Центростремительное ускорение при движении точки по окружности является нормальным или тангенциальным?
30
4. Чему равно тангенциальное ускорение при равномерном движении материальной точки?
Вопросы для самоконтроля
Iуровень (репродуктивный)
1.Что такое механическая система, система отсчета, материальная точка, траектория материальной точки?
2.Какие свойства пространства и времени положены в основу классической механики?
3.Какое движение тела называется поступательным, вращательным?
4.Как определяется радиус-вектор материальной точки, вектор перемещения, путь, вектор средней скорости материальной точки?
5.Что такое вектор (мгновенной) скорости материальной точки? Как он направлен?
6.Как вычислить путь, пройденный материальной точкой, если известен закон изменения величины ее скорости в зависимости от времени?
7.Как определяется среднее ускорение материальной точки, ее мгновенное ускорение (ускорение)?
8.По какому принципу ускорение делится на тангенциальную и нормальную составляющие? Чему равна и как направлена каждая из них?
9.Что такое радиус кривизны траектории в данной точке?
10.Как определяется вектор угловой скорости тела, вращающегося вокруг неподвижной оси (или материальной точки, движущейся по окружности)? Каково его направление?
11.Какова связь векторов угловой и линейной скорости для точки, движущейся по окружности?
12.Как определяется вектор углового ускорения? Каково его направление?
13.Какова связь между тангенциальной и нормальной составляющими ускорения и угловыми ускорением и скоростью?
IIуровень (продуктивный)
1.Как получить формулу для вычисления пути, пройденного материальной точкой, если известен закон изменения ее скорости? Каков геометрический смысл величины пути?
2.Каким образом можно разделить ускорение материальной точки на тангенциальную и нормальную составляющие? Как направлено тангенциальное ускорение в различных случаях движения? При каком движении оно равно нулю?
31

3.Как получить окончательное выражение для нормальной составляющей ускорения (в векторном виде)? В каких случаях движения оно равно нулю? Объяснить понятия радиуса кривизны траектории и центра кривизны.
4.Как найти связь между линейной и угловой скоростями материальной точки, движущейся по окружности (в векторном виде)?
5.Как найти связь между тангенциальным ускорением точки, движущейся по окружности, и угловым ускорением; между нормальным ускорением и угловой скоростью (в векторном виде)?
III уровень (творческий)
1.Как найти кинематические уравнения движения (зависимость координат от времени) в таких случаях криволинейного движения материальной точки, как движение по винтовой линии, движение точки катящегося колеса, движение в поле силы тяжести при наличии невертикального ускорения?
2.Как определить в указанных выше случаях скорость, ускорение, радиус кривизны траектории, угол между скоростью и ускорением в зависимости от времени?
4.2МАТЕРИАЛЫ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ
4.2.1КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ
ИВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
4.2.1.1Радиус-вектор. Путь. Вектор перемещения. Уравнение траектории
Примеры решения задач
Задача 1 (уровень 1)
Определить уравнение траектории материальной точки, радиус-вектор которой относительно начала координат изменяется с течением времени по
закону:
rr = 2ti +8t2 j .
Дано:
rr = 2tir +8t2 rj
y = f (x) — ?
Решение:
Запишем выражение для радиус-вектора r в общем виде: rr(t) = xi + yj + zk .
Сравнивая данное в задаче выражение для r и выражение в общем виде, получим:
32
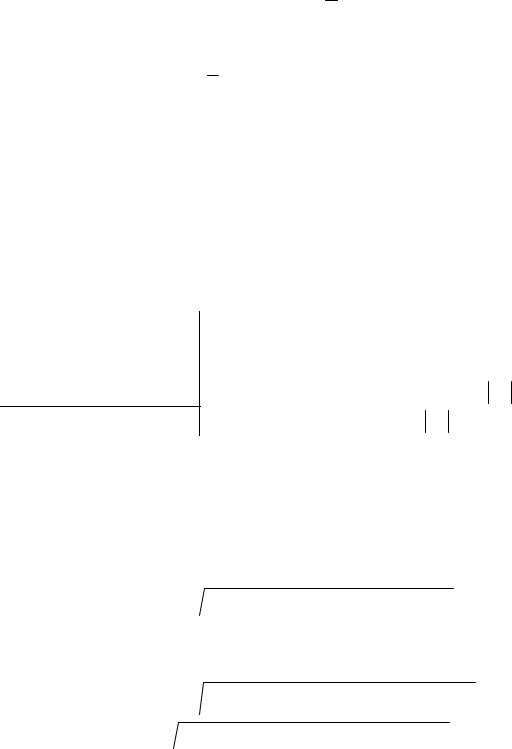
x = 2t , |
(1) |
y = 8t2 , |
(2) |
z = 0 .
Выразим из (1) t :
t = 2x
и подставим в (2):
y=8 x 2 = 2x2 — уравнение параболы.
2
Ответ: траектория описывается уравнением y = 2x2 , имеет вид параболы.
Задача 2 (уровень 2)
Прямолинейное rдвижение материальной точки описывается уравнением: rr = 3t2ir + 4t2 rj +8tk . Определить путь, пройденный материальной точкой за время от t1 = 1 с до t2 =4 с.
Даноr :2 r 2 r r r = 3t i + 4t j +8tk
t1 = 1 с; t2 = 4 c
S — ?
Решение:
При прямолинейном движении в одном направлении (так как координаты x, y, z увеличиваются) путь S
равен длине вектора перемещения. rr :
S = r .
Материальная точка в момент времени t1 находится в точке M1 (x1, y1, z1 ) , а в
момент времени t2 |
— в точке M2 (x2 , y2 , z2 ) . |
|||||||||||||||
Тогда S = |
|
rr |
|
= |
|
rr |
(t |
2 |
)−r |
(t ) |
|
. |
||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
1 |
1 |
|
|
|||
Длина вектора |
|
rr |
|
|
, а следовательно, и путь, пройденный материальной точ- |
|||||||||||
|
|
|||||||||||||||
кой,
S=  (x2 − x1 )2 +(y2 − y1 )2 +(z2 − z1 )2 , x1 = 3t12 , y1 = 4t12 ,z1= 8t1 ,
(x2 − x1 )2 +(y2 − y1 )2 +(z2 − z1 )2 , x1 = 3t12 , y1 = 4t12 ,z1= 8t1 ,
x2 = 3t22 , y2 = 4t22 ,z2 = 8t2 ,
S=  (3t22 −3t12 )2 +(4t22 −4t12 )2 +(8t2 −8t1 )=
(3t22 −3t12 )2 +(4t22 −4t12 )2 +(8t2 −8t1 )=
=  9(42 −12 ) +16(42 −12 ) + 64(4 −1)278,75 м.
9(42 −12 ) +16(42 −12 ) + 64(4 −1)278,75 м.
Ответ: S = 78,75 м.
33

|
|
Аудиторные задачи |
||
1 |
(уровень 2). С башни высотой h = 30 м в горизонтальном направлении |
|||
брошено тело с начальной скоростью |
υ0 =10 м/с. Определить уравнение |
|||
траектории тела. y = h − |
g |
x2. |
|
|
|
|
|||
|
|
2υ02 |
|
|
|
|
|
|
|
2 |
(уровень 2). Материальная точка движется в плоскости XY. Это движение |
|||
описывается зависимостями: |
x = 3sin ωt |
и y = 3cosωt . Записать уравнение |
||
траектории точки. Найти зависимость пройденного точкой пути от времени, считая, что при t = 0 S = 0. [Окружность x2+y2 = 9; S=3ωt.]
4.2.1.2Скорость материальной точки
Примеры решения задач
Задача 1 (уровень 1)
Тело движется вдоль оси x по закону: x = A + Bt + Ct3, где A = 3 м; B = 2,5 м/с; C = 0,25 м/с3. Определить среднее значение скорости за промежуток времени от t1 = 1 c до t2 = 6 c.
Дано:
х = A + Bt + Ct3
A = 3 м
B= 2,5 м/с
C= 0,25 м/с3
t1 = 1 с t2 =6 c
υñð — ?
Решение: Из определения средней скорости:
r
υñð = rt = St
В нашем случае тело движется вдоль оси x, т.е. изменяется одна координата:
|
|
|
|
|
|
|
υñð = |
|
x |
= |
x(t2 )− x(t1 ) |
; |
|
|
|
|||
|
|
|
|
|
|
|
|
t |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
t2 −t1 |
|
|
|
|
||
|
|
|
|
|
|
|
(A + Bt |
2 |
+Ct3 )−(A + Bt |
+Ct3 ) |
|
|
||||||
|
|
υ |
ñð |
= |
|
|
|
|
|
2 |
1 |
1 |
|
= |
|
|||
|
|
|
|
|
|
|
|
t2 −t1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
B(t |
|
|
|
|
)+(Ct3 |
−t3 ) |
|
−1)+ |
0,25(63 −13 ) |
|
|||||||
= |
2 |
−t |
= |
2,5(6 |
= |
|||||||||||||
|
|
|
1 |
|
2 |
|
|
1 |
|
|
6 |
−1 |
|
|||||
|
|
|
|
|
t2 −t1 |
|
|
|
|
|
|
|
|
|||||
= 13,25 (м/с).
Ответ: υñð = 13,25 м/с
34
Задача 2 (уровень 1)
Определить путь, пройденный телом за 10 с, если тело движется по прямолинейной траектории и его скорость изменяется по закону: υ = 30 + 2t .
Дано:
υ = 30 + 2t t = 10 c
S — ?
Решение:
Используем формулу для вычисления пути, пройденного материальной точкой за конкретное время, если известна зависимость скорости от времени:
S = t |
υ(t)dt = |
10(30 +2t)dt = (30t +t2 ) |
− |
|
∫ |
|
∫ |
10 |
|
t0 |
|
0 |
|
|
−(30t + t2 )0 = 400 м.
Ответ: S = 400 м.
Задача 3 (уровень 1)
Радиус-вектор материальной точки изменятся с течением времени по закону rr = t3ir + 3t2 rj . Определить для момента времени t = 1 c модуль скорости.
Дано:
rr = t3ir + 3t2 rj t = 1 c
υr — ?
Решение:
Используем выражения для радиус-вектора и скорости в общем виде:
rr = xi + yj + zk ,
υr = dxdt ir + dydt rj + dzdt kr.
Сравнивая выражения в общем виде с данными в задаче, получим:
x = t3, y = 3t2 ,
υx = dxdt = ddt (t3 ) = 3t2 ,
υy = dydt = ddt (3t2 ) = 6t .
Вектор скорости будет записан в следующем виде:
υr = 3t2i + 6tj .
Модуль вектора скорости:
35
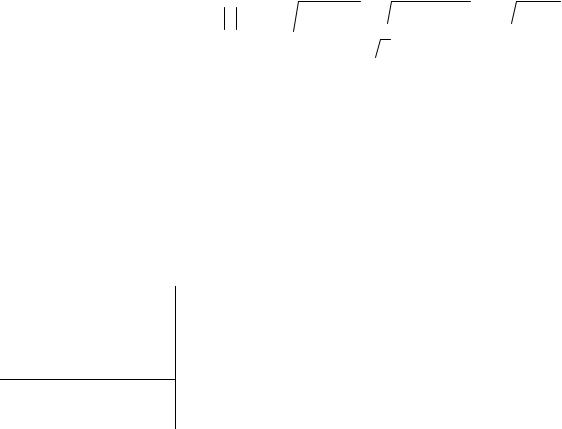
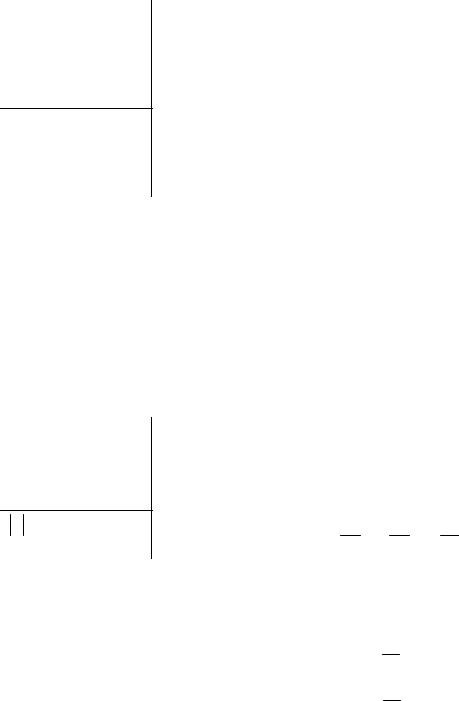
υr = υ = 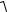 υ2x + υ2y =
υ2x + υ2y =  9t4 + 36t2 = 3t
9t4 + 36t2 = 3t t2 + 4 ,
t2 + 4 ,
υt=1 = 3 5 = 6,7 (м/с).
5 = 6,7 (м/с).
Ответ: υ = 6,7 м/с
Задача 4 (уровень 2)
Скорость материальной точки, движущейся в плоскости XY, изменяется с течением времени по закону: υr = (1−0,5t)i + 4 j . В момент времени t = 0 x = y = 0 . Записать зависимость радиуса-вектора точки от времени.
Дано: |
r |
r |
r |
||
υ = (1 |
−0,5t)i |
+ 4 j |
t = 0 с
x = y = 0 rr(t) — ?
Решение: Из определения скорости:
υr = dxdt ir + dydt rj = υxir +υy rj .
Отсюда:
dx = υxdt , |
x |
|
t |
|
∫dx |
= x − x0 |
= ∫ |
υx dt , |
|
|
x0 |
|
t0 |
|
t |
t |
|
|
|
x = x0 + ∫υxdt = ∫(1 −0,5t)dt = t −0,25t2 . |
||||
t0 |
0 |
|
|
|
Аналогично:
t t
y = y0 + ∫υy dt = ∫4dt = 4t .
t0 0
Выражение для радиуса-вектора материальной точки имеет следующий вид:
rr(t) = (t − 0,25t2 )i + 4tj .
Ответ: rr(t) = t(1 −0,25t)i + 4tj .
Аудиторные задачи
1 (1 уровень). Две материальные точки движутся в одной системе отсчета согласно уравнениям:
36

x1= 20 + 4t − 4,5t2 , x2 = 2 + 2t + 0,5t2 .
В какой момент времени скорости этих точек будут одинаковыми? Определить их скорости в этот момент времени. [0,2 с; 2,2 м/с.]
2 (2 уровень). Два тела начинают двигаться из начала системы координат. Векторы их скоростей изменяются с течением времени по законам:
υr1 = 9t2i − j + 2k ,
υr2 = 2ti + 6t2k .
Определить расстояние между телами в момент времени t = 2 с. [23,4 м.]
4.2.1.3 Ускорение материальной точки
Примеры решения задач
Задача 1 (уровень 1)
Зависимость координаты тела x от времени описывается уравнением
x = 6 −3t + 2t2 + t3 . Написать выражение зависимости ускорения тела от времени и определить среднее ускорение за время от t1 = 1 с до t2 = 4 c.
Дано:
x = 6 −3t +2t2 +t3 t1 = 1 с
t2 = 4 с
a(t) — ? аср — ?
Решение:
Определим зависимость a(t) . Для этого используем определение ускорения:
r |
|
r |
|
r |
|
dυ |
|
d 2r |
|
a |
= |
dt |
= |
dt2 . |
В нашем случае
a =a x = d 22x . dt
υx = dxdt = ddt (6 − 3t + 2t2 + t3 ) = −3 + 4t + 3t2 . ax = dtd (−3 + 4t + 3t2 ) = 4 + 6t ,
ar = (4 +6t)i .
37

Среднее ускорение тела:
|
|
r |
|
|
(−3 +4t2 +3t22 ) −(−3 +4t1 +3t12 ) |
|
||
аср= |
|
υ |
|
= |
= |
|||
|
||||||||
|
t |
|
||||||
|
|
|
|
t |
2 |
−t |
|
|
|
|
|
|
|
|
1 |
|
|
= (−3 +4 ×4 +3×42 ) −(−3 +4 +3) =19 (м/c2). 4 −1
Ответ: ar = (4 +6t)i ; aср=19 м/с2.
Задача 2 (уровень 2)
Тело брошено под углом α0 к горизонту с начальной скоростью υ0 . Определить: 1) нормальное an (t) ускорение; 2) тангенциальное aτ(t) уско-
рение в момент времени t от начала движения; 3) радиус кривизны траектории R(t).
Дано: |
|
Решение: |
α0,υ0 |
Тело, брошенное под углом к горизонту, совершает кри- |
|
an (t) — ? |
||
aτ(t) — ? |
волинейное движение в плоскости XY с постоянным уско- |
|
R(t) — ? |
рением свободного падения g , направленным вертикаль- |
|
|
но вниз. Вдоль оси x движение равномерное с постоянной |
|
|
скоростью υx = υ0 cosα0 ; вдоль оси y движение равнопе- |
|
|
ременное со скоростью |
υy = υ0 sin α0 − gt (без учета со- |
|
противления воздуха). |
|
|
Абсолютное значение скорости в любой момент времени: |
|
|
υ(t) = υ2x + υ2y = |
υ02 cos2 α0 + (υ0 sin α0 − gt)2 = |
|
= υ02 − 2gtυ0 sin α0 + g 2t2 . |
|
38
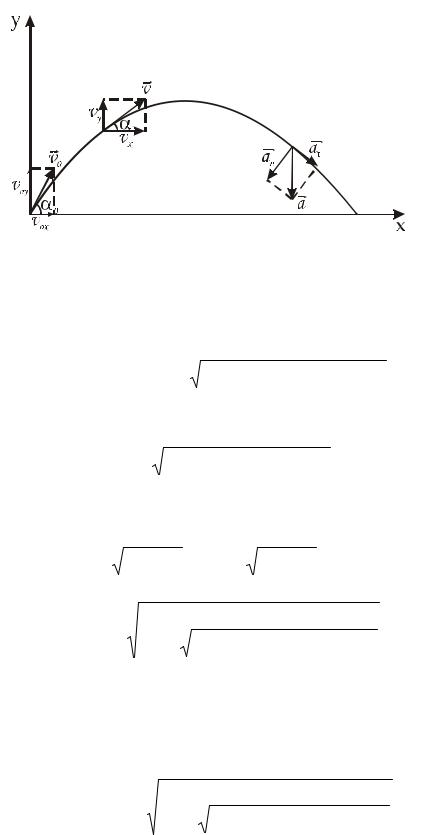
Рис. 1.9
1. Определим зависимость тангенциального ускорения от времени:
aτ(t) = |
dυ |
= |
d |
υ02 − 2gtυ0 sin α0 + g2t2 |
= |
|||
dt |
dt |
|||||||
|
|
|
|
|
|
|||
|
|
|
|
g(gt − υ0 sin α0 ) |
|
|||
= |
|
|
. |
|
||||
|
υ02 − 2gt sin α0 + g 2t2 |
|
||||||
2. Определим зависимость нормального ускорения от времени:
a = aτ2 + an2 , |
an = a2 −aτ2 , |
a = g . |
||
an = g 2 − |
|
g(gt − υ0 sin α0 ) |
|
. |
|
|
|
||
|
|
υ02 − 2gtυ0 sin α0 + g 2t2 |
||
3. Зависимость радиуса кривизны траектории от времени получим из формулы:
υ2 |
|
|
|
υ02 −2gtυ0 sin α0 + g2t2 |
|
|
|
R = an |
= |
|
|
|
|
|
. |
g |
2 |
− |
g(gt −υ0 sin α0 ) |
|
|||
|
|
|
υ02 −2gtυ0 sin α0 + g2t2 |
|
|
||
39

Аудиторные задачи
1 (уровень 1). Движение материальной точки в плоскости XY описывается законом x = At, y = At(1+Bt), где A и B — положительные постоянные. Определить ускорение точки в зависимости от времени. [a = 2AB = const.]
2 (уровень 2). Камень брошен горизонтально со скоростью υx = 15 м/с. Най-
ти нормальное и тангенциальное ускорения камня через одну секунду после начала движения.
|
υ |
x = |
gυ |
x |
|
|
|
2 |
|
υy |
|
|
g2t |
|
|
|
2 |
|
|
an = g |
|
|
|
|
|
|
=8,2 ì ñ ; |
aτ = g |
|
= |
|
|
|
|
|
= 5,4 ì ñ |
. |
||
|
2 |
|
|
2 |
|
2 |
υ |
|
|
2 |
|
2 |
|||||||
|
υ |
+ g |
t |
|
|
2 |
+ g |
t |
|
|
|||||||||
|
|
|
υx |
|
|
|
|
|
|
υx |
|
|
|
|
|||||
4.2.1.4 Кинематика вращательного движения
Примеры решения задач
Задача 1 (уровень 1)
Тело вращается вокруг неподвижной оси по закону ϕ = A + Bt +Ct2 , где
А = 10 рад, В = 20 рад, С = –2 рад/с2. Определить полное ускорение точки, которая находится на расстоянии R = 0,1 м от оси вращения, для момента времени t = 4 с.
Дано:
ϕ= A + Bt +Ct2
А= 10 рад
В = 20 рад С = –2 рад/с2
R = 0,1 м t = 4 с
a — ?
Рис. 1.10
Решение:
Полное ускорение точки, которая движется по криволинейной траектории, определяется как геометрическая сумма тангенциального ускорения aτ, направленного по
касательной к траектории, и нормального ускорения an , направленного к центру траектории:
a = aτ + an , a2 = aτ2 + an2 .
Модули тангенциального и нормального ускорений можно записать в следующем виде:
aτ =βR , an = ω2R .
Следовательно,
a =  β2R2 + R2ω4 = R
β2R2 + R2ω4 = R β2 +ω4 .
β2 +ω4 .
Угловую скорость ω найдем как первую производную угла поворота по времени:
40

ω= ddϕt = B +2Ct ,
ω = 20+2×(–2) ×4 = 4 (рад/с)
Угловое ускорение β найдем как первую производную от угловой скорости по времени:
β = ddωt = 2C = −4 (рад/с2).
Следовательно,
a = 0,1 (−4)2 + 44 =1,65 (м/c2).
(−4)2 + 44 =1,65 (м/c2).
Ответ: а = 1,65 м/с2.
Задача 2 (уровень 2)
Колесо, вращаясь равноускоренно, достигло угловой скорости ω = 20 рад/с через 10 оборотов после начала вращения. Определить угловое ускорение колеса.
Дано:
ω = 20 рад/с N = 10 об
β — ?
Решение:
При равноускоренном вращении β = ddtω = const , и тогда в результате интегрирования по времени получим:
ω= ω0 +βt = ddtϕ .
Вычисляя интеграл по времени от последнего равенства, получаем зависимость от времени угла поворота:
ϕ = ϕ0 + ω0t + βt2 . 2
По условию задачи: ϕ0 = 0,ω0 = 0 . |
|
|
|
||||
Тогда имеем: |
βt2 |
|
|
|
|
|
|
ϕ = |
, |
ω=βt, |
t = |
ω |
. |
||
2 |
β |
||||||
|
|
|
|
|
|||
С другой стороны, ϕ = 2πN .
Сравнивая написанные выше равенства, получим:
41
|
|
|
βω2 |
|
|
откуда следует, что |
2β2 = 2πN , |
|
|||
|
|
|
|||
|
ω2 |
400 |
|
2 |
|
β = |
|
= |
|
= 3,2 |
(рад/с ). |
4πN |
4 ×3,14 ×10 |
||||
Ответ: β = 3,2 рад/с2.
Аудиторные задачи
1 (уровень 1). Определить угловую скорость и угловое ускорение твердого тела, которое вращается вокруг неподвижной оси Z по закону
ϕ = at −bt2 , где a = 20 c-1, b = 1 с-2. Охарактеризовать движение этого тела. [ωz = 2(10 – t) c-1; β = –2 c-2. Тело вращается равнозамедленно и в момент времени t = 10 c останавливается, а затем направление движения изменяется на противоположное.]
2 (уровень 2). Определить угловое ускорение колеса, частота вращения которого за двадцать полных оборотов возросла от n0 = 1 об/с до n = 5 об/с.
β = π(n2 −n02 ) |
= 3,8 c−2. |
|
|
N |
|
|
|
|
4.3 МАТЕРИАЛЫ К ЛАБОРАТОРНЫМ ЗАНЯТИЯМ
4.3.1 Лабораторная работа «Изучение кинематических величин и связи между ними
при поступательном и вращательном движениях твердого тела» Основные понятия, определения и формулы кинематики
Простейшей формой движения материи является механическое движение, изучаемое в механике. Механическое движение — это перемещение
тел или частей тел друг относительно друга.
Кинематика — раздел механики, в котором изучается механическое движение без учета причин, обуславливающих это движение.
Механическая система — совокупность тел, выделенных для рассмотрения их движения. Простейшей механической системой является материальная точка.
Материальная точка — тело, размерами которого можно пренебречь при рассмотрении его движения в условиях данной задачи.
42

Для описания механической системы выбирается система отсчета. Система отсчета — это совокупность тела отсчета, т.е. тела, относительно которого рассматривается движение механической системы, неподвижно связанной с телом отсчета системы координат и часов с указанием момента начала отсчета времени.
Траектория материальной точки — это линия, которую она описы-
вает при своем движении в пространстве.
Радиус-вектор материальной точки r — это вектор, проведенный из начала выбранной системы координат в ту точку на траектории, в которой в данный момент времени находится материальная точка. Радиус-вектор материальной точки является функцией времени: r = r(t) .
Мгновенная скорость (или скорость) материальной точки — вектор-
ная величина, равная первой производной радиус-вектора материальной точ-
ки по времени: |
|
|
|||
r dr |
′ |
|
|||
|
|
|
|
||
υ = dt , или υ = r |
. |
||||
|
|||||
Вектор мгновенной скорости направлен по касательной к траектории материальной точки в сторону ее движения. Величина скорости
υ = dSdt ,
где S — пройденный путь.
Мгновенное ускорение (или ускорение) материальной точки — век-
торная величина, равная первой производной ее скорости по времени:
ar = ddtυ , или a = υ′,
или второй производной радиуса-вектора материальной точки по времени:
r |
d 2rr |
′′ |
|
|
a = |
dt2 , или a = r |
. |
||
|
При криволинейном движении материальной точки (в том числе при движении по окружности) ее ускорение можно представить в виде векторной суммы тангенциального и нормального ускорений:
ar = aτ + an , a =  aτ2 + an2 .
aτ2 + an2 .
Тангенциальное ускорение учитывает изменение величины скорости и направлено по касательной к траектории движения по направлению скорости
вслучае ускоренного движения (рис. 1.11) и против направления скорости —
вслучае замедленного движения (рис.1.12):
43
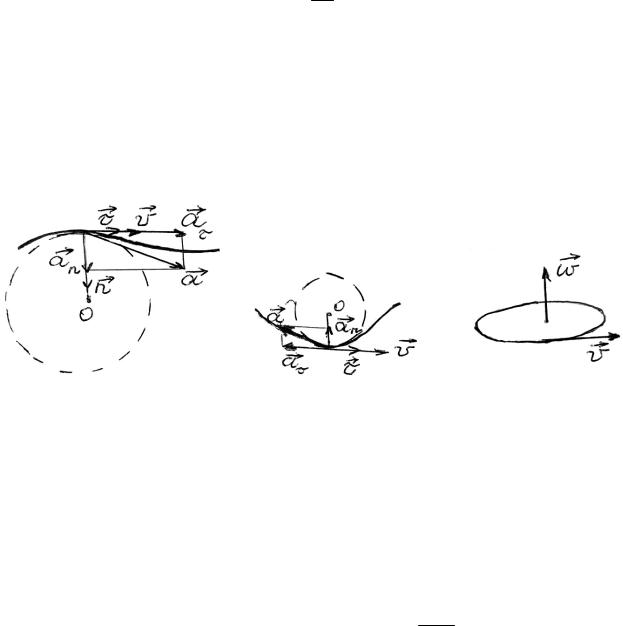
arτ = ddtυ rτ.
Нормальное ускорение учитывает изменение направления скорости материальной точки и направлено перпендикулярно траектории в сторону ее центра кривизны:
arn = υR2 nr.
Рис. 1.11 |
Рис. 1.12 |
Рис. 1.13 |
При движении с постоянным ускорением ( a = const) можно получить:
υ = υr0 + art , rr = rr0 + υr0t + art2 , 2
откуда следуют формулы для проекций векторов υ и r на ось Х:
υx = υ0x + axt , x = x0 + υ0xt + ax2t2 .
Абсолютно твердое (твердое) тело — тело, расстояние между любы-
ми двумя точками которого неизменно.
Поступательное движение твердого тела — такое его движение, при котором любая прямая, связанная с ним, остается параллельной самой себе. При поступательном движении твердого тела все его точки в каждый данный момент времени имеют одинаковые скорости и одинаковые ускорения.
При вращении твердого тела вокруг неподвижной оси его точки движутся по окружностям, расположенным в перпендикулярных к оси вращения плоскостях; центры окружностей лежат на этой оси.
44
Величина мгновенной угловой скорости вращения (угловой скоро-
сти) твердого тела вокруг неподвижной оси, а значит и движения любой его точки по окружности, есть первая производная угла поворота по времени:
ω= ddtϕ , или ω= ϕ′.
Направлен вектор угловой скорости по оси вращения в сторону, определяемую по правилу правого винта относительно направления вращения
(рис.1.13).
Мгновенное угловое ускорение (угловое ускорение) вращающегося вокруг неподвижной оси твердого тела или материальной точки, движущейся по окружности, есть первая производная угловой скорости по времени:
βr = ddtω , или β = ωr′.
При вращении твердого тела вокруг неподвижной оси все точки тела в каждый момент времени имеют одинаковые угловые скорости и одинаковые угловые ускорения. r
Для вращения с постоянным угловым ускорением (β = const) получим
векторное равенство:
ωr = ωr0 +βt ,
спроектировав которое на ось вращения Z, будем иметь:
ωZ = ω0Z +βZ t , ϕ = ϕ0 +ω0Z t + βZ2t2 .
При вращении твердого тела вокруг неподвижной оси выполняются следующие соотношения между линейной скоростью υ, тангенциальным ускорением arτ, нормальным ускорением an данной точки тела, радиусом-
вектором, проведенным из центра окружности вращения в эту точку, угловой скоростью и угловым ускорением твердого тела:
r |
υ = ωr , т.к. ω r . |
υ = ω×r , |
|
arτ =β×rr, |
aτ =βr , т.к. β rr. |
arn = −ω2rr, |
an = ω2r . |
45

Описание лабораторной установки и хода выполнения лабораторной работы
3
Рис.1.14
Пусть к концам нити, перекинутой через блок, подвешены два груза различной массы (рис. 1.14). Если к системе, состоящей из грузов 1, 2 и блока, предоставить возможность двигаться, то опытным путем можно убедиться в том, что грузы будут двигаться поступательно с постоянным ускорением, а блок будет вращаться с постоянным угловым ускорением. Для описания движения груза 1 выберем систему отсчета. Пусть закрепленная на стенде линейка будет телом отсчета, начало координат (точку О) выберем в точке начального положения груза 1 ( y0 = 0),
ось Y направим вертикально вниз. В данном случае достаточно одной оси координат, так как движение груза прямолинейное.
Вкачестве часов будем использовать секундомер, который включается
вмомент t = 0 начала движения груза 1 (следовательно, υ0 = 0). Если рас-
стояние, пройденное грузом до приемного столика 3 обозначить h , то по формулам для равноускоренного движения можно записать:
h = |
at2 |
, |
(1) |
|
2 |
||||
|
|
|
||
υ = at , |
|
(2) |
||
где υ — проекция вектора скорости груза 1 на ось Y в момент достижения им столика, a — проекция ускорения груза на эту ось.
Из выражения (1) получаем:
a = |
2h |
, |
(3) |
||
t2 |
|||||
и, подставив (3) в (2), |
|
|
|
||
2h |
|
|
|||
υ = |
. |
(4) |
|||
|
|||||
|
t |
|
|
|
|
Очевидно, что тангенциальное ускорение aτ точек, лежащих на краю
блока, равно ускорению a груза 1. Поэтому, используя связь между тангенциальным и угловым ускорением, можем найти угловое ускорение, с которым вращается блок:
β = Ra
или с учетом выражения (3):
β = |
2h |
, |
(5) |
|
t2R |
||||
|
|
|
где R — радиус блока.
46
Далее, используя выражения для угла поворота при равноускоренном вращении, можно найти угол, на который повернется блок:
ϕ = βt2 , 2
и угловую скорость его вращения в момент достижения грузом 1 приемного столика:
ω=βt ;
сучетом (5) последние выражения принимают вид:
ϕ = |
h |
|
, |
(6) |
|
R |
|||||
|
|
|
|||
ω= |
2h |
. |
(7) |
||
tR |
|||||
|
|
|
|||
Число оборотов N блока за время t можно найти из следующего выражения:
N = ϕπ .
Подставив в последнее равенство выражение (6), получаем
N = |
h |
. |
(8) |
|
|||
|
2πR |
|
|
Задания
Iуровень
1.Для двух заданных преподавателем значений h ( h1 и h2 ) произвести по
5измерений времени движения груза 1 (t1 и t2 ).
2.Измерить радиус блока R.
3.Результаты измерений занести в табл. 1.1.
4.Рассчитать средние значения t1ñð и t2ñð . Полученные значения занести в
табл. 1.2.
5. По полученным средним значениям t1ñð и t2ñð , используя формулы (3)−(5), (7), (8), вычислить значения a, υ, β, ω, N для каждого из значений h1 и h2 . Результаты вычислений занести в табл. 1.1.
47
|
|
|
|
|
|
|
|
|
|
Таблица 1.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
R = |
|
|
h1 = |
|
|
h2 = |
|||||
№ опыта, t1 |
a1 |
υ1 |
β1 |
ω1 |
N1 |
t2 |
a2 |
υ2 |
β2 |
ω2 |
N2 |
1. |
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|
4. |
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
|
|
|
|
Среднее |
|
|
|
|
|
|
|
|
|
|
|
значение |
|
|
|
|
|
|
|
|
|
|
|
IIуровень
1.Используя данные табл. 1.1, произвести необходимые расчеты и заполнить табл. 1.2.
2.Объяснить (письменно или устно по указанию преподавателя) связь между численными значениями величин, приведенных в табл. 1.2.
3.Рассчитать погрешности для одной из величин t1, t2 . При расчетах исполь-
зовать данные табл. 1.1.
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
a1 |
|
|
υ1 |
|
β1 |
|
ω1 |
|
|
N1 |
|
|
t2 |
|
|
a2 |
|
|
υ2 |
|
β2 |
|
ω2 |
|
|
N2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IIIуровень
1.По данным табл. 1.1 найти величину полного ускорения произвольной точки на ободе блока в момент времени t1 или t2 . Для выбранного момента
времени вычислить также угол между векторами скорости и ускорения точки на ободе блока.
2. Пусть ускорение груза 1 не постоянно, а зависит от времени по линейному закону a = bt , где b = const . Каким в этом случае будет время прохождения грузом пути h1 (или h2 )?
48
4.3.2Контрольные задания к лабораторной работе
4.3.2.1Вопросы предварительного контроля
(компьютерный допуск к лабораторной работе)
Скорость материальной точки. Путь, пройденный материальной точкой
1.Первую половину пути автомобиль двигался со скоростью 40 км/ч, а вторую — 60 км/ч. С какой средней скоростью двигался автомобиль?
2.Мгновенная скорость материальной точки — это
1)производная пути по времени;
2)отношение пути к промежутку времени движения;
3)производная радиуса-вектора материальной точки по времени;
4)интеграл от пути по времени.
3.Какое из написанных ниже выражений правильно определяет вектор скорости?
1) |
dS |
; |
2) |
S |
; |
3) |
r(t |
|
− t |
) ; |
||
|
dt |
|
|
t |
|
|
|
|
2 |
1 |
|
|
4) |
drr |
; |
5) |
|
|
S |
; 6) |
|
dυ |
. |
|
|
dt |
t |
2 |
−t |
dt |
|
|
||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
4.Материальная точка движется в плоскости XY так, что ее координаты зависят от времени следующим образом:
x = 3t + 2t2 , y = 5.
Найти величину скорости материальной точки в момент времени 1 с.
5. Радиус-вектор материальной точки, движущейся в плоскости XY , изменяется с течением времени по закону:
rr = 3ti + 2t2 j .
Найти величину скорости материальной точки в момент времени 1 с.
6.Величина вектора скорости материальной точки, движущейся в пространстве, зависит от времени по закону:
υ= 6t м/с.
Какой путь прошла материальная точка за первые 2 с движения?
7.Величина вектора скорости материальной точки, движущейся по окружности, зависит от времени по закону:
υ= (3 +6t) м/с.
49
Какой путь прошла материальная точка за первые 2 с движения?
Ускорение материальной точки
1.Мгновенное ускорение материальной точки (ускорение) — это
1)производная радиуса-вектора материальной точки по времени;
2)производная пути по времени;
3)отношение скорости ко времени;
4)производная скорости по времени.
2.Материальная точка движется в плоскости XY так, что ее координаты зависят от времени по законам:
x = 2t +5t2 , y = 3.
Найти нормальное ускорение материальной точки в момент времени 1 с. 3. Какое из написанных ниже выражений определяет вектор ускорения?
1) |
dS |
|
; |
4) |
|
dr |
; |
|
||
dt |
|
|
dt |
|
||||||
|
|
|
|
|
|
|
|
|||
2) |
υ |
; |
|
5) |
dυ |
|
|
|
|
|
t |
|
dt |
|
dυ |
|
|||||
|
|
|
|
|
|
|||||
|
r |
|
|
|
|
|
|
|
|
|
3) υ(t2 |
−t1 ) ; |
|
6) |
|
|
|
. |
|||
|
|
|
dt |
|||||||
|
|
|
|
|
|
|
|
|
|
|
4.Материальная точка движется по окружности радиуса 6 м со скоростью, величина которой зависит от времени по закону:
υ = 2t .
Найти нормальное и тангенциальное ускорение материальной точки в момент времени 3 с.
5.Материальная точка равномерно движется по окружности радиуса 2 м со скоростью 6 м/c. Чему равны тангенциальное, нормальное и полное ускорение материальной точки?
6.Небольшое тело брошено вертикально вверх. Какие составляющие вектора ускорения имеет тело во время движения?
1)Тангенциальное ускорение;
2)нормальное ускорение;
3)тангенциальное и нормальное ускорения.
7.Небольшое тело брошено в горизонтальном направлении. Какие составляющие вектора ускорения имеет тело во время движения?
1)Тангенциальное ускорение;
2)нормальное ускорение;
3)тангенциальное и нормальное ускорения.
50
Угловая скорость и угловое ускорение
1.Тело вращается вокруг неподвижной оси так, что угол поворота зависит от времени по закону:
ϕ= 2t2 + 3t .
Вычислить величину угловой скорости для момента времени 1 с.
2.Тело вращается вокруг неподвижной оси так, что угол поворота зависит от времени по закону:
ϕ= 4sin t + 2t .
Чему равна величина угловой скорости тела в момент времени t = 0.
3.Материальная точка движется по окружности. Как направлен вектор угловой скорости материальной точки?
1)Вдоль радиуса окружности от ее центра;
2)по касательной к окружности;
3)вдоль радиуса окружности к ее центру;
4)перпендикулярно окружности вверх;
5)перпендикулярно окружности по правилу правого винта относительно вращения.
4.Материальная точка движется по окружности радиуса R так, что угол поворота зависит от времени по закону:
ϕ = At2 + Bt .
Как зависит величина линейной скорости материальной точки от времени?
5.Материальная точка движется по окружности с угловой скоростью, зависящей от времени по закону:
ω= 5t .
Как направлен вектор углового ускорения?
1)Вдоль радиуса окружности;
2)также как вектор угловой скорости;
3)по касательной к окружности;
4)перпендикулярно окружности по правилу правого винта относительно вращения;
5)перпендикулярно окружности вниз.
6.Угловое ускорение материальной точки при ее движении по окружности — это
1)производная радиуса-вектора материальной точки по времени;
2)производная пути по времени;
3)производная скорости по времени;
51
4)производная угловой скорости по времени;
5)отношение угловой скорости ко времени.
7.Линейная скорость материальной точки, движущейся по окружности радиуса 3 м, меняется по закону:
υ= 6t2 .
Вычислить угловое ускорение материальной точки в момент времени 1 с.
Вопросы по выполнению лабораторной работы
1. Какие из приведенных ниже величин измеряются в данной лабораторной работе?
1) |
a ; |
4) S; |
7) R; |
2) |
υ; |
5) h1 ; |
8) T; |
3) t1 ; |
6) t2 ; |
9) N. |
|
2.Какие из приведенных ниже величин вычисляются в данной лабораторной работе?
1) t1 ; |
4) h1 ; |
7) υ1; |
2) a ; |
5) h2 ; |
8) T; |
3) t2 ; |
6) N1 ; |
9) υ2 . |
3.Нить с привязанными к ее концам грузами перекинута через блок. За время t каждый груз проходит расстояние h , начиная свое движение из положе-
ния равновесия. По какой формуле можно вычислить скорость грузов в последний момент движения?
4.Нить с привязанными к ее концам грузами перекинута через блок. Первый раз грузы проходят расстояние h1 за время t1 , второй раз — расстояние h2
за время t2 . Величина ускорения грузов в первом опыте a1 , во втором — a2 . Какое соотношение справедливо для величин этих ускорений?
1) a1 > a2 ; 2) a1 = a2 ; 3) a1 < a2 .
5.Пусть за время 2 с грузы, привязанные к нити, перекинутой через блок, прошли расстояние 0,5 м. Зная, что радиус блока равен 0,1 м, вычислить угловую скорость в последний момент времени движения грузов.
6.Грузы в лабораторной установке первый раз двигались 2 с, второй раз — 1 с. Во втором случае блоком был сделан 1 оборот. Сколько оборотов сделал блок в первом опыте?
52
4.3.2.2 Контрольные вопросы для защиты лабораторной работы
Iуровень
1.Дать определение кинематических величин: (мгновенной) скорости, (мгновенного) ускорения, тангенциального и нормального ускорений, угловой скорости и углового ускорения.
2.Найти связь между линейной скоростью и угловой скоростью точки, движущейся по окружности.
3.Записать для равнопеременного (равноускоренного и равнозамедленного) движения выражения, определяющие скорость и пройденный путь в зависимости от времени.
4.Знать рабочие формулы, по которым в данной лабораторной работе вычисляются линейное ускорение грузов, угловое ускорение точек блока, линейная и угловая скорости точек блока в момент приземления груза, число оборотов блока за время движения блока.
5.Знать последовательность измерений и вычислений.
IIуровень
1.Исходя из общих выражений, определяющих вектор (мгновенной) скорости, вектор (мгновенного) ускорения, получить выражения для координаты движущейся точки (груза) и проекции ее скорости на некоторую ось при равноускоренном движении.
2.Исходя из общего выражения для пути, пройденного материальной точкой (поступательно движущимся телом), вывести формулу пути для равноускоренного движения.
3.Получить рабочие формулы (3), (4), (5), (6), (7).
4.Проанализировать отношения, записанные в табл. 2. Какие из них теоретически должны быть равны 1? Какие из них должны совпадать?
IIIуровень
1.Проанализировать движение точки обода вращающегося блока: найти зависимость тангенциального, нормального и полного ускорений указанной точки от времени. Определить также зависимость от времени угла между скоростью и ускорением указанной точки.
2.Пусть грузы в лабораторной установке движутся с ускорением, которое зависит от времени по закону: a = bt , где b = const . Найти время t1 , которое
потребуется грузам в таком случае, чтобы пройти выбранное расстояние h1 .
53
4.4 МАТЕРИАЛЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
Задание № 1
Получить формулу для вычисления пути, пройденного материальной точкой, при заданной зависимости величины скорости от времени (см. п. 3.2.1.2 «Скорость материальной точки»).
Задание № 2
Применить полученное общее выражение к случаю равнопеременного движения с начальной скоростью.
Задание № 3
Выполнить индивидуальное задание по решению следующих задач на тему «Кинематика материальной точки и вращательного движения абсолютно твердого тела».
1 Радиус-вектор. Путь. Вектор перемещения. Уравнение траектории
Уровень 1
1.1.Определить, какой путь пройдет тело за время 10 с от начала движения, если зависимость координаты от времени при его движении имеет вид:
x = 2t2 + 3t + 4 . [230 м.]
1.2. Зависимость пути от времени описывается уравнением: S = At2 − Bt2 +Ct3 , где А = 2 м/с, В = 3 м/с2 и С = 4 м/с3. Определить расстояние, которое прошло тело за 2 с после начала движения. [24 м.]
1.3. Материальная точка движется в плоскости XY по закону: õ = At, y = Bt , x = At, y = Bt , где А и В — положительные постоянные величины. Напи-
сать уравнение траектории. Построить ее график. |
|
AB |
y = |
. |
|
|
|
x |
1.4.Радиус-вектор частицы задается выражением: rr = 3ti + 4tj +7kr. Опреде-
лить перемещение частицыr заr первые 10 с движения и модуль этого пе-
ремещения. [ rr = 300i + 400 j ; 500 м.]
1.5.Радиус-вектор материальной точки относительно начала системыr rкоординат изменяется с течением времени по закону: rr = Ati + Btj , где
А = 4 м/с, В = 5 м/с. Написать уравнение траектории. [y = 2,5 x.]
x.]
54

Уровень 2
1.6. Тело брошено под углом α0 к горизонту с начальной скоростьюυ0 . Оп-
ределить уравнение траектории тела. |
y = x tg α |
0 |
− |
g |
x2. |
|
|||||
|
|
|
2υ02 cos2 α0 |
|
|
|
|
|
|
|
1.7. Из трех труб, расположенных на земле, с одинаковой скоростью бьют струи воды под углами α1 = 60º, α2 = 45º; α3 = 30º к горизонту. Пренеб-
регая сопротивлением воздуха, найти: 1) отношение L1/L2/L3 дальностей падения воды на землю; 2) отношение Н1/Н2/Н3 максимальных высот подъема этих струй. [L1/L2/L3 =  3 / 2 /
3 / 2 /  3 ; Н1/Н2/Н3 = 3/2/1.]
3 ; Н1/Н2/Н3 = 3/2/1.]
1.8.Движение материальной точки в плоскости описывается уравнениями:
x= Acosωt, y = Asinωt , где A и B — постоянные величины. Определить
уравнение траектории точки. |
x2 |
+ |
y2 |
=1. |
|||
|
|
2 |
|
||||
|
|
B |
2 |
|
|||
|
A |
|
|
|
|
||
1.9.Две материальные точки начинают двигаться из начала системы коорди-
нат в одной и той же системе отсчета. Радиусы-векторы точек изменяются по законам: rr1= t2ir −2t3k , rr2 =1,5t3i −2t2 j +t2k . Определить расстояние между точками через 1,5 с после начала движения. [323,3 м.]
1.10.Два тела одновременно начинают двигаться вдоль оси X так, что их ра-
диусы-векторы изменяются с течением времени по законам: rr1 = 2t2i , rr2 = (20 −3t)i . Определить радиус-вектор r точки встречи тел.
[rr =12,5i .]
2 Вектор скорости материальной точки
Уровень 1
2.1.Определить среднюю скорость движения автомобиля, если известно, что 1/4 часть времени он двигался со скоростью 16 м/с, а оставшееся время — со скоростью 8 м/с. [10 м/с.]
2.2.Радиус-вектор материальной точки относительно начала системы координат изменяется с течением времени по закону: r = Atir − Bt2 j , гдеr
А = 2 м/с, В = 6 м/с. Определить: а) проекции скорости на оси координат; б) зависимость от времени вектора скорости и его модуль в момент вре-
|
|
r |
|
−12tj ; 24,1 м/с.] |
|
|
|
мени t =2 с. [ υ = 2i |
|
|
|||||
2.3. |
Прямолинейное |
движение |
точки |
описывается |
уравнением: |
||
rr = 3t2ir |
+ 4t2 rj +8tkr |
. Определить зависимость вектора скорости от вре- |
|||||
мени и путь, |
пройденный |
точкой |
за первые 4 |
с движения. |
|||
r |
r |
r |
; 8 м.] |
|
|
|
|
[ υ = 6ti |
+8tj +8k |
|
|
|
|||
55

2.4. Движение тела задается уравнением: x = At + Bt2 +Ct3 , где A = 5 м/с, B = 0,2 м/с2, C = 0,1 м/с2. Определить скорость материальной точки в моменты времени t1 = 2 с и t2 = 4 с, а также среднюю скорость за промежу-
ток времени от t1 до t2 . [7 м/с; 11,4 м/с; 9 м/с.]
2.5. Зависимость пройденного телом пути от времени описывается уравнением: S = 6 −3t +2t2 +t3 . Определить в интервале времени от t1 = 1 с до t2 = 4 с среднюю скорость тела. [28 м/с.]
2.6.Тело движется в плоскости XY по закону: x = At, y = Bt , где A и B — по-
ложительные величины. Определить величину скорости υ в зависимости от времени. Написать уравнение траектории.
|
1 |
2 |
4 |
|
2 |
|
AB |
|
υ = |
|
|
A t |
|
+ B |
|
; y = |
. |
t |
2 |
|
|
|||||
|
|
|
|
|
|
|
x |
|
Уровень 2
2.7.С башни высотой h = 40 м брошено тело со скоростью υ0 = 20 м/с под углом α = 45º к горизонту. Пренебрегая сопротивлением воздуха, определить скорость падения тела на землю. [34,4 м/с.]
2.8.За время прямолинейного движения τ (0 ≤ τ ≤ t ) скорость тела описывалась уравнением: υ = At + Bt +Ct2 . Определить среднюю скорость тела
за промежуток времени τ. |
υср= A + |
Bτ + Cτ2 |
. |
|
|
|
2 |
3 |
|
|
|
|
||
2.9.Скорость материальной точки, движущейся в плоскости XY изменяется с течением времени по закону: υr = Ai −2Btj , где A и B — положительные постоянные величины. Определить зависимость от времени модуля скорости точки и ее радиуса-вектора r , если в начальный момент времени он был равен 0. [ υ =  A2 +4B2t2 , rr = Ati − B2tj .]
A2 +4B2t2 , rr = Ati − B2tj .]
2.10.Зависимость пройденного телом пути от времени задается уравнением:
S = A + Bt +Ct2 , где A = 3 м; B = 2 м/с; C = 1 м/с2. Определить среднюю скорость тела за вторую секунду его движения. [υ = 5 м/с.]
3 Ускорение материальной точки
Уровень 1
3.1.Движение точки задается уравнениями: x = 8t2 + 4 , y = 6t +3, z = 0 . Оп-
ределить модуль скорости и ускорения точки в момент времени 10 с. [200 м/с; 40 м/с2.]
56

3.2. Зависимость координаты тела от времени задается уравнением: x = A + Bt +Ct2 + Dt4 , где C = 0,1 м/с2, D = 0,03 м/с3. Через какое время после начала движения ускорение будет равно 2 м/с2? Найти среднее ускорение тела за этот промежуток времени. [10 c; 1,1 м/с2.]
3.3. Кинематические уравнения движения двух материальных точек имеют
вид: |
x |
= A t + B t2 |
+C t3 |
, |
x |
2 |
= A t + B t2 |
+C |
t3 , где B1 = 4 м/с2, |
||
|
1 |
1 |
1 |
1 |
|
|
2 |
2 |
2 |
|
|
C1 = −3 м/с3; B2 = −2 м/с2; C2 = 1 м/с3. В какой момент времени ускорения этих двух точек будут одинаковыми? [0,5 с.]
3.4. Радиус-вектор материальной точки относительно начала координат изменяется со временем по закону: rr = 2t2i −5t2 j . Найти уравнение траек-
тории, зависимость от времени ускорения и его модуль в момент време-
ни t1 = 0,2 c. [y = −2,5x; ar = 4i −10 j ; 10,8 м/с2.]
3.5.Тело движется равноускоренно с начальной скоростью υ0 . Определить
ускорение тела, если за время t = 2 c оно прошло путь S = 16 м и его скорость стала υ = 3υ0 . [4 м/с2.]
Уровень 2
3.6.Материальная точка движется вдоль прямой так, что ее ускорение линейно растет и за первые 10 с достигает значения 5 м/с2. Определить в конце десятой секунды скорость точки и пройденный точкой путь, если начальная скорость равна нулю. [25 м/с; 83,3 м.]
3.7.С вершины горы брошено тело в горизонтальном направлении со скоростью 19,6 м/с. Определить тангенциальное и нормальное ускорения тела через 2 с после начала движения. Какой угол образует вектор полного ускорения с вектором скорости? Сопротивление воздуха не учитывать. [ aτ = g2t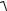 υ02 + g2t2 =6,9 м/с2; an = υ0 g
υ02 + g2t2 =6,9 м/с2; an = υ0 g υ02 + g2t2 =1,9 м/с2; 45°.]
υ02 + g2t2 =1,9 м/с2; 45°.]
3.8.Тело брошено горизонтально со скоростью υ0 = 15 м/с. Не учитывая сопротивление воздуха, определить радиус кривизны траектории тела через 2 с после начала движения. [102 м.]
3.9.Тело движется прямолинейно. Ускорение этого тела задается законом:
a = 2t + 2t2 . Определить скорость тела через 2,5 с после начала движения из состояния покоя. Какой путь оно пройдет за это время? [6,67 м/с; 4,43 м.]
3.10.Тело 1 движется равноускоренно, имея начальную скорость υ10 = 2 м/с
иускорение a. Через время 10 c после начала движения тела 1 из этой же
точки начинает двигаться равноускоренно тело 2, имея начальную скорость υ20 = 12 м/с и то же ускорение a. При каком ускорении тело 2
сможет догнать тело 1? [a > 1 м/с2.]
57
4 Кинематика вращательного движения
Уровень 1
4.1.Линейная скорость υ1 точки, находящейся на ободе вращающегося диска, в три раза больше, чем линейная скорость υ2 точки, находящейся на 6 см ближе к его оси. Определить радиус диска. [9 см.]
4.2.Диск вращается вокруг неподвижной оси так, что зависимость угла по-
ворота радиуса диска от времени задается уравнением: ϕ = At2 , где
А = 0,1 рад/с2. Определить полное ускорение а точки на ободе диска к концу второй секунды после начала движения, если линейная скорость этой точки в этот момент υ = 0,4 м/с. [0,26 м/с2.]
4.3. Материальная точка вращается по окружности R = 0,2 м с постоянным угловым ускорением β = 1,5 рад/с2. Определить в момент времени t = 0,5 с его полное ускорение a, нормальное ускорение an , тангенциальное ускорение aτ, угловую скорость ω, линейную скорость υ. [0,32 м/с2; 0,11 м/с2; 0,3 м/с2; 0,75 рад/с; 0,15 м/с.].
4.4.Якорь электродвигателя, имеющий частоту вращения n = 50 с-1, после
выключения тока, сделав N = 628 оборотов, остановился. Определить угловое ускорение якоря. [12,5 рад/с2.]
4.5.Колесо автомашины вращается равнозамедленно. За время 2 мин оно изменило частоту вращения с 240 до 60 мин-1. Определить: 1) угловое ус-
корение колеса; 2) число полных оборотов, сделанных колесом за это время. [0,157 рад/с2; 300.]
Уровень 2
4.6.На вал радиусом R = 10 см намотана нитка, к концу которой привязан груз. Двигаясь равноускоренно, груз за τ = 20 с от начала движения опустился на h = 2 м. Определить угловую скорость и угловое ускорение вала для этого момента времени.
ω= 2h |
= 2 ðàä/ñ; |
β = |
|
2h |
= 0,1 ðàä/ñ2 |
. |
|
|
|
||||||
|
Rτ |
|
|
(Rτ)2 |
|
||
|
|
|
|
||||
4.7. Зависимость углового |
ускорения от |
времени задается уравнением: |
|||||
β = 5At3 + 12Bt2 (A = 3 рад/с5; B = 1,3 рад/с4). Какой угловой скорости достигнет материальная точка через 2 с после начала движения из состояния покоя? Чему равно ее угловое перемещение за это время? [18,4 рад/с; 3,2 рад.]
4.8. Ось с двумя дисками, которые находятся на расстоянии 0,5 м друг от друга, вращается с частотой n = 1600 об/мин. Пуля, летящая вдоль оси, пробивает оба диска. При этом отверстие в первом диске смещено относительно отверстия во втором диске на угол ϕ = 12º. Определить скорость пули. [400 м/с.]
58

4.9.Точка движется по окружности радиусом R = 15 см с постоянным тангенциальным ускорением aτ. К концу четвертого оборота после начала
движения линейная скорость точки υ = 15 см/с. Определить нормальное ускорение an точки через 16 c после начала движения. [1,5 см/с2.]
4.10.Колесо вращается с угловым ускорением β = 2 рад/c2. Через время 0,5 с после начала движения линейное ускорение точки колеса стало равно
|
|
a |
|
|
|
|
a = 13,6 см/с2. Найти радиус колеса. R = |
|
|
|
|
= 6,1 ì. |
|
|
|
2 |
|
4 |
||
|
β |
1+β |
t |
|
||
|
|
|
|
Уровень 3
4.11. Лодка пересекает реку с постоянной относительно воды, перпендикулярной к берегам скоростью υ = 0,3 м/с. Ширина реки b = 63 м. Скорость течения изменяется по параболическому закону:
|
|
u |
0 |
|
b |
2 |
|
u = u0 |
− 4 |
|
x − |
|
, |
||
b |
2 |
||||||
|
|
|
2 |
|
где x — расстояние от берега, u0 — константа, равная 5 м/с. Найти снос
лодки s вниз по течению от пункта ее отправления до места причала на противоположном берегу реки. [700 м.]
4.12. Колесо радиусом R равномерно катится по горизонтальной поверхности. От точки А (рис. 1.15) отрывается капелька грязи. С какой скоростью движется колесо, если, побывав в воздухе, капля снова опустилась в ту же точку колеса при том же его положении? Сопротивление воздуха
не учитывать. [ υ =n Rgπ, |
где n — число оборотов колеса.] |
||
А |
А |
||
|
|
|
|
|
|
Рис. 1.15 |
|
5 ОБРАЗЕЦ КОНТРОЛЬНЫХ ЗАДАНИЙ
Iуровень (репродуктивный)
1.Что принимается за материальную точку?
2.Что такое радиус-вектор материальной точки и вектор перемещения?
3.Дать определение вектору мгновенной скорости материальной точки.
4.Привести формулу для вычисления пути, пройденного материальной точкой при произвольном ее движении.
5.Что такое среднее ускорение материальной точки за определенный промежуток времени?
59
6.Что определяет тангенциальное ускорение? Записать его в векторном виде.
7.Что такое радиус кривизны траектории в данной точке?
8.Чему равна величина и каково направление вектора угловой скорости вращения твердого тела вокруг неподвижной оси?
9.Задача.
Камень, брошенный горизонтально, через время 0,5 с после начала движения имел скорость в 1,5 раз большую скорости в момент бросания.
Скакой скоростью был брошен камень?
IIуровень (продуктивный)
1.Разложить вектор мгновенного ускорения на нормальную и тангенциальную составляющие. Получить окончательные выражения для нормальной
итангенциальной составляющей в векторном виде.
2.Найти связь между линейной и угловой скоростями точки, движущейся по окружности (в векторном виде).
III уровень (творческий)
Рассмотреть движение точки обруча радиуса R, катящегося без скольжения по горизонтальной плоскости со скоростью υ. Записать кинематические уравнения движения точки (зависимость координат от времени), найти выражения для скорости, ускорения, радиуса кривизны траектории, угла между векторами скорости и ускорения в зависимости от времени.
60
МОДУЛЬ 2
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА.
РАБОТА И МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
Комплексная цель. Студент должен:
а) знать (описывать и формулировать) понятия и определения массы, си-
лы, импульса, импульса силы, центра масс системы материальных точек, механической работы, мощности, кинетической энергии, консервативной силы, потенциальной энергии, полной механической энергии; законы Ньютона, движения центра масс, изменения импульса, сохранения импульса, сохранения механической энергии, изменения механической энергии, теорему о кинетической энергии;
б) доказывать (получать) и характеризовать законы изменения импульса, cохранения импульса, движения центра масс, изменения механической энергии, сохранения механической энергии; выражение для работы переменной силы; консервативность сил гравитации, сил тяжести и сил упругости, связь между потенциальной энергией и консервативной силой;
в) моделировать и прогнозировать движение системы материальных точек или поступательное движение тел на основе законов движения и законов сохранения;
г) уметь
–собирать и анализировать незнакомую информацию, путем логического мышления приходить к выводу,
–применять полученные теоретические сведения к решению задач поступательного движения тел,
–проверять экспериментом законы динамики.
Преподаватель должен формировать социально-личностные качества студента: умение изучать собственные сильные и слабые стороны, реально оценивать свои силы.
1 ВВЕДЕНИЕ. БАЗОВЫЕ ПРОБЛЕМЫ МОДУЛЯ
Динамика материальной точки и поступательного движения твер-
дого тела. Первый закон Ньютона. Инерциальные системы отсчета. Сила. Масса. Второй закон Ньютона. Третий закон Ньютона. Импульс. Основной закон динамики материальной точки. Основной закон поступательного движения твердого тела (системы материальных точек). Понятие замкнутой механической системы. Законы изменения и сохранения импульса. Центр масс системы материальных точек и закон его движения.
Работа и механическая энергия. Механическая работа. Работа переменной силы. Мощность. Кинетическая энергия. Теорема о кинетической
61
энергии материальной точки и системы материальных точек. Силовое поле. Понятие центрального поля сил. Понятие однородного поля сил. Консервативные и неконсервативные силы. Консервативность сил тяжести, упругости и тяготения. Потенциальная энергия материальной точки во внешнем силовом поле. Связь консервативной силы с потенциальной энергией. Понятие потенциальной энергии взаимодействия. Закон изменения полной механической энергии системы. Закон сохранения механической энергии.
Дополнительный материал. Применение законов сохранения импульса и механической энергии к абсолютно упругому и абсолютно неупругому ударам.
2 УЧЕБНО-ИНФОРМАЦИОННАЯ МОДЕЛЬ МОДУЛЯ
№, тема занятия |
Тип занятия |
Вид занятия |
Кол-во часов |
||
|
|
|
|
|
на 1 занятие |
Занятие 1 |
|
|
|
||
Динамика материальной точ- |
Знакомство |
Лекция |
2 |
||
ки и поступательного движе- |
с новым материалом |
|
|
||
ния твердого тела |
|
|
|
|
|
|
|
|
|
||
Занятие 2 |
|
|
|
||
Работа. Механическая энер- |
Углубление |
Лекция |
2 |
||
гия |
|
|
|
|
|
|
|
|
|
||
Занятие 3 |
|
|
|
||
Законы динамики |
поступа- |
Углубление, |
Практическое |
2 |
|
тельного движения |
|
обобщение |
занятие |
|
|
|
|
|
|
||
Занятие 4 |
|
|
|
||
Работа. Механическая энер- |
Углубление, |
Практическое |
2 |
||
гия |
|
|
обобщение. |
занятие |
|
|
|
|
Текущий контроль |
|
|
Занятие 5 |
|
|
|
||
Определение |
коэффициента |
Систематизация, |
Лабораторное |
1 |
|
трения при скольжении тела |
обобщение. Предва- |
занятие |
|
||
по наклонной плоскости |
рительный контроль |
|
|
||
|
|
|
|
||
Занятие 6 |
|
|
|
||
Применение законов сохра- |
Систематизация, |
Управляемая само- |
2 |
||
нения импульса и механиче- |
обобщение |
стоятельная работа |
|
||
ской энергии |
к |
абсолютно |
|
студентов |
|
упругому и абсолютно неуп- |
|
|
|
||
ругому ударам |
|
|
|
|
|
|
|
|
|
||
Занятие 7 |
|
|
|
||
Динамика материальной точ- |
Суммарный |
|
1 |
||
ки и поступательного движе- |
контроль |
|
|
||
ния твердого тела. Работа и |
|
|
|
||
механическая энергия |
|
|
|
||
62
3НАУЧНО-ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
3.1СЛОВАРЬ ПОНЯТИЙ
3.1.1Новые понятия
1.Инертностью материальной точки (или тела) называется способность сохранять состояние покоя или равномерного прямолинейного движения.
2.Масса материальной точки (тела) есть мера инертности.
3.Система отсчета называется инерциальной, если по отношению к ней выполняется первый закон Ньютона: материальная точка (тело) находится в состоянии покоя или равномерного прямолинейного движения, если на нее не действуют другие тела или их действие скомпенсировано.
4.Второй закон Ньютона: ускорение материальной точки или поступательно движущегося тела равно отношению векторной суммы сил, действующих на материальную точку (тело), к ее массе.
5.Третий закон Ньютона утверждает, что силы взаимодействия между любыми двумя материальными точками равны по величине, противоположны по направлению и направлены вдоль прямой, соединяющей эти точки.
6.Импульс материальной точки есть произведение ее массы на вектор скорости.
7.Импульс силы, действующей на материальную точку, есть произведе-
ние вектора силы на промежуток времени ее действия.
8.Центром масс системы материальных точек называется точка, радиус-
вектор которой есть отношение векторной суммы произведений масс точек системы на их радиусы-векторы к массе всей системы.
9.Внутренними силами системы материальных точек называются силы взаимодействия между точками этой системы. Внешними силами системы называются силы, с которыми на точки системы действуют материальные точки (тела), не входящие в данную систему.
10.Импульсом системы материальных точек (поступательно движущих-
ся тел) называется векторная сумма импульсов всех точек (тел), входящих в данную систему.
11.Система материальных точек (поступательно движущихся тел) называется замкнутой (изолированной), если на нее не действуют внешние силы.
12.Элементарная механическая работа есть произведение модуля силы на величину элементарного перемещения и на косинус угла между направлениями силы и перемещения.
13.Средняя мощность за некоторый промежуток времени есть отноше-
ние работы, выполненной за этот промежуток времени, к величине этого промежутка.
63
14.Кинетическая энергия материальной точки (поступательно движу-
щегося твердого тела) есть половина произведения массы точки (тела) на квадрат ее скорости.
15.Сила, действующая на материальную точку, называется консервативной, если работа этой силы при перемещении материальной точки из точки 1 в точку 2 траектории не зависит от формы траектории, соединяющей точки 1 и 2, а зависит только от их положения в пространстве.
16.Потенциальная энергия материальной точки, находящейся под дейст-
вием консервативных сил (в поле консервативных сил) — это такая скалярная функция положения материальной точки, изменение которой с противоположным знаком (убыль) при перемещении материальной точки из точки 1 в точку 2 равно работе консервативных сил, совершаемой по любой траектории, соединяющей точки 1 и 2.
17.Градиентом скалярной функции (например, потенциальной энергии)
называется вектор, компоненты которого по осям декартовой прямоугольной системы координат равны соответствующим частным производным скалярной функции. Консервативная сила, действующая на материальную точку, является градиентом потенциальной энергии материальной точки с противоположным знаком.
18.Полной механической энергией системы материальных точек (по-
ступательно движущихся тел) называется алгебраическая сумма кинетических энергий всех материальных точек (тел) системы, потенциальных энергий взаимодействия материальных точек между собой и потенциальных энергий материальных точек системы во внешнем консервативном силовом поле.
3.1.2Понятия для повторения
1.Материальная точка.
2.Вектор (мгновенной) скорости материальной точки.
3.Траектория движения материальной точки.
4.Вектор (мгновенного) ускорения материальной точки.
5.Система отсчета.
6.Вектор перемещения.
3.2ОСНОВНОЙ ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
3.2.1Динамика материальной точки и поступательного движения
твердого тела
3.2.1.1Законы динамики материальной точки
Воснове классической (ньютоновой) механики лежат три закона Ньютона, сформулированные в 1687 году. Эти законы явились обобщением мно-
64

гочисленных экспериментов и теоретических исследований, проведенных Ньютоном и его предшественниками.
Первый закон Ньютона
Для материальной точки он формулируется следующим образом: суще-
ствуют такие системы отсчета, относительно которых материальная точка сохраняет состояние покоя или равномерного прямолинейного движения, если на нее не действуют другие тела или их действия взаимно компенсируются.
Свойство материальных точек (или тел) сохранять состояние покоя или прямолинейного равномерного движения называется инертностью. Первый закон Ньютона носит название закона инерции, а движение тела при отсутствии на него воздействий или при их компенсации — движением по инерции.
Системы отсчета, относительно которых выполняется закон инерции, называются инерциальными системами отсчета. Опыты свидетельствуют, что с большой точностью инерциальной системой отсчета можно считать гелиоцентрическую систему отсчета, связанную с центром масс Солнечной системы. Экспериментально установлено, что если есть одна инерциальная система отсчета, то любая другая, движущаяся относительно нее равномерно и прямолинейно или покоящаяся, тоже является инерциальной (см. также модуль3, п. 3.3.1.1 «Силы инерции при поступательном движении неинерциальной системы отсчёта»). Система отсчета, связанная с Землей, строго говоря, не является инерциальной, в основном из-за суточного вращения Земли вокруг собственной оси. Но, учитывая то, что это вращение очень медленное (1 оборот за 24 часа), при решении множества задач систему отсчета, связанную с Землей, часто считают инерциальной.
Второй закон Ньютона
Механическое взаимодействие между материальными точками (телами) может осуществляться при непосредственном соприкосновении точек или тел (например, при ударе тел, давлении одного на другое), а также на расстоянии, когда тела не соприкасаются. В последнем случае считается, что взаимодействие осуществляется через силовое поле. Силовое поле — это особая форма материи, передающая действие одних тел (материальных точек) на другие. В каждом случае для описания механического действия тел
одного на другое вводится векторная физическая величина — сила. Сила F полностью задана, если указаны ее модуль F = F , направление и точка при-
ложения. Прямая линия, вдоль которой направлена сила, называется линией действия силы. Опытыr показывают, что в инерциальной системе rотсчета под
действием силы F материальная точка изменяет свою скорость υ, приобретает ускорение a , которое пропорционально величине (модулю) силы и на-
65

правлено как вектор силы. Это утверждение можно записать в следующем виде:
ar = kF . |
(2.1) |
Величина коэффициента пропорциональности k определяется инертностью материальной точки, т.к. этот коэффициент устанавливает связь между силой, действующей на материальную точку, и ускорением, с которым она откликается на действие силы. В качестве меры инертности в механике принята положительная скалярная величина m — масса материальной точки или тела. Чем большая инертность материальной точки и вместе с тем ее масса, тем меньшее ускорение она приобретает под действием определенной силы
Fr . Поэтому k = m1 , и (2.1) приобретает вид:
r |
F |
|
a |
= m . |
(2.2) |
Для сравнения масс m1 и m2 двух материальных точек достаточно сравнить ускорения a1 и a2 , приобретаемые этими материальными точками под действием определенной силы. r
Если на материальную точку действует N сил: F1, F2 , ... , FN , то каждая
из них вызывает у материальной точки такое же ускорение, как и в случае действия только одной этой силы. Это утверждение следует из опытов и называется принципом независимости действия сил. С учетом этого ускорение a , приобретаемое материальнойr точкой массой m под действием одновре-
менно приложенных к ней сил F1, F2 , ... , FN , запишется в следующем виде:
r |
N |
r |
N |
F |
|
1 |
N |
r |
a |
= ∑ai = ∑ |
i |
= |
|
∑F . |
|||
|
||||||||
|
i=1 |
|
i=1 m |
|
m i=1 |
|
||
Измерения показывают, что одновременное действие сил Fri (i =1,..., N ) ,
приложенных в одной точке, полностью эквивалентно действию силы F , равной их векторной сумме:
Fr |
N |
|
= ∑Fri , |
(2.3) |
|
|
i=1 |
|
в том смысле, что сила Fr rвызывает то же самое механическое действие, что совместное действие сил Fi . Сила F называется равнодействующей или ре-
зультирующей. С учетом обозначения (2.3) предыдущее выражение для ускорения материальной точки приобретает вид, аналогичный (2.2):
r |
|
1 N |
F |
|
|
|
a |
= |
|
i∑=1Fi = m |
, |
(2.4) |
|
m |
||||||
66
Формула (2.4) выражает второй закон Ньютона для материальной точ-
ки: ускорение материальной точки равно отношению векторной суммы сил, действующих на материальную точку, к ее массе. Этот закон выполняется только по отношению к инерциальным системам отсчета.
Третий закон Ньютона
Наблюдения и опыты показывают, что механическое действие двух тел одного на другое всегда являются их взаимодействием: если тело 2 действует на тело 1, то обязательно тело 1 в то же время действует на тело 2. Количественное описание механического взаимодействия тел дается в третьем законе Ньютона, который для двух материальных точек формулируется следующим образом: две материальные точки взаимодействуют между собой с силами, одинаковыми по величине и направленными в противоположные стороны вдоль соединяющей эти точки прямой, т.е.
F21 = −F12 , |
(2.5) |
где Fr21 — сила, с которой на материальную точку с номером 2 действует материальная точка с номером 1, F12 — соответственно сила, с которой мате-
риальная точка 2 действует на точку 1. Третий закон Ньютона выполняется только в инерциальных системах отсчета.
Второй закон Ньютона (2.4) является основным законом классической механики материальной точки, т.к. он дает возможность решить основную задачу механики — определить траекторию материальной точки и ее скорость в каждый момент времени, если известна масса материальной точки, силы, действующие на нее, и так называемые начальные условия, т.е. координаты и скорость материальной точки в начальный момент времени. Запишем второй закон Ньютона в другом виде. Введем понятие импульса материальной точки. Импульс материальной точки — это вектор, равный произведению массы материальной точки на вектор ее скорости:
p = mυ. |
(2.6) |
Учитывая определение вектора ускорения (1.21), второй закон Ньютона (2.4) можно записать в виде:
m dυ = ∑N Fri . dt i=1
В классической механике считается, что масса материальной точки (тела) не зависит от ее скорости и, значит, от времени. (Не будем рассматривать
67
здесь движение тел с переменной по смыслу задачи массой.) На этом основании величину m в предыдущем равенстве можно внести под знак производной, что, с учетом (2.6), приведет к следующему уравнению:
r |
N |
|
= Fr . |
(2.7) |
dp |
= ∑Fr |
|||
dt |
i=1 |
i |
|
|
В таком виде основной закон динамики материальной точки означает: производная импульса материальной точки по времени равна результирующей всех сил, приложенных к ней.
Если обе части равенства (2.7) умножить на dt, получится:
dpr |
N |
|
= ∑Fidt = Frdt . |
(2.8) |
|
|
i=1 |
|
Векторная величина Fridt называется импульсом силы Fi за элементар-
ный промежуток времени dt. Изменение импульса материальной точки за конечный промежуток времени от момента t1 до момента t2 получим в результате вычисления определенного интеграла от выражения (2.8):
pr |
t |
t |
|
2 − pr1 = ∫2 dpr |
= ∫2 Frdt . |
(2.9) |
|
|
t1 |
t1 |
|
Соотношение (2.9) означает, что изменение импульса материальной точки за промежуток времени t = t2 −t1 равно импульсу результирующей силы, при-
ложенной к материальной точке за этот промежуток времени.
3.2.1.2 Закон изменения импульса механической системы. Закон сохранения импульса
Рассмотрим произвольную систему N материальных точек. Силы, действующие на материальные точки системы, это внутренние и внешние силы. Внутренние силы — это силы взаимодействия между любыми двумя точками системы. Например, на материальную точку с номером 1 действуют внутренние силы (рис. 2.1): f12 — со стороны материальной точки с номером 2,
f13 — со стороны точки с номером 3 и т.д. В общем виде: на точку с номе-
ром i действуют внутренние силы fik , где k = 1, 2,…, N, кроме k = i. Вместе с
тем, на каждую материальную точку системы действуют силы со стороны материальных точек или тел, не входящих в выделенную систему материальных точек. Это внешние силы. Обозначим результирующую всех внешних
68

сил, действующих на материальную точку с номером 1, соответственно F1 , на точку с номером 2 — Fr2 и т.д. Запишем уравнение второго закона Ньюто-
на в виде (2.7) для материальной точки системы, имеющей номер i = 1, выделяя внутренние и внешние силы:
dpr |
= |
r |
|
|
r |
+... |
|
r |
r |
N |
r |
r |
||
1 |
f |
|
+ f |
|
+ f |
+ F |
= ∑ f |
+ F . |
||||||
dt |
|
12 |
|
|
13 |
|
|
|
1N |
1 |
k =1 |
1k |
1 |
|
Для i-ой материальной точки соответственно |
|
|
|
|||||||||||
|
|
|
|
r |
|
|
N |
|
|
+ Fr . |
|
|
(2.10) |
|
|
|
|
dpi |
= ∑ fr |
|
|
|
|||||||
|
|
|
|
dt |
|
|
k =1 |
ik |
i |
|
|
|
|
|
Если сложить уравнения типа (2.10), написанные для всех материальных точек, т.е. для всех i = 1, 2,…, N, получим
N |
r |
N N |
|
N |
|
(2.11) |
∑dpi = ∑ ∑ fr |
+ ∑Fr. |
|||||
i=1 |
dt |
i=1k =1 |
ik |
i=1 |
i |
|
Поменяем местами в левой части последнего уравнения знак суммы и знак производной. Тогда получим левую часть (2.11) в виде:
|
N |
dpr |
|
d |
N r |
|
dP |
|
|
|
∑ |
i |
= |
|
∑ p |
= |
dt |
, |
(2.12) |
|
|
||||||||
где Pr |
i=1 |
dt |
|
dt i=1 i |
|
|
|
||
— векторная величина, равная векторной сумме импульсов всех мате- |
|||||||||
риальных точек, входящих в систему: |
|
|
N r |
|
|||||
|
r |
r |
|
r |
|
|
r |
(2.13) |
|
|
P = p1 |
+ p2 +... + pN |
= ∑ pi , |
||||||
|
|
|
|
|
|
|
|
i=1 |
|
называется импульсом системы материальных точек.
Двойная сумма внутренних сил в правой части равенства (2.11) на основании третьего закона Ньютона равна нулю. Действительно,
N N |
r |
r |
r |
r |
r |
|
∑ ∑ fik = |
f12 |
+ f13 |
+... + fik + fki +... = 0, |
(2.14) |
||
i=1k =1 |
|
|
|
|
|
|
т.к. эта сумма содержит каждые две силы взаимодействия между каждыми двумя материальными точками системы. С учетом (2.5) это ведет к (2.14).
Подставив (2.12) и (2.14) в (2.11), получим дифференциальное уравнение:
dP = ∑Fr |
= F âíåø |
, |
(2.15) |
|
N |
|
|
|
|
dt i=1 |
i |
|
|
|
которое выражает закон изменения импульса механической системы:
производная импульса системы материальных точек по времени равна векторной сумме всех внешних сил, действующих на систему. Иногда вектор-
69
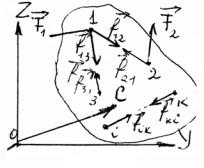
ную сумму внешних сил называют главным вектором внешних сил. Он обозначен в (2.15) Frâíåø .
Применим закон изменения импульса системы материальных точек (2.15) к случаю замкнутой системы. Замкнутой (изолированной) системой материальных точек называется такая система, на которую не действуют внешние силы или они взаимно компенсируются. В этом случае из (2.15)
вытекает: |
|
|
|
|
dPr |
=0. |
(2.16) |
|
dt |
||
|
|
|
|
Равенство (2.16) означает, что вектор импульса системы материальных точек с течением времени не изменяется:
Pr = const. |
(2.17) |
Таким образом, приходим к закону сохранения импульса системы мате-
риальных точек: импульс замкнутой системы материальных точек с течением времени остается постоянным.
3.2.3 Центр инерции системы материальных точек и закон его движения. Основной закон динамики поступательного движения абсолютно твердого тела
Пусть дана произвольная система N материальных точек, движение которых рассматривается в определенной инерциальной системе отсчета (рис. 2,1). Центром инерции (центром масс) системы материальных точек называется точка С, радиус-вектор которой определяется следующим выражением:
|
|
r |
|
r |
r |
|
N |
r |
|
|
|
|
|
|
∑m r |
|
|||||
rr |
= |
m1r1 |
+m2 r2 |
+... +mN rN |
= |
i=1 |
i i |
. |
(2.18) |
|
|
|
|
N |
|
||||||
c |
|
m1 |
+m2 |
+... +mN |
|
|
|
|
||
|
|
|
∑mi |
|
||||||
|
|
|
|
|
|
|
i=1 |
|
|
|
Сумма, записанная в знаменателе выражения (2.18), представляет собой массу системы. Исходя из (2.18), определим скорость центра инерции системы материальной точки. С этой целью вычислим производную по времени отмеченного выражения:
Рис. 2,1
70

r |
|
|
r |
m |
r |
r |
|
+... +m |
|
r |
|
|
|
|
dr |
υ +m |
υ |
2 |
N |
υ |
N |
||||
υ |
ñ |
= c = |
1 |
1 2 |
|
|
|
|||||
|
|
dt |
|
|
m1 +m2 +... +mN |
|
|
|||||
|
|
|
|
|
|
|||||||
∑N mi υri
= i=1N . (2.19)
∑mi
i=1
На основании (2.13) выражение, стоящее в числителе дроби (2.19), является
импульсом системы материальных точек P . Учитывая это и обозначая массу системы
N
∑mi = m, (2.20)
i=1
получим
r |
(2.21) |
P = mυc . |
Равенство (2.21) утверждает, что импульс системы материальных точек равен произведению массы системы на скорость ее центра инерции (центра масс). Подставляя (2.21) в закон изменения импульса механической системы (2.15),
получим закон движения центра инерции системы материальных точек
постоянной массы в следующем виде:
d (mυ |
c |
) |
|
dυ |
c |
r |
|
|
|
= m |
|
= Fâíåø , |
(2.22) |
||
dt |
|
|
dt |
||||
|
|
|
|
|
|||
который звучит следующим образом: центр масс системы материальных точек движется как материальная точка, масса которой равна массе системы, на которую действует сила, равная векторной сумме всех внешних сил, приложенных к системе (результирующая внешних сил, или главный вектор внешних сил).
Таким образом, изменить скорость центра масс системы можно только действием внешних сил. При их отсутствии центр инерции (масс) системы движется с постоянной по величине и направлению скоростью (или покоится, когда эта скорость равна нулю).
Если система представляет собой твердое тело, движущееся поступательно, то в каждый момент времени скорость всех точек системы одинаковая, υñ = υ. В этом случае, как вытекает из (2.19), скорость центра масс
|
N |
r |
|
|
r |
∑mi υi |
r |
|
|
i=1 |
|
|
||
υñ = |
|
= υ. |
(2.23) |
|
|
m |
|||
|
|
|
|
|
Подставляя (2.23) в (2.22), получим основной закон динамики поступа-
тельного движения твердого тела:
m |
dυ |
N |
r r |
внеш |
, |
(2.24) |
dt |
= ∑F = F |
|
||||
|
i=1 |
i |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
71

или в виде:
r |
|
1 |
N |
r |
|
1 |
r |
âíåø , |
|
a |
= |
|
∑F |
= |
|
F |
(2.25) |
||
|
m |
||||||||
|
|
m i=1 |
i |
|
|
|
|
||
что полностью совпадает с основным законом динамики материальной точки (2.4): ускорение поступательного движения твердого тела равно отношению
векторной суммы внешних сил, приложенных к телу, к массе тела. Силы Fi
приложены, вообще говоря, к разным точкам тела. Опыты показывают, что скорость поступательного движения тела не изменяется при параллельном переносе внешних сил в центрrмасс тела, если он является одной из точек те-
ла. На этом основании силы Fi можно считать приложенными в одной точке
тела — его центре масс, а сила Frâíåø является равнодействующей в указанном выше смысле.
Совпадение основного закона динамики для материальной точки и твердого тела, движущегося поступательно, приводит к тому, что закон сохранения импульса выполняется также для системы твердых тел, движущихся поступательно. Поэтому указанный закон обобщается следующим образом: импульс замкнутой системы материальных точек или движущихся поступательно твердых тел остается постоянным. Выполнение закона сохранения импульса является основой реактивного движения.
Если системой материальных точек является твердое тело, движущееся произвольным образом, то, зная внешние силы, с помощью соотношения
(2.22) можно найти ускорение центра масс тела ddtυc и его скорость υrñ , если она известна в начальный момент времени t = 0. Как доказывается в меха-
нике, |
скорость υi произвольной точки твердого тела в момент времени |
|
r |
r |
r r |
trυi = υA +ω× rA , где υA − скорость определенной выделенной точки тела А, ω — угловая скорость вращения тела вокруг оси, проходящей через точку А
(мгновенная ось поворота). Соответственно произвольное движение тела представляется как совокупность поступательного движения со скоростью
υrA и поворота вокруг мгновенной оси, проходящей через точку А. Учитывая то, что из (2.22) определяется скорость центра масс, в качестве его удобно выбрать точку А.
3.2.2 Работа и механическая энергия
3.2.2.1 Механическая работа. Работа переменной силы. Мощность
Пусть тело движется по определенной траектории и при этом на него действует сила F . Действие силы F на движущееся тело характеризуется
72
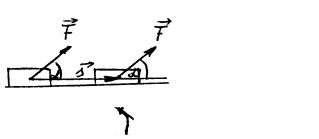
специальной физической величиной, которая называется работой силы F . Дадим сначала определение этой величины в простейшем случае.
Допустим, тело движется поступательно прямолинейно и сила F , действующая на тело в каждой точке его траектории, имеет одинаковую величину и направление во всех точках траектории. На рис. 2.2, а показано действие
на тело постоянной силы F , направленной под углом α к перемещению тела.
При этих условиях величина работы силы F при перемещении тела (центра масс тела) из точки 1 в точку 2 определяется следующей формулой:
A = FS cos α . |
Sr |
(2.26) |
Если ввести в рассмотрение вектор перемещения |
, модуль которого |
равен пути S, пройденному телом между точками 1 и 2, предыдущее выражение для работы можно будет записать в виде скалярного произведения
A12 = F S = FS S = FSF . |
(3.27) |
Два последних варианта записи |
|
в (3.27) получены с учетом свойств |
|
скалярного произведенияr: FS — это |
|
проекция вектора силы F на вектор |
|
перемещения S , FS = Fcosα; |
|
а) |
|
б) |
Рис. 2.2 r |
SF = Scosα — проекция вектора перемещения S |
|
на вектор силы |
F |
. Из определений (3.26) и (3.27) видно, что работа является |
скалярной алгебраический величиной. Для бесконечно малого (элементарного) перемещенияr тела dSr (вектор dS совпадает с обычным вектором пере-
мещения dr ) элементарная работа δA силы может быть записана в следующих различных видах:
δA = F dS = FdS cosα= FS dS = FdSF |
= |
= FX dx + Fydy + FZ dz. |
(2.28) |
|
Перейдем к определению работы силы в общем случае. Допустим, тело движется поступательно по криволинейной траектории и на него в каждой
точке траектории действует определенная сила F , величина и направление которой изменяется при переходе тела из одной точки траектории в другую.
При таких условиях говорят, что имеем случай переменной силы F (рис. 2.2, б), где показана траектория движения одной точки тела, например его центра масс). Для вычисления работы переменной силы должен быть задан закон изменения вектора силы вдоль траектории. Каждая точка траектории харак-
теризуется значением момента времени t, когда центр масс тела (или материальная точка) находится в данной точке пространства. Можно также характе-
ризовать каждую точку траектории величиной пути S, пройденного телом поступательно от начала движения. Иначе говоря, как время t, так и путь S
73
могут быть выбраны в качестве параметра траектории. На основании (2.28) для вычисления элементарной работы силы необходимо знать величину FS в
каждой точке траектории (выберем соответствующую форму записи δА в (2.28)). Пусть дан закон изменения этой величины в зависимости от изменения выбранного параметра точки на траектории, т.е. дана функция FS(S). Построим график этой функции (рис. 2.3), откладывая по горизонтальной оси
путь S, измеренныйr вдоль траектории, а по вертикальной — FS — проекцию вектора силы F в каждой точке траектории на бесконечно малое перемеще-
ние dS из этой точки в соседнюю (это бесконечно малое перемещение dS направлено по касательной к траектории). На рис. 2.3 точки 1 и 2 по оси S соответствуют точкам 1 и 2 траектории, показанной на рис. 2.2, б. Разделим отрезок 12 (рис. 2.3) на малые участки S1, S2,… Si ,…, SN и вычислим ра-
боту Ai силы на одном из них, |
Si . При этом будем считать, что величина и |
направление силы F на пути |
Si не меняется, что ведет к постоянству про- |
екции FS, которую обозначим Fsi . Выберем, например, в качестве величины Fsi на каждом отрезке Si значение функции FS (S) в начальной точке отрезка. Принятое допущение означает, что плавную линию графика зависимости
FS(S) заменяем ломаной ступенчатой линией. На участке траектории |
Si ра- |
бота силы F (из-за нашего допущения) |
|
Ai Fsi Si . |
(2.29) |
Рис. 2.3 Рис. 2.4
Величина этой работы равна площади вертикальной полоски, заштрихованной на рис. 2.3. Целиком работа А12 при перемещении тела (материальной точки) из точки 1 в точку 2 по траектории вычисляется как сумма выражений типа (2.29):
N |
N |
|
A12 = ∑ |
Ai ∑Fsi Si . |
(2.30) |
i=1 |
i=1 |
|
Очевидно, что равенство (2.30) будет тем более точным, чем на меньшие части Si разделен отрезок пути 1 — 2. Точное значение работы силы получим
74
из формулы (2.30) при переходе в ней к пределу при условии, что длина всех отрезков Si стремится к нулю (при этом количество N будет стремиться к бесконечности):
N
A12 = lim ∑Fi Si . (2.31)
S→0 i=1
Выражениеr (2.31) является определением криволинейного интеграла от функции F(S) по определенной траектории С:
A12 = ∫FS dS.
C
С учетом (2.28) подынтегральную функцию последнего выражения можно записать в других видах, например:
A12 = ∫FS dS = ∫F dS = ∫(Fidx + Fydy + Fzdz). |
(2.32) |
||
c |
C |
C |
|
Таким образом, работа переменной силы F , действующей на движущуюся материальную точку или поступательно движущееся твердое тело, вычисляется с помощью криволинейного интеграла (2.32) по траектории. Величина этого интеграла численно равна площади криволинейной трапеции под линией графика зависимости FS(S).
Для вычисления криволинейного интеграла (2.32) уравнение траектории должно быть известно. Если, например, траектория дана в параметрическом виде (1.2) с параметром t (время), то дифференциалы координат материальной точки, с помощью которых записано подынтегральное выражение в (2.32), вычисляются через производные функций (1.2):
dx = dx dt, |
dy = dy dt, |
dz = dz dt. |
dt |
dt |
dt |
В этом случае криволинейный интеграл (2.32) превращается в определенный интеграл по переменной t:
|
r |
r |
2 |
|
A12 = ∫ |
F |
dS |
= ∫(Fx xt′ + Fy yt′ + Fz zt′)dt. |
(2.33) |
C |
|
|
1 |
|
При определенных свойствах силы F вычисление работы с помощью криволинейного интеграла упрощается.
Используем общую формулу работы (2.32) для вычисления работы внешней силы, деформирующей (сжимающей или растягивающей) упругую пружину при выполнении закона Гука. Пусть длина недеформированной
пружины равна l0 (рис. 2.4, а). Будем считать, что внешняя сила F , действующая вдоль оси X, в каждый момент времени равна по величине и направ-
лена противоположно силе упругости F óïð . Тогда проекция силы F на ось X
Fx = −Fxóïð =kx,
где x — удлинение пружины, k — ее жесткость. График функции Fx (x) показан на рис. 2.4, б. Он представляет собой прямую линию, проходящую через начало координат, соответствующую растяжению пружины для x > 0 и
75

сжатию — при x < 0. Работу этой силы при растяжении от удлинения x1 до x2 можно определить, исходя из формулы (3.7), в которой FS = Fx = kx ,
Fy = Fz= 0.
12 |
|
2 |
|
kx2 |
|
kx2 |
|
= |
∫ |
kxdx = |
2 |
− |
1 . |
(2.34) |
|
A |
|
||||||
|
|
1 |
|
2 |
|
2 |
|
К такому же результату придем, вычисляя работу A12 как площадь криволинейной трапеции, ограниченной ординатами x = x1 , x = x2 и линией графи-
ка зависимости Fx ( x ). Криволинейная трапеция в данном случае представляет собой прямоугольную трапецию. При сжатии пружины от деформации x1
до x2 ( в этом случае x1 и x2 – отрицательные), придем также к результату
(2.34).
Работа, выполняемая за единицу времени, называется мощностью. Если за элементарный промежуток времени выполняется элементарная работа δA,
то мгновенная мощность
P = |
δA . |
(2.35) |
|
dt |
|
δA определяетсяr выражениями (2.28), в которых вектор элементарного пере-
мещения dS =drr = υrdt на основании (1.9). С учетом этого формула для мгновенной мощности предстанет в виде:
P = F ×υr |
(2.36) |
3.2.2.2 Кинетическая энергия механической системы. Теорема о кинетической энергии материальной точки и системы материальных точек
Энергия является универсальной мерой различных форм движения и взаимодействий. Механическая энергия — мера способности тела выполнять механическую работу. Существует механическая энергия двух видов —
кинетическая и потенциальная.
Придем к понятию кинетической энергии материальной точки следующим образом. Допустим, что на материальную точку массой m действует
ряд сил: F1, F2 ,..., FN , — и в результате этого материальная точка движется
по определенной траектории. Второй закон Ньютона, являясь основным законом динамики материальной точки, служит дифференциальным уравнением
движения этой материальной точки: |
|
|
|
|
|||
|
r |
r |
r |
r |
N |
r |
|
m |
dυ |
(2.37) |
|||||
dt |
= F |
+ F |
+... + F |
= ∑F . |
|||
|
1 |
2 |
N |
i=1 |
i |
|
|
Умножим обе части уравнения (2.37) скалярно на вектор υdt . Получим
76

r r |
r |
r |
r |
r r |
N |
r r |
(2.38) |
mυ dυ = Fi υdt + F2 |
υdt +... + FN υdt = ∑Fi υdt. |
||||||
|
|
|
|
|
i=1 |
|
|
Обратим внимание на произведение υd υ, стоящее в левой части равенства (2.38). Чтобы представить его в ином виде, напомним, что квадрат модуля
произвольногоr вектора b — это скалярное произведение вектора b на век-
тор b . Для вектора скорости материальной точки υ это запишется в следующем виде:
r r r |
(2.39) |
υ2 = υ υ = υ2 (υ≡ υ). |
Вычислим дифференциал от обеих частей равенства (2.39) (имеется в виду первое равенство). Напомним, что дифференциал определенной функции f (x) представляет собой основную линейную часть приращения этой функ-
ции при изменении аргумента:
df = dfdx dx = fx′dx.
Вычисление дифференциала функции υ2 приводит с учетом (2.39) к следующему равенству:
r r |
r r |
dυr rdυ |
r r |
|
||||
d(υ2 ) = d(υ υ) = (υ υ)′t |
dt = |
|
υ+υ |
|
dt = 2υ dυ. |
(2.40) |
||
dt |
|
|||||||
|
|
|
|
dt |
|
|
||
Разделив обе части (2.40) на 2 и внося постоянный коэффициент под знак производной, получим соотношение:
|
υ2 |
|
r r |
(2.41) |
d |
2 |
|
= υ dυ. |
|
|
|
|
|
|
|
|
|
|
|
Используем (2.41) в уравнении движения материальной точки (2.38) и заметим, что υdt согласно определению вектора скорости равен перемещению
dS . С учетом этого (2.38) принимает следующий вид:
|
υ2 |
|
r |
r |
r |
r |
r |
r |
N |
r |
r |
(2.42) |
md |
|
|
= F |
dS |
+ F |
dS |
+... + F |
dS |
= ∑F |
dS. |
||
|
2 |
|
1 |
|
2 |
|
N |
|
i |
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
В левой части (2.42) константу m можно поднести под знак дифференциала. |
|||||||||
Произведение же |
r r |
|
|
|
|
|
|
|
|
FdS представляет собой, на основании (2.28), элементар- |
|||||||||
ную работу δAi силы Fi |
при перемещении материальной точки dS . С уче- |
||||||||
том этого из (2.42) получим: |
|
|
|
|
|
||||
|
mυ2 |
|
|
|
N |
|
|||
|
d |
|
|
|
= δA |
+δA |
+... +δA |
= ∑δA . |
(2.43) |
|
|
|
|||||||
|
|
|
|
1 |
2 |
N |
1 |
|
|
|
2 |
|
|
|
|
|
i=1 |
|
|
Если вычислить определенный интеграл от обеих частей (2.43) в пределах от момента времени t1 до момента времени t2:
77
|
t2 |
|
mυ2 |
t2 |
|
1 |
+ |
t2 |
2 |
+... + |
t2 |
|
N |
|
|||||
|
∫ |
|
|
|
|
∫ |
|
∫ |
∫ |
|
|
||||||||
|
|
d |
|
= |
|
|
δA |
|
δA |
|
|
δA , |
|
||||||
|
t1 2 t1 |
|
|
|
t1 |
|
|
|
t1 |
|
|
|
|||||||
получим следующее выражение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
mυ2 |
|
mυ2 |
|
|
|
|
|
|
|
|
|
N |
|
||||||
|
|
|
|
− |
|
|
|
= A + A |
+... + A |
= ∑A . |
(2.44) |
||||||||
|
|
|
|
||||||||||||||||
|
2 |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
N |
i |
|
|||
|
|
2 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
i=1 |
|
|||
(2.44) показывает, |
что изменение величины |
mυ2 |
за промежуток времени |
||||||||||||||||
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t = t2 − t1 равно алгебраической сумме работ всех сил, приложенных к ма-
териальной точке, за этот промежуток времени. Скалярная физическая величина, равная половине произведения массы материальной точки на квадрат ее скорости, называется кинетической энергий материальной точки:
W = |
mυ2 |
|
|
|
, Wk > 0. |
(2.45) |
|
|
|||
k |
2 |
|
|
|
|
|
|
Так как уравнение движения материальной точки (2.7) и поступательного движения твердого тела (2.25) одинаковые по форме (с учетом 2.6), то равенство (2.44) справедливо также для твердого тела, движущегося поступательно. Соответственно, (2.45) означает кинетическую энергию материальной точки или поступательно движущегося твердого тела. Равенство
(2.44) называется теоремой о кинетической энергии материальной точки или тела при поступательном движении. Она звучит следующим образом:
изменение кинетической энергии материальной точки или поступательно движущегося твердого тела за промежуток времени t равно работе всех сил, приложенных к материальной точке (твердому телу) за этот промежуток времени:
N
Wk2 -Wk1 = Wk = ∑Ai = Aâñåõ . (2.46)
i=1
Кинетическая энергия есть энергия движения. Она зависит от выбора
системы отсчета, так как от этого зависит величина скорости υ. Кинетическая энергия является величиной аддитивной. Это означает,
что кинетическая энергия системы материальных точек представляет собой сумму кинетических энергий отдельных материальных точек или частей системы.
Пусть имеем систему N материальных точек, на которые действуют внутренние и внешние силы. Для каждой точки системы можно написать уравнение, аналогичное (2.46)
W |
i |
−W |
i |
= |
W |
i |
iâñåõ |
, |
(2.47) |
|
|
|
|
|
= A |
||||||
k |
2 |
k |
|
k |
|
|
|
|||
|
|
|
1 |
|
|
|
|
|
|
|
где Aiâñåõ — работа всех сил (внутренних и внешних), приложенных к материальной точке с номером i . Сложим равенства типа (2.47), относящиеся ко всем точкам системы:
78
N ∑Wki2 i=1
N |
i |
N |
iâñåõ |
. |
(2.48) |
− ∑Wk |
= ∑A |
||||
i=1 |
1 |
i=1 |
|
|
|
|
|
|
|
||
Каждая сумма кинетических энергий материальных точек, входящая в левую часть равенства (2.48), представляет собой кинетическую энергию системы в соответствующий момент времени:
N
∑Wki2 =Wk2 i=1
N
∑Wki1 =Wk1 (2.49)
i=1
Правую часть (2.48), представляющую собой работу всех сил системы (внутренних и внешних) за промежуток времени t обозначим:
N |
(2.50) |
∑Ai âñåõ = Aâñåõ. |
i=1
Спомощью обозначений (2.49) и (2.50) теорема о кинетической энергии сис-
темы материальных точек (2.48) приобретает следующий вид:
W |
|
−W = Aâñåõ = Aвнутр + Aâíåø . |
(2.51) |
k |
2 |
k |
|
|
1 |
|
Таким образом, теорема о кинетической энергии для системы материальных точек или тел, движущихся поступательно, имеет следующую формулировку: изменение кинетической энергии системы материальных точек (или тел при поступательном движении) равно работе всех сил, внутренних и внешних, действующих на все точки системы.
Обратим внимание на то, что работы внутренних сил, действующих между двумя точками системы, например, точками с номерами i и j, не компенсируют друг друга. Это происходит потому, что силы взаимодей-ствия по
третьему закону Ньютона fij = − f ji , но перемещения этих точек dS j и dSi за
определенный промежуток времени в общем случае неодина-ковые. Кинетическую энергию системы материальных точек можно предста-
вить в виде суммы кинетической энергии поступательного движения со скоростью ее центра масс и кинетической энергии движения материальных точек относительно центра масс. Для произвольного движения твердого тела такое деление означает, что кинетическая энергия твердого тела равна сумме кинетической энергии его поступательного движения со скоростью центра масс и кинетической энергии вращательного движения тела вокруг оси, проходящей через центр масс.
79

3.2.2.3 Силовое поле. Консервативные силы
Если на материальную точку, движущуюся или покоящуюся, в каждой точке пространства действует сила со стороны других тел или материальных точек, говорят, что эта материальная точка находится в силовом поле (в поле сил). Например, вблизи поверхностиr Земли на каждую материальную точку действует сила тяжести mg (m — масса материальной точки и g — уско-
рение свободного падения), поэтому говорим, что имеем поле сил тяжести и т.д.
Среди силовых полей, существующих в природе, особую группу составляют так назывемые консервативные поля, или поля консервативных сил. Одно из определений консервативных (полей) сил следующее. Пусть материальная точка находится в силовом поле так, что в каждой точке поля
на материальную точку действует сила f , являющаяся функцией координат
и времени, f (x, y, z,t) . Для некоторых силовых полей существует опреде-
ленная скалярная функция U (x,y,z,t), через которую вектор силы в каждой точке пространства выражается следующим образом:
|
|
|
|
|
r |
= |
∂U r |
+ |
∂U r |
+ |
∂U r |
(2.52) |
||||
|
|
|
|
|
f |
∂x |
i |
∂y |
j |
∂z |
k. |
|||||
∂U |
|
∂U |
|
∂U |
|
|
|
|
|
|
|
|
||||
, |
, |
− частные производные функции U (x,y,z,t); i , j,k − единич- |
||||||||||||||
∂x |
∂y |
∂z |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ные векторы вдоль осей координат. При выполнении равенства (2.52) сила f называется потенциальной, а функция U (x,y,z,t) — потенциальной функ-
цией. Если к тому же функция U не зависит явно от времени t (является функцией только координат, U (x,y,z,)), то силовое поле называется консервативным.
Кроме приведенного определения существуют другие, ему эквивалентные. Дадим еще одно, физически более понятное определение консерва-
тивности сил. Сила f (или силовое поле f ) называется консерватив-
ной, если работа силы f при перемещении материальной точки из точки 1 в
точку 2 при действии этой силы не зависит от вида траектории, соединяющей точки 1 и 2, а зависит от положения этих точек в пространстве. Приведем примеры нескольких наиболее распространенных консервативных сил. При этом будем использовать приведенное выше определение консервативности.
80
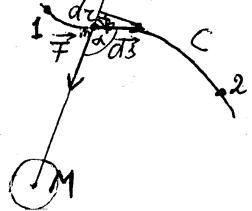
Пример 1. Покажем, что гравитационное поле консервативно. Пусть в гравитационном поле, созданном материальной точкой или однородным шаром массы М, находится материальная точка массой m (рис. 2.5 ). В соответствии с законом всемирного тяготения на массу m со стороны гравитационного по-
ля массой М действует сила всемирного
тяготения |
f , равная по величине |
Рис 2.5 |
|
f = G Mm . |
(2.53) |
r2 |
|
где r – расстояние между материальными точками с массами m и М, а в случае, когда М — масса шара, расстояние между центром шара и материаль-
ной точкой массы m; G — гравитационная постоянная, равная
6,7×10-11 Нм2/кг2.
Сила, определяемая формулой (2.53), направлена по прямой, соединяющей материальные точки с массами m и M (или m и центр шара массы М), является силой притяжения. Допустим, что на материальную точку массы m кроме гравитационной силы (2.53) действуют другие силы, в результате чего она движется по определенной траектории С. Найдем работу гравитаци-
онной силы f при перемещении материальной точки по траектории из точки
1 в точку 2. Сила f является переменной силой, так как при движении массы
m по траектории С общего вида изменяется величина силы согласно (2.53), а также направление. На основании (2.32) работа силы (2.53) при перемещении материальной точки может быть записана в виде:
A12 = ∫ |
f cosα dS, |
c |
|
где α — rугол между вектором f , который в данном случае направлен против вектора r , проведенного от массы М к материальной точке, и вектором пере-
мещения dS . Заметим, что произведение cosα dS, стоящее под знаком интеграла в последнем выражении, может быть записано следующим образом:
cosα dS = −cosβ dS = −dr, |
(2.54) |
где угол β дополняет угол α до π, а dr представляет собой изменение расстояния между массами m и М при элементарном перемещении dS материальной точки по траектории С. Используя равенство (2.54) и приведенное
81
выше выражение для работы А12, а также (2.53), запишем работу силы f в следующем виде:
r2 |
Mm |
dr , |
(2.55) |
|
A12 = −∫G |
r |
2 |
||
r1 |
|
|
|
|
где r1 и r2 — расстояния между массой М (или ее центром, когда она представляет собой шар) и точками 1 и 2 соответственно. Таким образом, в данном случае нахождение работы переменной силы (2.32) с помощью криволинейного интеграла привело к определенному интегралу (2.55), в результате вычисления которого получим:
A = G Mm |
−G Mm . |
(2.56) |
|
12 |
r2 |
r1 |
|
|
|
||
Формула (2.56) показывает, что работа А12 выражается одинаково для всех возможных траекторий, соединяющих точки 1 и 2, так как в это выражение входят только характеристики точек 1 и 2, это r1 и r2, и не входят координаты или другие характеристики промежуточных точек траектории. На основании этого результата можно сделать вывод о том, что силы гравитационного притяжения к точечной (или сферической) массе М консервативны. Можно показать также, что консервативным является поле произвольной системы неподвижных тел.
Гравитационное поле точечной или сферической массы является частным случаем так называемых центральных полей. Центральным называется такое поле, в котором выполняются два следующих условия: вектор силы в каждой точке пространства направлен по прямой, соединяющей эту точку с определенной выделенной точкой поля О (центр поля); величина силы в каждой точке пространства зависит только от расстояния между этой точкой и выделенной точкой О, f = f (r).
На основании приведенного выше доказательства консервативности гравитационных сил можно утверждать, что все центральные поля являются
консервативными полями. Действительно, пусть центральная сила f дейст-
вует на материальную точку массой m (рис. 2.6, где изображена центральная сила отталкивания). При произвольном виде функции f(r) элементарная работа этой силы
δA = f (r) dS = f (r)cosα dS = f (r)dr, |
(2.57) |
так как на основании свойств центральных сил угол α является углом между
вектором перемещения dS и радиальной прямой, и в результате dS cosα = ±dr («+» — в случае силы отталкивания, «−» — силы притяжения). Исходя из (2.57), работу центральной силы f (r) на участке траектории между точками 1 и 2 записываем в следующем виде:
82

|
r2 |
|
A12 = ∫ f (r)dr = ∫ f (r)dr =Φ(r2 ) −Φ(r1). |
(2.58) |
|
c |
r1 |
|
где Ф(r1) и Ф(r2) — определенные функции r, вычисленные в точках 1 и 2. Характеристики других точек траектории материальной точки в окончательное выражение работы (2.58) не входят. Поэтому можно утверждать, что центральные поля сил консервативны. (Ограничиваемся рассмотрением
стационарного случая, т.е. считаем, что сила f не зависит от времени.) Пример 2. Поле сил тяжести является частным случаем гравитационного
поля Земли, когда расстояние от точек поля до поверхности Земли намного
меньше радиуса Земли. В таком случае величину r, входящую в формулу (2.53) и представляющую собой расстояние между материальной точкой массой m и центром Земли, можно считать постоянной, равной радиусу Земли Rз. При этом условии и без учета вращательного движения Земли силу притяжения к Земле, действующую на каждую материальную точку (или тело) массой m , помещенную над ее поверхностью, на основании формулы (2.53) можно записать в
следующем виде:
|
Рис. 21 |
|
M ç |
|
|
f = mgr, |
g =G |
, |
|
|
RÇ2 |
|||
|
|
|
|
|
Мз — масса Земли. Сила |
f в этом |
случае называется силой тяжести, |
||
gr |
— ускорением свободного падения, которое будем считать одинаковым |
|||
по величине и направлению во всех точках выделенной части пространства над поверхностью Земли при условии h << Rз (h − высота над поверхностью Земли). При отмеченных выше условиях сила тяжести f и ускорение свободного падения gr направлены к центру Земли, т.е. вертикально.
Весом материальной точки (тела) называется сила, с которой тело действует на опору или подвес благодаря силе тяжести.
Чтобы выяснить, является ли сила тяжести консервативной, необходимо вычислить работу этой силы при перемещении материальной точки массой m из точки 1 в точку 2 по произвольной траектории (рис. 2.7). Элементарная
работа силы тяжести при перемещении dS записывается в виде:
Рис 2.7
δA = mgr dS = mg cosα dS ,
83
где α — угол между векторами gr и dS . Как видно из рис. 2.7, произведение
cosα dS равно элементарному изменению расстояния между точкой и поверхностью Земли, т.е. высоты h с противоположным знаком. В случае, изображенном на рис. 2.7, cos α > 0 ; при удалении от поверхности Земли
dh >0, cos α < 0 . В каждом случае cosα dS = −dh. Учитывая это, элементар-
ную работу силы тяжести представляем в виде:
δA = −mgdh .
Работа силы тяжести при перемещении материальной точки по траектории С
из точки 1 в точку 2
2
A12 = −∫mgdh = mg(h1 − h2 ) , (2.59)
1
где h1 и h2 – расстояния между поверхностью Земли и точками 1 и 2 соответственно. Результат (2.59) свидетельствует, что работа силы тяжести при перемещении материальной точки (тела) из точки 1 в точку 2 не зависит от траектории, соединяющей эти точки, а только от местоположения точек 1 и 2. Тем самым показано, что сила тяжести является консервативной силой.
Поле сил тяжести является частным случаем однородного поля сил. Поле сил называется однородным, если величина и направление векто-
ра силы во всех точках данной части пространства одинаковы. Пример доказательства консервативности силы тяжести позволяет утверждать, что все однородные поля сил консервативны. Действительно, при вычислении работы в однородном поле сил по формуле, аналогичной (2.59), постоянную величину силы (как mg в приведенном случае) можно вынести за знак интеграла и получить результат, аналогичный (2.59).
Пример 3. Докажем консервативность сил упругости на примере упругой пружины. Пусть растянутая до величины деформации x1 (удлинение)
упругая пружина под действием сил упругости сжимается до величины деформации x2 . Как известно, проекция силы упругости на ось X, выбранную
вдоль пружины, Fxóïð = −kx . Для определения работы этой силы можно воспользоваться формулой (2.34), которая получена для работы внешней силы F , противоположной силе упругости, Fx = −Fxóïð . C учетом этого работа силы упругости пружины при ее деформации от удлинения x1 до x2
A |
= |
kx |
2 |
kx |
2 |
(2.60) |
1 − |
2 . |
|||||
12 |
|
2 |
|
2 |
|
|
|
|
|
|
|
||
Формула (2.60) показывает, что работа сил упругости при деформации упругой пружины не зависит от траектории или способа, при котором пружина от состояния 1 пришла в состояние 2. Например, растягивание пружины от x1 до x2 может проходить непосредственно (через все промежуточные
состояния) или пружина была сначала растянута до удлинения x3 > x2 , а по-
84

том сжата до x2 и т.д. Во всех указанных случаях работа сил упругости опре-
деляется формулой (2.60) и, значит, имеет одну и ту же величину. Тем самым показано, что силы упругости консервативны.
Можно дать еще одно, эквивалентное двум предыдущим, определение консервативности сил. Для этого покажем, что если поле консервативно, то работа по пермещению материальной точки по замкнутой траектории равна нулю. Действительно, пусть материальная точка массой m движется в кон-
сер-вативном поле сил f (x, y, z) по замкнутой траектории (рис. 2.8). Выде-
лим на траектории две произвольные точки В и D и обозначим часть траектории от точки В до точки D буквой С, а от точки D до точки В — буквой L.
Работу консервативной силы f по замкнутой траектории можно записать в виде суммы двух частей:
А = ABCD + ADLB |
(2.61) |
Работа по траектории DLB равна с противоположным знаком работе при перемещении материальной точки по той же самой траектории, но в противоположном направлении.
Справедливость этого утверждения вытекает из того, что элементарная работа при перемещении dS по траектории DLB (рис. 2.1)
|
r |
→ |
|
|
δADLB = f |
dS = f cosα dS, |
|
|
|
→ |
→ |
а элементарная работа при перемещении dS |
′ = −dS по той же траектории, но |
||
в противоположном направлении |
|
|
|
r |
→ |
|
|
δABLD = f |
dS′= f cos(π−α)dS = − f cosα dS. |
||
Рис. 2.8
Два последних равенства показывают, что эти элементарные работы отличаются только знаком, а поэтому
85

ADLB = −ABLD . |
(2.62) |
Подставляя (2.62) в (2.61), получим |
|
А = АBCD − ABLD |
(2.63) |
Но работы ABCD и ABLD равны друг другу, так как они представляют собой работы консервативной силы f по двум траекториям, соединяющим точки B и
D. Поэтому окончательно, работа консервативной силы по замкнутой траектории
А = ∫ f dS = 0, |
(2.64) |
(кружок на знаке интеграла означает, что интеграл берется по замкнутой траектории). Условие (2.64) полностью эквивалентно тому, что работа сил, приложенных к материальной точке или телу, не зависит от формы траек-тории, соединяющей две точки в пространстве. Другими словами, (3.39) яв-ляется необходимым и достаточным условием консервативности сил. Поэ-тому возможно еще одно определение консервативных сил: поле сил консервативное, если работа этих сил при перемещении по замкнутой траектории равна нулю.
3.2.2.4 Потенциальная энергия материальной точки во внешнем силовом поле
Для материальной точки или тела, находящихся в консервативном поле сил, можно ввести понятие потенциальной энергии. Каждому положению материальной точки в консервативном поле сопоставим определенное значение некоторой функции Wп (x,y,z) следующим образом: выберем определенную точку О, припишем материальной точке, если она находится в точке О, значение этой функции Wï o (Рис. 2.9). Будем считать, что при
нахождении материальной точки в точке 1 соответствующее значение Wï 1 определяется
следующим равенством:
Рис 2.9
Wï 1 =Wï 0 + A10,
где A10 – работа консервативной силы поля при перемещении в нем матери-
альной точки из точки 1 в точку О по произвольной траектории. Точке 2 припишем такое значение функции Wï 2 , чтобы
Wï 2 =Wï 0 + A20 и т.д.
86
Разность значений функции Wï в точках 1 и 2 |
|
Wï 1 −Wï 2 = A10 + A02. |
(2.65) |
При написании равенства (2.65) было использовано то, что A20 = −A02 по од-
ной и той же траектории. Сумма работ, стоящих в правой части (2.65), представляет собой работу сил поля при перемещении материальной точки из
точки 1 в точку 2 через точку О. На основании консервативности сил поля это есть работа A12 при перемещении материальной точки по произвольной
траектории, соединяющей точки 1 и 2. Поэтому вместо (2.65) имеем с учетом равенства (2.32):
W |
−Wï 2 |
= A12 = ∫ f dS . |
(3.42) |
ï 1 |
|
C |
|
Приходим к выводу, что в консервативном поле сил каждому положению материальной точки можно сопоставить определенное значение функции координат Wï (x,y,z) таким образом, чтобы разность значений этой функции в
двух точках поля (1 и 2) была равна работе сил поля при перемещении материальной точки по произвольной траектории, соединяющие эти точки. Заданная таким способом функция координат называется потенциальной энергией материальной точки в консервативном поле сил. Разность потенциальных энергий, стоящая в левой части (2.65), сокращенно записывается следующим образом:
Wï 1 −Wï 2 = − Wï , |
(2.66) |
где Wï =Wï 2 −Wï 1 – изменение функцииWï . Величина (2.66) называется
убылью потенциальной энергии. Используя это понятие, даем следующее определение потенциальной энергии: потенциальная энергия материальной точки во внешнем поле консервативных сил — это та энергия, убыль которой при переходе материальной точки из точки 1 в точку 2 равна работе консервативных сил при перемещении по произвольной траектории, соединяющей эти точки. Из этого определения вытекает, что потенциальная энергия — это скалярная алгебраическая величина, она выступает только в случае консервативности сил, действующих на материальную точку (тело).
На основании определения потенциальной энергии найдем конкретные аналитические ее выражения в частных случаях, рассмотренных в предыдущем пункте.
1. Работа сил гравитационного поля, созданного точечной массой (или шаром) М при перемещении материальной точки массы m записывается формулой (2.56). Объединяя (2.56) с (2.66), получим
A = G Mm |
−G Mm =W |
−W |
, |
(2.68) |
|
12 |
r2 |
ï 1 |
ï 2 |
|
|
|
r1 |
|
|
|
|
87
где Wï 1 и Wï 2 — потенциальные энергии материальной точки в гравитацион-
ном поле точечной или шаровой массы в точках 1 и 2 соответственно. Равенства (2.66) вообще и (2.68) в частности дают возможность определить не потенциальную энергию в отдельной точке, а только разность потенциальных энергий в двух определенных точках. Чтобы найти потенциальную энергию в одной отдельной точке, надо принять дополнительное условие, задавая определенное значение потенциальной энергии в определенной точке пространства. В данном случае гравитационного поля принимается следующее дополнительное условие: Wï 2 → 0, если r2 → ∞. Это означает, что при бесконеч-
ном удалении от массы, создающей поле, потенциальная энергия должна стремиться к нулю. При этом условии из (2.68) получим:
W |
= −G Mm |
, |
|
ï 1 |
r2 |
|
|
|
1 |
|
|
или вообще |
|
|
|
W = −G Mm. |
(2.69) |
||
ï |
r |
|
|
|
|
|
|
Как видно из (2.69), потенциальная энергия материальной точки массы m в поле массы М отрицательная, если ее принять равной нулю на бесконечности.
2. Для поля силы тяжести из (2.59) и (2.66) получим:
A12 = mg(h1 −h2 ) =Wï 1 |
−Wï 2 . |
(2.70) |
Чтобы от разности потенциальных энергий материальной точки перейти к ее значению в определенной точке, в данном случае принимаем следующее дополнительное условие: Wï 2 = 0 при h2 = 0. С учетом этого из (2.70) следует
Wï 1 = mgh1 .
или |
|
|
|
|
|
|
|
|
|
|
|
|
Wï |
= mgh. |
(2.71) |
||||
3. |
Работа сил упругости при деформации пружины определяется |
||||||||
формулой (2.60), которая вместе с (2.66) приводит к равенству: |
|||||||||
|
A = |
kx |
2 |
− |
kx |
2 |
2 |
=W |
−W . |
|
1 |
|
|
|
|||||
|
|
|
|
|
|
||||
|
12 |
2 |
|
|
2 |
ï 1 |
n2 |
||
|
|
|
|
|
|
|
|||
Выбираем естественное дополнительное условие, состоящее в том, что потенциальная энергия недеформированной пружины равна нулю, т.е.Wï 2 = 0
при x2 = 0 . Учитывая это, получим из (2.72) следующую формулу для потенциальной энергии деформированной пружины:
88
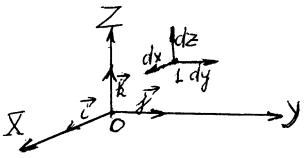
W = kx2 , (2.73)
ï |
2 |
|
где x — величина деформации пружины (удлинение).
Формула (2.66) выражает связь между потенциальной энергией материальной точки в консервативном поле сил и работой этих сил. Найдем связь между потенциальной энергией и консервативной силой. С этой целью запишем равенство, соответствующее (2.66) для элементарного перемещения
→
dS материальной точки: |
|
||
δA = −dWï . |
(2.74) |
||
Элементарная работа δA выражается формулами (2.28). Используя од- |
|||
ну из них, из (2.74) получим: |
|
||
dWï = − fSdS, |
(2.75) |
||
откуда |
|
||
fS = − |
dWï |
. |
(2.76) |
|
|||
|
dS |
|
|
Формула (2.76) проясняет связь между потенциальной энергией и консервативной силой, а именно: проекция вектора консервативной силы на произвольное перемещение равна с противоположным знаком изменению потенциальной энергии материальной точки при перемещении на единичное
расстояние в выбранном направлении. Производная |
dWï |
, |
точнее |
∂Wï |
, |
|
dS |
∂S |
|||||
|
|
→ |
|
|||
|
|
|
|
|
называется производной функции Wï (x, y, z) в направлении вектора dS .
Очевидно, что наибольшую проекцию вектор f имеет на свое собствен-
ное направление. Поэтому из (2.76) вытекает, что наибольшая скорость изменения потенциальной энергии Wï существует вдоль линии силы. Другими
словами, сила f направлена в сторону наибольшего изменения потенциальной энергии. Знак минус в (2.76) показывает, что вектор f направлен в сто-
рону |
наибольшего |
уменьшения |
потенциальной |
энергии. |
|
Действительно, если |
fS > 0 , то |
|
dWï < 0 , т.е. Wï 2 <Wï 1 . |
|
|
Связь (2.76) можно представить в другом виде. Пусть материальная
Рис 2.10
89
точка переместилась в консервативном поле сил из начальной точки 1 вдоль оси X на расстояние dx (рис. 2.10). В этом случае формула (2.76) приобретает следующий вид:
fx |
= − |
dWï |
. |
(2.77) |
|
||||
|
|
dx |
|
|
Если материальная точка переместилась из точки 1 вдоль оси Y на dy , то из (2.76) будет следовать:
fy |
= − |
dWï |
. |
(2.78) |
||
|
|
|||||
|
|
|
dy |
|
||
Наконец, при перемещении dz из точки 1 в направлении оси Z получим: |
||||||
fz |
= − |
dWï |
. |
(2.79) |
||
|
||||||
|
|
|
dz |
|
||
С помощью равенств (2.77) − (2.79) и единичных векторов i , j,k |
системы |
|||||
координат запишем вектор силы f . Учтем также то, что производные по-
тенциальной энергии в указанных равенствах являются фактически частными производными функцииWï (x, y, z) . В результате вектор консервативной
силы запишется следующим образом:
r |
|
∂W |
r |
|
∂W |
r |
|
∂W |
r |
|
|
f |
= − |
ï |
i |
− |
ï |
j |
− |
ï |
k. |
(2.80) |
|
∂x |
∂y |
∂z |
|||||||||
|
|
|
|
|
|
|
|
Равенство (2.80) выражает специфическую связь между скалярной величиной потенциальной энергии материальной точки во внешнем консервативном поле сил и консервативной силой (векторной величиной). Если, вообще говоря,
определенная скалярная функция ϕ(x, y, z) и векторная функция b(x, y, z)
связаны друг с другом таким образом, что проекции вектора b на оси координат равны соответствующим частным производным функции ϕ, т.е.
b |
= |
∂ϕ |
, |
b |
= |
∂ϕ |
, |
b |
= |
∂ϕ |
, то говорят, что вектор b является градиен- |
|||
x |
|
∂x |
|
y |
|
∂y |
|
z |
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
том скаляра ϕ и записывают: |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
br |
→ |
||
|
|
|
|
|
|
|
|
|
|
|
= gradϕ. |
|||
В нашем случае вектор силы f выражается подобным образом через частные производные потенциальной энергии Wï , но со знаком минус. Поэтому окончательно
90
fr |
→ |
|
= −gradWï |
(2.81) |
Выражение (2.81) является условной записью совокупности равенств (2.77) — (2.79). Вектор f направлен, как уже отмечалось, в сторону наиболее
быстрого изменения, а именно — уменьшения потенциальной энергии. Заметим, что (2.80) представляет собой первое определение консерва-
тивных сил (см.( 2.52)), если U = −Wï . Используя (2.80), элементарную работу δА можно записать в виде:
r |
→ |
|
∂W |
∂W |
∂W |
|
= −dW . (2.82) |
δA = f |
dS = − |
ï dx+ |
ï dy+ |
ï dz |
|||
|
|
|
∂x |
∂y |
∂z |
|
ï |
|
|
|
|||||
Формула (2.82) означает, что в случае консервативности сил элементарная работа есть полный дифференциал функции (−Wï ), это еще одно определе-
ние консервативности сил: сила является консервативной, если элементарная работа этой силы есть полный дифференциал определенной функции.
3.2.2.5 Понятие о потенциальной энергии взаимодействия
Обратим внимание на энергию взаимодействия между материальными точками с массами m1 и m2 . Силы взаимодействия могут быть консерватив-
ными или неконсервативными. Легко показать, что если они обладают свойствами, подобными свойствам центральных сил, а именно: силы направлены вдоль прямой, соединяющей точки, и их величина зависит только от расстояния между материальными точками, — то такие силы взаимодействия будут консервативными в указанном выше смысле. Действительно, пустьr две мате-
риальные точки взаимодействуют с силами отталкивания f12 и f21 (Рис. 2.11). Величины сил по третьему закону Ньютона — f12 = f21 ; эти си-
лы направлены вдоль соединяющей материальные точкиr прямойr . Пусть величина этих сил зависит от расстояния между точками; r1 и r2 — радиус-
векторы материальных точек, проведенные из начала координат О. Вектор
R |
= rr −rr |
|
имеет величину R12 , равную расстоянию между массами m и |
||||||||||||||||
12 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
m2 |
и направлен от m1 к m2 . При движении материальных точек изменяются |
||||||||||||||||||
векторы r1 |
|
|
и r2 |
и, вместе с этим, |
R12 .Найдем работу сил взаимодействия |
||||||||||||||
fr12 |
и f21 . |
|
|
Сумма элементарных работ этих сил запишется цепочкой ра- |
|||||||||||||||
венств: |
|
|
|
|
|
|
|
|
|
|
drr + f |
|
drr |
|
|
(drr |
−drr ) = |
|
|
|
δA = δA |
+δA |
= f |
|
|
= f |
|
(2.83) |
|||||||||||
|
r |
|
|
12r |
r21 |
r12 |
r1 |
21 |
2 |
|
12 |
1 |
2 |
||||||
|
= f |
12 |
d(r |
−r ) = f |
12 |
dR . |
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
2 |
|
|
|
12 |
|
|
|
|
|
|
|
|||
91
Последнее скалярное произведение можно записать с помощью проекции
→ |
|
|
|
|
|
|
вектора dR12 на направление f12 : |
|
|
|
|||
|
|
|
→ |
→ |
|
|
|
|
|
fr12 dR12 |
= f12 (dR12 ) f . |
|
Rr |
Проекция |
(dR12 ) f |
представляет собой изменение модуля вектора |
||||
|
|
12 , |
||||
т.е. dR12 , так как сила |
f12 направлена по той же прямой, что и R12. Учитывая |
|||||
это, запишем элементарную работу сил взаимодействия в следующем виде: |
|
|||||
|
|
|
δA = − f12dR12 . |
(2.84) |
||
Так же, как в случае центральных сил, выражение (2.84) для элементарной работы ведет к независимости работы сил взаимодействия между двумя материальными точками при переходе этой механической системы из состояния 1 в состояние II по траекториям этих точек:
АI II = − II∫ f12dR12 = −[Φ(R12 )II − Φ(R12 )I ]. |
(2.85) |
I |
|
Таким образом, силы взаимодействия при двух указанных выше условиях являются консервативными. Функция Ф(R12) является потенциальной энергией взаимодействия материальных точек. (2.85) означает, что работа сил взаимодействия при перемещении взаимодействующих точек равна разности потенциальных энергий взаимодействия:
|
АI II =Wïâç1 −Wïâç1 . |
(2.86) |
Явный вид функции |
W âç зависит от характера сил взаимодействия |
f . На- |
|
ï |
|
пример, если величина силы взаимодействия обратно пропорциональна квадрату расстояния между материальными точками, то
f (R12 ) = |
α |
, |
α = const, |
|
R2 |
||||
|
|
|
||
|
12 |
|
|
что выполняется для гравитационных сил, а также для кулоновского взаимодействия заряженных материальных точек, то формула (2.85) ведет к следующему выражению для работы этих сил:
АI II = −II |
f (R )dR |
= −αII |
dR12 |
= |
α |
− |
α |
=W |
âç −W âç |
, |
||
|
|
|
||||||||||
∫ |
12 12 |
∫ |
R122 |
|
(R12 )II |
|
(R12 )I |
ï |
1 |
ï |
2 |
|
I |
|
I |
|
|
|
|
|
|||||
где (R12 )I и (R12 )II — расстояния между материальными точками в первоначальном (I) и конечном (II) состояниях системы. Если принять условие, что при (R12 )II → ∞ WïIIâç →0, получим
92

W âç = − |
α |
. |
(3.63) |
ï R12
В случае притяжения α > 0, в случае отталкивания α < 0.
Для трех материальных точек потенциальная энергия взаимодействия складывается из энергий взаимодействия каждых двух точек между собой:
Wïâç =Wïâç12 +Wïâç13 +Wï23âç .
Рис. 2.11
3.2.2.6Закон сохранения механической энергии
Впоследних пунктах основное внимание было уделено консервативным силам, действующим на материальную точку cо стороны внешнего поля сил или между каждыми двумя материальными точками. Но не все силы в природе консервативные, например, неконсервативная — сила тяги автомобиля. Типичными неконсервативными являются так называемые диссипативные силы — работа которых отрицательна при любом перемещении материальной точки. Это силы трения, силы сопротивления движению тела в газах и жидкостях. Сила трения скольжения, например, действующая со стороны неподвижного тела на движущееся тело, всегда направлено в сторону, противоположную движению тела. Поэтому работа этой силы по произвольной, в том числе и замкнутой, траектории отрицательна.
Введем в рассмотрение полную механическую энергию системы.
Полной механической энергией (механической энергией) системы N материальных точек (тел) называется сумма кинетических энергий всех материальных точек (тел), их потенциальных энергий во внешнем поле сил, а также потенциальных энергий взаимодействия материальных точек (тел) между собой. В соответствии с этим определением все силы, действующие на матери-
альную точку системы массой m, разделим на 4 класса: fi — консервативная внутренняя сила или их равнодействующая, если их несколько; fri — некон-
93
сервативная внутренняя сила или их равнодействующая, если их несколько;
Fi — консервативная сила во внешнем силовом поле или их равнодейст-
вующая; Fri — неконсервативная сила во внешнем силовом поле или их
равнодействующая. На основании теоремы о кинетической энергии системы материальных точек (2.46) изменение кинетической энергии системы материальных точек за определенный промежуток времени t =t2 −t1 равно ра-
боте всех сил, приложенных ко всем точкам системы:
Wk |
−Wk |
= A |
âñåõ |
= A |
внутр |
внутр |
+ A |
âíåø |
âíåø |
, |
(2.88) |
|
|
+ A |
|
+ A |
|||||||
|
2 |
1 |
|
|
|
|
|
|
|
|
|
где Aвнутр и |
A внутр − работа внутренних консервативных и неконсерватив- |
||||||||||
ных сил соответственно, Aâíåø и À âíåø — работа внешних консервативных и неконсервативных сил. В соответствии с определением работа консервативных сил за промежуток времени равна разности соответствующих значений потенциальных энергий в начале и в конце этого промежутка времени. Поэтому можно написать:
|
Àвнутр =W âç −W âç , |
Àâíåø =W |
−W , |
(2.89) |
|
|
ï 1 |
ï 2 |
ï 1 |
ï 2 |
|
где W âç и W âç − суммы потенциальных энергий взаимодействия материаль- |
|||||
ï 1 |
ï 2 |
|
|
|
|
ных точек системы между собой в моменты времени t1 и t2 соответственно; Wï 1 и Wï 2 — суммы потенциальных энергий всех материальных точек сис-
темы во внешнем поле сил в моменты времени t1 и t2. Подставляя (2.89) в (2.88), получим:
W |
|
−W =W |
|
âç |
−W |
âç |
внутр |
+W |
|
|
âíåø |
. (2.90) |
|
ï |
|
|
+ A |
|
−W + À |
||||||
k |
2 |
k |
1 |
ï 2 |
|
ï |
1 |
ï |
2 |
|
||
|
1 |
|
|
|
|
|
|
|
||||
Преобразуем (2.90), перенося все потенциальные энергии в левую сторону равенства и группируя слагаемые по моментам времени:
(W |
|
+W |
âç +W ) −(W +W âç +W |
ï |
) = A внутр + A âíåø . (2.91) |
|||||
k |
2 |
ï |
2 |
ï |
2 |
k |
ï |
1 |
1 |
|
|
|
|
1 |
|
|
|||||
В первых скобках (2.91) записана полная механическая энергия системы в момент времени t2, которую обозначим Wìåõ 2 . Во вторых скобках, соответст-
венно, стоит полная механическая энергия системы в момент времени t1, т.е. Wìåõ 1 . Равенство (2.91) приобретает вид:
W =W |
−W |
= A внутр + A íåø . |
(2.92) |
ìåõ |
ìåõ 2 |
ìåõ 1 |
|
Выражение (2.92) представляет собой закон изменения полной механической энергии системы: изменение полной механической энергии системы материальных точек (или тел) равно работе всех неконсервативных сил, внутренних и внешних, действующих на все точки системы.
94

Возникает вопрос, в каком случае полная механическая энергия системы с течением времени остается постоянной. Ответ на него следует из (2.92): полная механическая энергия системы материальных точек остается постоянной, если на точки системы действуют только консервативные силы (внутренние и внешние). При этом условии À внутр . = À âíåø = 0, и из (2.92) получаем:
Wìåõ = 0, |
|
или |
|
Wìåõ 1 =Wìåõ 2 = const. |
(2.93) |
Полученный результат представляет собой закон сохранения механи- ческой энергии. Если на точки системы действуют неконсервативные силы,
например сила трения, то работа |
A |
внутр . |
≠ 0 |
âíåø |
≠ 0 и, в соответствии |
|
или À |
с (2.92), механическая энергия системы изменяется. Если À < 0 , как для силы трения, то Wìåõ < 0, т.е. Wìåõ 2 <Wìåõ 1 , механическая энергия превраща-
ется в другие, немеханические виды энергии. В этом случае имеем диссипацию энергии.
Частным случаем механической системы является замкнутая механическая система N материальных точек, т.е. такая система, на которую не действуют внешние силы. Для замкнутой системы À âíåø = Àâíåø = 0, благодаря чему (2.92) переходит в следующее равенство:
W =W |
ìåõ 2 |
−W |
= A внутр . . |
ìåõ |
ìåõ 1 |
|
Из него следует, что механическая энергия замкнутой системы остается постоянной, если все внутренние силы консервативны:
À внутр = 0 |
, W = 0, W |
ìåõ 2 |
=W |
. |
(2.94) |
|
ìåõ |
ìåõ 1 |
|
|
Заметим, что мы рассматривали только стационарный случай, т.е. при условии независимости сил от времени.
3.3ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ
3.3.1Применение законов сохранения импульса и энергии к абсолютно упругому и абсолютно неупругому ударам
Ударом называется явление изменения скоростей тел на конечные значения за очень малый промежуток времени их столкновения. Общая нормаль к поверхностям соударяющихся тел в точке их соприкосновения называется линией удара. Удар называется прямым, если перед ударом скорости цен
95

тров масс соударяющихся тел параллельны линии удара. Удар называется центральным, если тела до удара движутся вдоль прямой, проходящей через их центры масс. Удары двух шаров одинакового радиуса, катящихся по горизонтальной плоскости так, что их центры движутся по одной прямой, являются прямыми и центральными (рис. 2.12, а). Прямой центральный удар двух шаров различных радиусов можно осуществить, подвесив шары на нитях таким образом, чтобы их центры масс были на одной горизонтали (рис. 2.12, б).
m1 υr10 υr20 m2
а) |
m1 |
m2 |
|
υ10 |
υ20 |
|
|
|
б) |
m1 |
υ10τ υ10n |
|
|
υ20 |
υ10 |
|
|
υ20n |
υ20τ m2 |
|
|
|
в) |
Рис. 2.12
При соударении тел друг с другом они претерпевают деформации. При этом кинетическая энергия, которой обладали тела перед ударом, может частично или полностью переходить в потенциальную энергию упругой деформации и внутреннюю энергию тел. Увеличение внутренней энергии тела сопровождается увеличением его температуры.
Существуют два предельных вида ударов: абсолютно упругий и абсолютно неупругий.
Абсолютно упругим называется такой удар, при котором механическая энергия тел не переходит в другие, немеханические виды энергии. Во время такого удара кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. После этого тела возвращаются к первоначальным размерам и форме, взаимно отталкиваясь друг от друга. В результате потенциальная энергия упругой деформации снова переходит в кинетическую энергию, и тела расходятся со скоростями, которые определяются двумя законами: законом сохранения механической энергии и законом сохранения импульса системы тел. Механическая энергия остается постоянной в данном случае потому, что силы упругости, действующие при ударе, консервативны.
Абсолютно неупругий удар характеризуется тем, что потенциальная энергия упругой деформации не возникает; кинетическая энергия тел полностью или частично превращается во внутреннюю энергию; после удара столкнувшиеся тела либо движутся с одинаковой скоростью, либо покоятся.
При рассмотрении ударов система тел не является замкнутой, так как на каждое тело действует сила тяжести и сила реакции опоры или подвеса. Тем не менее, к любому удару можно применить закон сохранения проекции импульса на ось, перпендикулярную указанным силам.
96
В дальнейшем при рассмотрении абсолютно упругого и абсолютно неупругого ударов будем считать, что удар происходит между материальными точками или телами, движущимися поступательно. Рассматривая удар двух шаров, не будем учитывать их вращательного движения при качении.
1. Рассмотрим вначале абсолютно неупругий прямой центральный удар шаров. Пусть два шара с массами m1 и m2 движутся горизонтально вдоль одной
прямой с первоначальными скоростями υr10 и υ20 соответственно. Удар шаров происходит либо при их движении навстречу друг другу, либо если один
шар догоняет другой. |
|
|
|
На основании закона сохранения импульса можно записать: |
|
||
r |
+m2υ20 |
r |
(2.95) |
m1υ10 |
= m1υ+m2υ = (m1 +m2 )υ |
||
(сила тяжести каждого шара уравновешивается силой реакции опоры). |
|
||||||
r |
|
|
|
|
|
|
|
В равенстве (2.95) υ — одинаковая для обоих шаров скорость после удара: |
|||||||
r |
m υ |
+ m |
2 |
υ |
20 |
|
|
υ = |
1 10 |
|
|
. |
(2.96) |
||
|
|
|
|
|
|||
|
m + m |
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
Вычислим убыль механической энергии при абсолютно неупругом ударе, т.е. энергию, превратившуюся в немеханические виды энергии. Для этого от кинетической энергии шаров до удара отнимем их кинетическую энергию после удара:
|
|
|
m υ2 |
|
m |
υ2 |
(m + m |
)υ2 |
|
|
− |
W =W −W = |
1 10 |
+ |
2 |
20 |
− |
1 2 |
. |
(2.97) |
|
|
|
|
||||||||
|
k |
1 2 |
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
После подстановки (2.95) в (2.97) и элементарных преобразований получим:
− W = |
m1m2 |
(υ |
− υ |
20 |
)2 . |
(2.98) |
|
||||||
k |
2(m1+m2 ) |
10 |
|
|
|
|
|
|
|
|
|
|
Уменьшение механической энергии системы двух шаров сопровождается возрастаем внутренней энергии этой системы. В частности, если второе тело до удара покоится, υ20 = 0 , то относительное уменьшение кинетической
энергии системы
− |
Wk = |
m2 |
|
. |
(2.99) |
m + m |
|
||||
|
W |
2 |
|
|
|
|
k |
1 |
|
|
Втехнике используют абсолютно неупругий прямой центральный удар для изменения формы тел (ковка, штамповка, клепка и т.п.), для перемещения тел в среде с большим сопротивлением (забивание гвоздей, свай и т.п.).
Впервом случае целесообразно, чтобы отношение (2.98) было возможно ближе к 1, т.е., m2 >> m1 (масса отковываемого изделия и наковальни
должна во много раз превосходить массу молота).
Во втором случае, наоборот, нужно, чтобы потери кинетической энергии при ударе были возможно меньшими, т.е. m1>> m2 (масса молотка во
много раз должна превосходить массу гвоздя).
97
2. Рассмотрим применение законов сохранения импульса и механической энергии к расчету абсолютно упругого прямого центрального удара двух шаров с массами m1,m2 , движущихся до удара со скоростями υ10,υ20
соответственно. В данном случае упомянутые законы запишутся следующим образом:
r |
|
|
|
|
|
|
+ m2 |
υ2 |
, |
(2.100) |
||
m1υ10 + m2υ20 = m1υ1 |
||||||||||||
m υ2 |
|
m |
υ2 |
|
m υ2 |
|
m |
υ2 |
|
|
||
1 10 |
+ |
2 |
20 |
= |
1 1 |
|
+ |
2 |
2 |
, |
(2.101) |
|
2 |
2 |
2 |
2 |
|||||||||
|
|
|
|
|
|
|||||||
где υ1,υ2 — искомые скорости шаров после удара.
В проекции на ось X, совпадающую, например, с направлением скорости υ10 (рис. 2.12), уравнение (2.100) будет иметь вид:
m υ |
+ m |
υ |
20 |
= m υ + m |
υ |
2 |
, |
(2.102) |
|||
1 |
10 |
2 |
|
1 |
1 |
2 |
|
|
|
||
где алгебраические величины υ10 ,υ20 ,υ1,υ2 |
являются проекциями соответ- |
||||||||||
ствующих векторов на выбранную ось X. В уравнениях (2.100) и (2.102) сгруппируем слагаемые, имеющие множитель m1 , в левых частях равенств, а
множитель m2 — в правых частях равенств:
m1(υ10 −υ1) = m2 (υ2 −υ20 ) , |
(2.103) |
||||||
m (υ2 |
−υ2 ) = m |
2 |
(υ2 |
−υ2 |
) |
(2.104) |
|
1 |
10 |
1 |
2 |
20 |
|
|
|
(уравнение (2.101) одновременно умножили на 2). Разделив равенство (2.104) на равенство (2.103), получим:
υ10 + υ1 = υ2 + υ20 . |
(2.105) |
|||||||
Равенство (2.104) равносильно тому, что |
|
υ10 −υ20 |
|
= |
|
υ2 −υ1 |
|
. Послед- |
|
|
|
|
|||||
нее означает, что при абсолютно упругом прямом центральном ударе величина относительной скорости соударяющихся тел остается постоянной.
Далее, решая систему уравнений, состоящую из (2.103) и (2.104), относительно неизвестных величин υ1 и υ2 , получаем следующие окончательные
выражения: |
|
|
|
|
|
|
|
|
|
|
|
υ = |
υ10 (m1 −m2 ) + 2m2υ20 |
, |
υ |
2 |
= |
υ20 (m2 −m1) +2m1υ10 |
. |
(2.106) |
|||
|
|
||||||||||
1 |
|
m1 |
+ m2 |
|
|
|
m1 |
+m2 |
|
||
|
|
|
|
|
|
|
|||||
Проанализируем полученные результаты (2.106) для некоторых частичных случаев.
Если
а) соударяющиеся шары имеют одинаковые массы, m1=m2 , то
υ1 = υ20 , |
υ2 = υ10 . |
(2.107) |
В этом случае шары после удара «обмениваются» скоростями. В частности, если один из шаров с одинаковой массой до соударения покоится, то после удара он двигается с той скоростью, какую имел первоначально движущийся шар; первоначально движущийся шар оказывается неподвижным; б) если массы шаров разные, m1 ≠m2 , и до удара один из шаров поко-
ится, например, υ20 = 0 , то
98
υ = |
(m1 −m2 )υ10 |
, |
υ |
2 |
= |
2m1υ10 |
.; |
(2.108) |
||
|
|
|||||||||
1 |
m1 |
+ m2 |
|
|
|
m1 |
+m2 |
|
|
|
|
|
|
|
|
|
|
||||
в) если один из шаров имеет значительно большую массу, чем другой, и шар с большей массой покоится, т.е.
m1<< m2 , υ20 = 0 , |
|
то приблизительно можно считать, что |
|
υ1 = −υ10 , υ2 = υ20 . |
(2.109) |
Равенства (2.109) показывают, что направление скорости лёгкого шара после центрального абсолютно упругого удара о массивный неподвижный шар будет изменяться на противоположное. Данный частный случай можно применить для определения скорости шара после упругого удара о неподвижную стенку, которую можно принять за шар бесконечно большой массы
ибесконечного радиуса.
3.Рассмотрим косой абсолютно упругий удар двух шаров (рис. 2.12 в, где показан вид сверху на плоскость XY , по которой движутся шары).
Вданном случае спроектируем векторное равенство (2.100), выражающее закон сохранения импульса системы двух шаров, на следующие два направления: на направление касательной к поверхностям соприкасающихся шаров, лежащей в плоскости скоростей υ10,υ20 (проекции на это касательное
направление будут обозначены индексом τ), и на направление, перпендикулярное к этой касательной (эти проекции будут снабжены индексом n ):
m1υ10τ + m2υ20τ = m1υ1τ + m2υ2τ , |
(2.110) |
m1υ10n + m2υ20n = m1υ1n + m2υ2n . |
(2.111) |
Соотношение (2.101), выражающее равенство кинетических энергий системы шаров до и после удара, может быть представлено в виде:
m |
(υ2 |
+ υ2 |
) |
|
m |
2 |
(υ2 |
+ υ2 |
) |
|
m |
(υ2 |
+ υ2 |
) |
|
m |
2 |
(υ2 |
τ |
+ υ2 |
) |
|
1 |
10τ |
10n |
|
+ |
|
20τ |
20n |
|
= |
1 |
1τ |
1n |
|
+ |
|
2 |
2n |
|
, (2.112) |
|||
|
2 |
|
|
|
|
r 2 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поскольку длина вектора υ и его взаимно перпендикулярные проекции υτ и υn связаны соотношением υ2 = υ2τ +υ2n .
Получено только три уравнения — (2.110), (2.111), (2.112) для нахождения четырех неизвестных величин: υ1τ,υ1n ,υ2τ,υ2n . Однако задача в дан-
ном случае оказывается вполне разрешимой: удар абсолютно упруг, так что суммарная кинетическая энергия шаров при ударе не изменяется. Это значит, что силы трения, которые уменьшают кинетическую энергию шаров, в данном случае не действуют. Поэтому касательные составляющие скоростей соударяющихся тел остаются неизменными: υ1τ = υ10τ,υ2τ = υ20τ , и уравнение
(2.110) обращается в тождество.
Для нормальных составляющих скоростей шаров остаются уравнения:
m1υ10n + m2υ20n = m1υ1n + m2υ2n ,
99

m υ2 |
+ m |
υ2 |
= m υ2 |
+ m |
υ2 |
, |
(2.113) |
1 10n |
2 |
20n |
1 1n |
2 |
2n |
|
|
которые совпадают по виду с системой уравнений (2.100),(2.101) для скоростей при прямом центральном ударе. Поэтому нормальные составляющие скоростей тел при косом упругом ударе изменяются так же, как изменяются скорости тел при прямом центральном ударе, и искомые формулы для υ1n и
υ2n совпадают по форме с выражениями (2.106). Касательные составляющее скоростей при этом не изменяются.
В качестве примера рассмотрим косой упругий удар легкого шарика массы m о неподвижную массивную плиту массой M >> m (рис. 2.13), если скорость шарика υ0 направлена под углом α0 к нормали n к поверхности
плиты. Найдем скорость шарика υr после удара.
Согласно сказанному выше, составляющие скоростей шарика вдоль поверхности плиты (направление касательного вектора τ) υ0τ и υτ до и по-
сле удара должны быть одинаковыми: υτ = υ0τ . Для нормальных составляю-
щих его скоростей используем результаты рассмотрения случая в) абсолютно упругого прямого центрального удара, выраженные равенствами (2.109):
υn = −υ0n , υ2n = υ20n = 0 , |
(2.114) |
(последнее равенство относится к покоящейся плите). Равенства(2.114) показывают, что величина скорости шарика в результате удара остается постоян-
ной, т.к. υ2 = υ02 . Не изменяется также величина угла, образованного вектором скорости шарика и нормалью к плите, т.к.
|
tgα |
|
= |
υτ |
= |
υ0τ |
= tgα0 . |
(2.115) |
|
|
|||||||
|
|
|
|
υn |
|
υ0n |
|
|
|
|
|
|
|
|
|
|
υr0τ |
υ |
υn |
||
r |
α |
|
||||
n |
υ |
|||||
υ |
0 |
υ |
0 n |
|||
|
|
|
τ |
|||
τ
Рис. 2.13
100
4 МАТЕРИАЛЫ, ИСПОЛЬЗУЕМЫЕ В ПРОЦЕССЕ ОБУЧЕНИЯ
4.1 МАТЕРИАЛЫ К ЛЕКЦИЯМ
Лекция 1 «Динамика материальной точки и поступательного движения твердого тела»
План лекции
1.Законы динамики материальной точки (законы Ньютона, импульс материальной точки, импульс силы, второй закон Ньютона, записанный через импульс).
2.Закон изменения импульса механической системы. Закон сохранения импульса (доказать для общего случая).
3 Центр инерции системы материальных точек и закон его движения. Основной закон динамики поступательного движения абсолютно твердого тела (показать, что основной закон динамики поступательного движения твердого тела совпадает с законом динамики материальной точки).
Контрольные вопросы
1.В каком случае твердое тело движется поступательно, равномерно и прямолинейно?
2.Как движется материальная точка под действием постоянной силы?
3.Как зависит от времени импульс постоянной силы?
4.Как движется центр масс замкнутой системы материальных точек?
Лекция 2 «Работа и механическая энергия»
План лекции
1.Механическая работа. Работа переменной силы. Мощность (в качестве примера вычисления работы переменной силы найти работу по растяжению упругой пружины).
2.Кинетическая энергия механической системы. Теорема о механической энергии материальной точки и системы материальных точек (дать вначале понятие механической энергии).
3.Силовое поле. Консервативные силы (дать определения консервативности сил через потенциальную функцию, через работу силы; доказать, что гравитационное поле сил консервативно; ввести понятие центрального поля сил; показать, что в консервативном поле сил работа по замкнутой траектории равна нулю).
4.Потенциальная энергия материальной точки во внешнем силовом поле (ввести понятие потенциальной энергии как скалярной функции состояния, убыль которой равна работе консервативной силы; на основании этого
101
получить выражения для потенциальной энергии материальной точки в гравитационном поле точечной массы, записать аналогичные выражения для поля силы тяжести и поля упругих сил; найти связь между потенциальной энергией и консервативной силой в двух видах).
5.Понятие о потенциальной энергии взаимодействия.
6.Закон сохранения механической энергии (дать понятие полной механической энергии системы материальных точек, доказать закон изменения механической энергии и закон сохранения механической энергии; понятие диссипативных сил).
Контрольные вопросы
1.Чему равна работа силы тяжести при движении тела по горизонтальной плоскости?
2.Зависит ли кинетическая энергия тела от выбора системы отсчета?
3.Изменит ли действие внутренних сил системы ее кинетическую энергию?
4.Является ли сила тяги автомобиля консервативной силой?
5.Остается ли постоянной механическая энергия замкнутой системы тел, между которыми действуют силы трения?
Вопросы для самоконтроля
Iуровень (репродуктивный)
1.Формулировки законов Ньютона.
2.Сформулировать понятия: инерциальной системы отсчета, силы, массы, внешних и внутренних сил механической системы, замкнутой механической системы.
3.Дать определения импульса материальной точки или поступательно движущегося тела, импульса механической системы.
4.Формулировки закона изменения импульса системы и закона сохранения импульса системы.
5.Центр масс системы материальных точек и закон его движения.
6.Формулы для вычисления работы постоянной силы и работы переменной силы.
7.Мгновенная мощность.
8.Теоремы о кинетической энергии материальной точки, системы материальных точек; выражение для кинетической энергии материальной точки (поступательно движущегося тела).
9.Понятие силового поля, центрального и однородного силовых полей, консервативности сил (силового поля), примеры консервативных и неконсервативных сил.
10.Определение потенциальной энергии материальной точки во внешнем силовом поле через работу консервативных сил.
102
11.Аналитические выражения потенциальной энергии материальной точки в гравитационном поле, в поле силы тяжести, в поле сил упругости.
12.Связь между консервативной силой и потенциальной энергией.
13.Формулировка и аналитическая запись закона изменения механической энергии и закона сохранения механической энергии механической системы.
14.Понятие диссипации механической энергии.
15.Понятия абсолютно упругого и абсолютно неупругого ударов. Запись законов сохранения для указанных видов ударов и аналитические выражения для вычисления скоростей тел после ударов.
IIуровень (продуктивный)
1.Получить из второго закона Ньютона основной закон динамики материальной точки, выраженный через импульс.
2.Доказать закон изменения импульса и закон сохранения импульса для системы N материальных точек.
3.Получить из основного закона динамики материальной точки соответствующий закон для поступательно движущегося тела.
4.Получить закон движения центра масс системы материальных точек.
5.Вывести формулу работы переменной силы.
6.Доказать теорему о кинетической энергии.
7.Показать консервативность гравитационной силы, силы тяжести и силы упругости.
8.Получить связь между работой консервативной силы и потенциальной энергией в общем виде, формулы потенциальной энергии материальной точки во внешнем гравитационном поле сил, в поле сил тяжести и в поле сил упругости.
9.Доказать, что работа консервативной силы по замкнутой траектории равна нулю.
10.Получить связь между консервативной силой и потенциальной энергией.
11.Понятие потенциальной энергии взаимодействия материальных точек.
12.Доказать закон изменения механической энергии и закон сохранения механической энергии механической системы.
13.Исходя из законов сохранения импульса и механической энергии, вывести формулы для скоростей, полученных поступательно движущимися телами
врезультате абсолютно упругого и абсолютно неупругого ударов.
IIIуровень (творческий)
1.Показать, что произвольное центральное поле консервативно, произвольное однородное поле консервативно.
2.Показать, что при движении материальной точки во внешнем консервативном силовом поле поверхности, на которых потенциальная энергия материальной точки одинаковая (эквипотенциальные поверхности), перпендикулярны вектору силы в каждой точке.
103
3.Показать, что при определенных условиях силы взаимодействия между материальными точками консервативны.
4.Решить задачу косого удара тел (шаров) в простейших случаях.
4.2.МАТЕРИАЛЫ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ
4.2.1 ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
ИПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА. РАБОТА И МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
4.2.1.1 Законы Ньютона
Примеры решения задач
Задача 1 (уровень 1)
Тело массой m = 2 кг движется прямолинейно по закону S = A – Bt + + Ct2 – Dt3 (C = 2 м/с2, D = 0,4 м/с3). Определить силу, действующую на тело в конце первой секунды движения.
Дано: |
Решение: |
|
|
|
m = 2 кг |
По II закону Ньютона |
|||
S = A – Bt + Ct2 – Dt3 |
F = mar. |
|
|
|
C= 2 м/с2 |
При прямолинейном движении |
|||
D= 0,4 м/с3 |
a = dυ |
= d |
2 |
S . |
t = 1 c |
|
|||
|
dt |
dt2 |
||
|
a = 2C – 6Dt. |
|||
F — ? |
a(1) = 2 ×·2 – 6 × 0,4 × 1 = 1,6 (м/с2) |
|||
|
Тогда искомая величина: |
|||
|
F = 2 × 1,6 = 3,2 (Н) |
|||
|
Ответ: 3,2 Н |
|
|
|
|
|
|
|
|
Задача 2 (уровень 2)
На автомобиль массой 1 т во время движения действует сила трения, равная 0,1 силы тяжести, действующей на тело.
Определить коэффициент трения μ между автомобилем и наклонной
плоскостью, силу тяги F двигателя автомобиля, если известно, что автомобиль движется с ускорением a = 1 м/с2 вверх по наклонной плоскости, имеющей уклон 1 м на каждые 25 м пути.
104
Дано: |
|
Решение: |
m = 1000 кг |
|
|
Fтр = 0,1 mg |
у |
|
a = 1 |
м/с2 |
x |
h = 1 |
м |
|
S = 25 м |
|
|
μ — ? |
|
|
F — ? |
|
Рис. 2.14 |
|
|
|
На автомобиль (рис 2.14) действуют 4 силы: сила тяжестиr mg , направ-
ленная вертикально вниз; сила реакции наклонной плоскости N , направленная перпендикулярно плоскости; сила тяги двигателя автомобиля, направленная по движению автомобиля вверх по наклонной плоскости; сила трения Fтр, направленная против движения, т.е. вниз по наклонной плоскости.
По II закону Ньютона:
mar = mgr + N + F + Fòð .
Выберем оси координат: OX — вдоль движения автомобиля, OY — перпендикулярно наклонной плоскости.
Спроецируем полученные уравнения на оси координат:
OX : ma = −mg sin α + F − Fòð ,
OY : 0 = −mg cosα + N .
Из второго уравнения этой системы выразим силу реакции опоры:
|
|
|
|
|
|
|
|
N = mg cosα. |
|
|
|
||||||||||||
|
По определению сила трения равна |
Fòð = μN . |
|
||||||||||||||||||||
Из двух последних уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
Fòð = μmg cosα. |
|
|
|
||||||||||||||
|
μ = |
|
|
Fòð |
= |
|
0,1mg |
|
= |
|
0,1 |
. |
|||||||||||
|
mgcosα |
|
mg cosα |
|
cosα |
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
Но |
sin α = |
h |
|
, |
|
cosα = |
1 |
− |
h2 |
|
. |
|
|||||||||||
S |
|
|
S 2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Окончательно для μ получаем выражение: |
|
|
|
|
|
|
|
|
|||||||||||||||
|
μ = |
|
|
0,1 |
|
|
|
= |
|
0,1 |
|
|
|
|
|
0,1. |
|||||||
|
|
|
1 − |
h2 |
1− |
|
|
1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
(25)2 |
|
|
|
|
|
||||||||
|
|
|
|
|
S 2 |
|
|
|
|||||||||||||||
Силу тяги выражаем из первого уравнения системы:
105

F = ma + mg Sh + 0,1mg .
F =1000 ×1 +104 × 251 + 0,1×104 = 2,4 ×103 (Н). Ответ: μ = 0,1; F = 2,4 × 103 (Н).
Аудиторные задачи
1 (уровень 1). По наклонной плоскости с углом наклона α= 30° к горизонту скользит тело. Определить скорость тела в конце второй секунды от начала скольжения, если коэффициент трения μ = 0,15. [7,26.]
2 (уровень 1). На неподвижной наклонной плоскости с углом наклона 300 лежит груз массой 5 кг, к которому привязан шнур. Конец шнура перекинут через неподвижный блок, закрепленный в вершине наклонной плоскости, и к нему подвешен груз массой 1 кг. Коэффициент трения груза о плоскость 0,2. Определите ускорение движения грузов и силу натяжения нити. [1 м/с2; 11 Н.]
3 (уровень 2). На тело массой m = 10 кг, лежащее на наклонной плоскости с углом наклона α= 20 (рис. 2.15), действует горизонтально направленная сила F = 8 H. Пренебрегая трением, определить: 1) ускорение тела; 2) силу, с которой тело давит на плоскость. [4,11 м/с2; 89,4 Н]
F
Рис. 2.15
4 (уровень 1). Найдите ту точку на прямой линии, соединяющей Землю и Луну, находясь в которой, тело будет притягиваться Луной и Землей с одинаковой силой. Расстояние между Землей и Луной считать равными 60 земным радиусам; масса Луны в 81 раз меньше массы Земли. [6 R.]
4.2.1.2 Центр масс системы материальных точек и закон его движения
Примеры решения задач
Задача 1 (уровень 1)
Плот для перевозки грузов по озеру имеет массу m = 1000 кг и длину l = 10м. Плот был неподвижным, когда одновременно навстречу друг другу двигались взрослый человек с массой m1 = 80 кг и мальчик с массой m2 = 30
кг. Определить перемещение плота в тот момент, когда взрослый пройдет весь плот, а мальчик — до середины плота.
106

Дано: |
Решение: |
|
|
||
m =1000 кг |
|
|
|
|
|
l =10 м |
|
m1 |
С |
m2 |
|
m1 = 80 кг |
|
|
|||
а) |
0 |
|
x |
||
m2 = 30 кг |
|
|
|
||
|
x |
m2 |
m1 |
||
x — ? |
|
||||
б) |
0 |
C |
x |
||
|
|||||
|
|
|
|
Рис. 2.16 |
|
Векторная сумма внешних сил, которые действуют на систему тел, состоящую из плота, взрослого человека и мальчика, равна 0. Из формулы для ускорения центра масс системы
N r arc = i∑=1Fi
N
∑mi
i=1
следует, что arñ = 0 , скорость центра масс равна 0 и положение центра масс
системы не изменяется.
Выберем ось ОХ вдоль перемещения плота с началом оси в конце плота в начальном положении (рис.2.16, а).
Координата центра масс вычисляется по формуле:
N
∑mi xi
xc = i=N1 .
∑mi
i=1
В положении а):
xñ = m10 ++m2l ++m l 2 , m1 m2 m
в положении б) после перемещения плота на х:
107
xñ = m1(l − x) + m2 (+l 2 −+x) + m( l 2 − x) . m1 m2 m
Приравнивая оба выражения для координаты центр масс, имеем:
(m1 − m2 )l
x = 2 =0,59 м m1 + m2 + m
Ответ: x = 0,59 м.
Задача 2 (уровень 2)
Определить положение центра тяжести круглой пластинки радиуса R, в
которой вырезано квадратное отверстие со стороной a = R2 так, как показано рис. 2.17.
Дано: Решение:
R |
y |
a = R2
|
x o |
|
|
|
|
x |
x — ? |
|
|
|
|
||
|
|
|
|
Рис. 2.17
Если данную в условии задачи фигуру дополнить вырезанным квадратом, то получим однородный круг, центр масс которого находится в центре круга. Выберем ось ОХ горизонтально с началом в центре круга. Предположим, что центр масс заданной пластинки расположен слева от начала координат в точке с координатой x . Тогда, используя формулу для координаты центра масс круга, можно записать:
|
m R |
+ m |
x |
||
0 = |
1 4 |
|
2 |
|
, |
m + m |
2 |
|
|||
|
|
|
|||
|
1 |
|
|
|
|
где m1 — масса вырезанного квадрата; m2 — масса пластинки с отверстием.
Отсюда:
x = − m1R . 4m2
Пусть ρ – плотность материала пластинки, h – ее толщина. Тогда
108

|
|
|
|
|
|
|
R 2 |
h = |
ρR2h |
, |
|||||
|
|
|
m = ρ |
|
|
4 |
|
|
|||||||
|
|
1 |
|
|
2 |
|
|
|
|
|
|||||
|
|
|
m2 = ρπR |
2 |
h − |
ρR2h |
= |
1 |
ρR |
2 |
h(4π −1) . |
||||
|
|
|
|
|
4 |
4 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставив m1 и m2 в формулу для x , получим |
|
||||||||||||||
|
|
|
|
|
x = − |
|
R |
|
|
. |
|
|
|
||
|
|
R |
|
4(4π −1) |
|
|
|
||||||||
Ответ: |
x = − |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||
4(4π −1) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Аудиторная задача
1 (уровень 2) Через неподвижный блок перекинута тонкая нерастяжимая нить, на концах которой подвешены грузы массами m1 = 1 кг и m2 = 2 кг. В
начальный момент времени оба груза находится на одинаковой высоте. Определить ускорение центра масс системы грузов.
[ a = (m2 −m1)2 g = 1,1 м/с2.]
(m2 +m1)2
4.2.1.3 Импульс. Закон сохранения импульса.
Примеры решения задач
Задача 1 (уровень 1)
На железнодорожной платформе, движущейся по инерции со скоростью υ0 = 3 км/ч, укреплено орудие. Масса платформы с орудием М = 10т. Ствол
орудия направлен в сторону движения платформы под углом α = 60° к гори-
зонту. Из ствола вылетает снаряд массой m = 10 кг. Определить скорость υ снаряда (относительно Земли), если после выстрела скорость платформы уменьшилась в 2 раза.
Дано: |
Решение: |
|||
υ0 = 3 км/ч |
m υ |
|||
М = 10т = 10000кг |
||||
m = 10 кг |
|
|
|
|
α = 60° |
|
|
|
|
υ = υ0 |
|
|
|
|
|
|
|
||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
Рис. 2.18 |
||
|
υ — ? |
|||
109

Импульс системы до выстрела (m + M)υ0 После выстрела система состоит из двух тел: платформы с орудием и снаряда; импульс системы:
mυr + M2υ0 .
На основании закона сохранения импульса:
(m + M )υr0 = mυr0 + M2υ0 .
Выберем ось ОХ вдоль движения платформы. Тогда проекция предыдущего равенства на эту ось дает:
(m + M )υ0 = mυcosα + M2υ0 .
Выразим искомую величину υ :
υ = mυ0 + Mυ0 2 = 835 м/с. m cosα
Ответ: 835 м/с.
Задача 2 (уровень 2)
Ракета с начальной массой М = 500 г выбрасывает непрерывную струю газов с постоянной относительно нее скоростью u = 400 м/с. Расход газов µ = 150 г/с. Пренебрегая сопротивлением воздуха и внешним силовым полем,
определить, какую скорость относительно Земли приобретет ракета через t = 2 c после начала движения, если ее начальная скорость равна нулю?
Дано: |
|
Решение: |
M = 500 г = 0,5 кг |
|
Из условия задачи следует, что внеш- |
u = 400 м/с |
|
ние силы отсутствуют. Поэтому импульс |
µ = 150 г/с = 0,15 кг/с |
|
системы тел «ракета — выбрасываемый газ» |
t = 2 c |
|
остается постоянным. Начальная скорость |
υ0 = 0 |
|
ракеты равна нулю, и вследствие этого дви- |
|
|
жение ракеты будет прямолинейным. На- |
|
|
r |
|
|
правив ось Х по скорости ракеты υ, в про- |
|
|
екции на эту ось можем записать: |
υ — ? |
(M −μt)dυ−μudt = 0 , |
|
|
||
где dυ — изменение скорости ракеты (за счет реактивного действия выбра-
сываемой струи газа) за промежуток времени dt . Отсюда
dυ = |
μu |
dt . |
|
M −μt |
|||
|
|
110
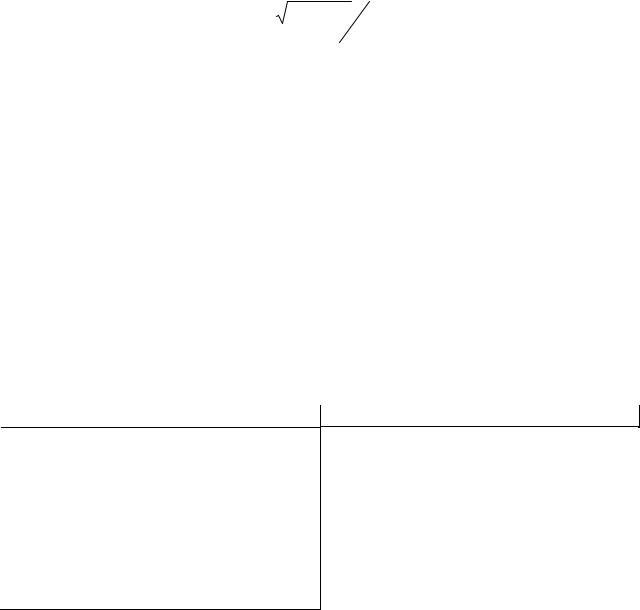
Проинтегрируем полученное выражение от 0 до t . При t = 0 υ = 0 и
t |
μdt |
|
M |
|
|
υ = u∫ |
|
= u ln |
|
. |
|
M −μt |
M −μt |
||||
0 |
|
|
Подставив численные значения, получим: υ = 366 м/с Ответ: υ = 366 м/с.
Аудиторные задачи
1 (уровень 1) С наклонной плоскости с углом наклона α к горизонту
начинает соскальзывать без трения тело массы m1 . На расстоянии l от начала движения в него попадает тело массой m2 , которое летело горизонтально. В
результате первое тело останавливается. Определить скорость второго тела до удара.
υ2 = m1 2gl sin α |
. |
|
|
|
m2 cos α. |
2 (уровень 2) Снаряд, летевший горизонтально со скоростью 12 м/с, разорвался на две части, массы которых 10 и 5 кг. Скорость большего осколка
25 м/с и направлена под углом 30° к горизонту вниз и вперед. Найти направ-
ление и величину скорости меньшего осколка. [26 м/с, 74º.]
4.2.1.4 Работа. Мощность. Кинетическая энергия
Примеры решения задач
Задача 1 (уровень 1)
Найти работу А, которую нужно выполнить, чтобы увеличить скорость дви-
жения тела массой m = 1кг от υ1 = 2 м/с до υ2 = 6 м/c на пути S = 10 м. На всём пути действует сила трения Fòð = 2 Н.
Дано:
m = 1Кг υ1 = 2м/с
υ2 = 6м/с S = 10м
Fòð = 2Н
Решение:
Для решения задачи используем
теорему о кинетической энергии:
Wk2 −Wk1 = Aâñåõ .
В процессе движения изменяется ки-
нетическая энергия тела за счёт работы А внешней силы и работы силы трения.
111

А — ?
m2υ22 − m2υ12 = A + Aòð.
Aòð = −FòðS .
Тогда:
A = m2 (υ22 − υ12 ) + FS .
A = 12 (36 − 4) + 2 ×10 = 36 (Дж).
Ответ: 36 Дж.
Задача 2 (уровень 2)
Материальная точка массой m =4 кг движется прямолинейно под действием некоторой силы так, что координата со временем меняется по закону
x = 6 +5t −t2 . Какая работа А совершается силой за первые t1 = 10 c? Какая мощность P развивается при движении точки в момент времени t2 = 5 c?
Дано: |
Решение: |
|
|
|
|
|
|
||||
m =4 кг |
По определению работы переменной силы: |
||||
x = 6 +5t −t2 |
A12 = ∫FsdS . |
|
|
||
t1 = 10 c |
|
C |
|
|
|
В нашем случае |
|
|
|
||
t2 = 5 c |
x2 |
|
|
||
A = ∫ |
FsdS . |
|
|
||
|
x1 |
|
|
|
|
A — ? |
Fx = max , |
ax = |
d 2 x |
2 |
|
|
= −2 (м/с ). |
||||
dt2 |
|||||
P — ? |
|
|
|
||
Fx = −2 ×4 = −8 (Н). |
|
|
|
||
|
|
|
|
||
x2
Работа A = ∫(−8)dx .
x1
В момент времени t2 = 10 c координата тела
x2 = 6 +5 ×10 −100 = −44 (м).
В начальный момент времени t1 = 0 координата тела
x1 = 6 (м).
Подставим полученные пределы интегрирования в формулу работы:
112

|
−44 |
|
|
|
|
||
|
A = − |
∫8dx = −8(−44 −6) |
= 400 (Дж). |
||||
|
|
6 |
|
|
|
|
|
Мощность по определению |
|
|
|
|
|||
dA |
d (Fx dx) |
|
d |
|
2 |
|
|
P = dt = |
dt |
= |
|
(−48 − 40t +8t |
|
) = −40 |
+16t = 40 (Вт). |
dt |
|
||||||
Ответ: А = 400 Дж, |
P = 40 |
Вт. |
|
|
|
|
|
Аудиторные задачи
1 (уровень 2) Груз массой m = 80кг поднимают вдоль наклонной плоскости с ускорением a = 1 м/с². Длина наклонной плоскости l = 3 м, угол α её наклона к горизонту равен 30°, а коэффициент трения µ = 0,15.
Определить: 1) работу, совершаемую подъёмным устройством; 2) его сред-
нюю мощность; 3) его максимальную мощность. [1) A = m ll (a + g sin α + µ g
cos α) = 1,72 кДж; 2) < P > = A = A a / 2l = 702Вт; 3) P |
= F at = 1,41 кВт.] |
||
|
t |
max |
|
Fr |
2 (уровень 2) Тело массой m начинает двигаться под действием силы |
||
= 2tir + 3tjr. Определить мощность P(t) , развиваемую силой в момент вре- |
|||
мени t . [Р(t) = (2t³ + 3t5 )/m.]
4.2.1.5 Потенциальная энергия. Закон сохранения механическойэнергии. Примеры решения задач.
Задача 1 (уровень 1)
На материальную точку массой m в каждой точке пространства действует
|
|
r |
= |
mB r |
|
|
|
|
|
|
|
|||
сила F |
|
x2 |
i , направленная вдоль оси x , B − константа. Доказать, что за- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
данное силовое поле консервативное. |
|
|
|
|
|
|
|
|||||||
Дано: |
|
|
|
|
Решение: |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
r |
= |
mB r |
|
|
Чтобы доказать консервативность поля, выбираем |
|
||||||||
F |
x2 |
i |
, |
|
|
|
||||||||
|
|
|
|
|
|
две произвольные точки: 1 (x , y , z ) и 2 |
(x |
|
, y |
|
, z |
|
). |
|
|
|
|
|
|
|
|
2 |
2 |
2 |
|||||
|
|
|
|
|
|
|
1 1 1 r |
|
|
|
|
|||
|
|
|
|
|
|
|
Найдём выражения для работы силы F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказать при перемещении материальной точки мас- |
|||||||
|
|
|
|
|
|
|
сой m консервативность из положения 1 в положение |
|||||||
|
|
|
|
|
|
|
2 по произвольной поля траектории: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
113
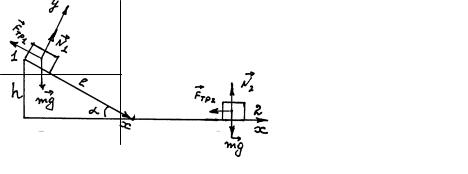
2 |
r |
r |
2 |
A12 = ∫ |
F |
dS |
= ∫F dS cosα, |
1 |
|
|
1 |
dS ×cosα = dx , так как вектор силы направлен по оси x .
2 mB |
x2 |
dx |
= |
mB |
− |
mB |
. |
|
A12 = ∫ |
x2 |
dx = mB ∫ |
x2 |
x1 |
x2 |
|||
1 |
x1 |
|
|
|
||||
Полученное выражения для A12 не зависит от конкретного вида траектории, а зависит от начальногоr и конечного положения. Следовательно, консервативность силы F доказана.
Задача 2 (уровень 2)
Тело скользит сначала с наклонной плоскости, составляющей угол α = 8° с горизонтом, а затем по горизонтальной поверхности. Найти коэффициент трения на всём пути, если известно, что тело проходит по горизон-
тальной поверхности то же расстояние, что и по наклонной плоскости.
Дано: |
Решение: |
α = 8° |
|
l= S
μ— ?
Рис. 2.19
Если на тела механической системы действуют неконсервативные си-
лы, например силы трения, то механическая энергия этой системы не остается постоянной. Изменение механической энергии такой системы равно сум-
марной работе всех неконсервативных сил. В данной задаче на движущееся
тело действуют следующие силы: сила тяжести — консервативная; сила ре-
акции опоры; работа по перемещению тела (равна 0, так как эта сила перпен-
дикулярна перемещению); сила трения — неконсервативная. Рассмотрим те-
ло в двух положениях: (1) в начале движения на вершине наклонной плоско-
сти и (2) — в конце движения на горизонтальном участке.
Потенциальную энергию будем отсчитывать от основания наклонной
плоскости. Тогда по закону изменения механической энергии можно записать:
(Wk2 +Wn2 )− (Wk1 +Wn1 )= Aòð1 + Aòð2
где Aòð1 − работа силы трения при движении тела по наклонной плоскости; Aòð2 − работа силы трения на горизонтальном участке пути;
114
Wk1 Wn1 Wk2 Wn2
Aòð1
=0 , так как в верхней точке тело покоится;
=mgh ;
=0, так как тело остановилось;
=0 , так как h = 0;
=Fòð S cosπ = −FòðS .
Сила трения Fòð = μN , где N — сила реакции опоры.
На наклонной плоскости проекция уравнения движения тела (второго закона Ньютона) на ось OY дает:
|
N1 − mg cosα = 0 , |
Откуда |
N1 = mg cosα, |
|
Fòð = μmg cosα. |
|
1 |
На горизонтальном участке пути:
N2 − mg = 0 .
Тогда для работ сил трения получим:
= −μmgcosαl ,
= −μmgS .
Подставляем полученные слагаемые в закон изменения механической
энергии:
(0 + 0) − (0 + mgh) = −μmg cos α×l −μmg × S .
Cократим на mg и учтём, что l = S = |
|
|
|
h |
. Получим: |
||||||
sin α |
|||||||||||
|
|
h |
|
h |
|
||||||
−μcosα |
|
|
|
−μ |
|
|
= −h , |
||||
sin α |
|
sin α |
|||||||||
|
|
|
|
|
|||||||
откуда выражаем коэффициент трения |
|
|
|
|
|
||||||
μ = |
|
1 |
|
|
|
|
|
= 0,07. |
|||
ctgα + |
|
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
||||
|
sin α |
|
|||||||||
|
|
|
|
|
|||||||
Ответ: 0,07.
Аудиторные задачи
1 (уровень1) Потенциальная энергия частицы в силовом поле изменяется по закону Wï = 2x2 + 3y2 + 0,5z . Найти работу, совершаемую над частицей силами поля при переходе из точки с координатами x1 = 0,5 м, y1= = 1 м,
z1 = 0,2 м в точку с координатами x2 = 0,1 м, y2 = 0,75 м, z2 =0,1м.
115

Найти выражение для силы, действующей на частицу и величину этой силы в начальной и конечной точках. [А = 1,8425 Дж; F=-(4xi +6yjr+0,5kr);
F1 = 6,34 Н, F2 = 4,545 Н.]
2 (уровень 2) Тело массой m = 200 г, брошенное под углом α =60° к горизонту, упало на расстоянии S = 10 м от места бросания через t = 20 с.
Не учитывая сопротивления воздуха, определить работу, затраченную во время броска; кинетическую и потенциальную энергию тела в верхней точке траектории [А = 10 Дж; Wк=2,5 Дж; Wр= 7,5 Дж.]
4.3. МАТЕРИАЛЫ К ЛАБОРАТОРНЫМ ЗАНЯТИЯМ
4.3.1 Лабораторная работа «Определение коэффициента трения
при скольжении тела по наклонной плоскости»
Основные понятия, определения и формулы динамики поступательного движения абсолютно твердого тела
1.Первый закон Ньютона. Существуют такие системы отсчета, относительно которых тело движется равномерно и прямолинейно, если на него не действуют другие тела или действие других тел скомпенсировано. Такие системы отсчета называются инерциальными системами отсчета.
2.Масса тела — мера его инертности, т. е. способности тела сохранять свою скорость постоянной. Сила — векторная физическая величина, описывающая механическое действие тел друг на друга.
3.Второй закон Ньютона. Ускорение, с которым тело поступательно движется, прямо пропорционально векторной сумме действующих на тело
сил и обратно пропорционально массе тела:
N r
ar = i∑=1Fi . m
4. Закон динамики поступательного движения тела:
r N r ma = ∑Fi .
i=1
5.Третий закон Ньютона. Тела взаимодействуют друг с другом с силами, равными по величине и противоположными по направлению.
Если тела представляют собой материальные точки, то эти силы взаимодей-
ствия направлены по прямой, их соединяющей.
6.Величина массы тела равна отношению модуля ускорения эталона массы к модулю ускорения тела, причем масса эталона принимается за еди-
ницу массы:
m = aaýò mýò , mýò =1 (массы).
116

Вединицах СИ mýò =1 кг.
7.Коэффициентом трения μ при скольжении одного тела по поверх-
ностиr другого называется величина, равная отношению модуля силы трения
Fòð к модулю силы реакции опоры N , действующих на движущееся тело:
μ = FNòð .
При скольжении тела сила трения направлена против вектора скорости.
8.Весом тела называется сила, с которой тело действует на опору или
подвес.
9.Импульсом тела p называется физическая величина, равная произ-
ведению массы тела на его скорость:
p= mυ.
10.Импульсом системы N тел называется векторная сумма импульсов всех тел, входящих в систему:
Pr = ∑N pr.
i=1
11.Замкнутой системой тел называется система, на которую не дей-
ствуют силы со стороны тел, не входящих в систему (внешние силы).
12. Закон сохранения импульса. Импульс замкнутой системы посту-
пательно движущихся тел остается постоянным:
P= const .
13.Импульсом силы называется произведение вектора силы на про-
межуток времени ее действия.
14. Изменение импульса системы тел за промежуток времени t
равно векторной сумме импульсов внешних сил, действующих на тела системы:
P = ∑Fi t .
ir
15.В механике элементарной работой δA силы F над телом, совер-
шающим бесконечно малое перемещение dr , называется величина, равная
скалярному произведению векторов F и dr :
δA = F drr = F dr cosα = FdScosα.
16. Кинетической энергией тела Wk |
называется физическая величина, |
|||
изменение которой равно алгебраической сумме работ всех N сил, дейст- |
||||
вующих на тело: |
|
|
|
2 |
|
N |
W = mυ |
||
W = ∑A , |
. |
|||
k |
i=1 i |
k |
2 |
|
Кинетическая энергия есть количественная мера способности движущегося тела совершать работу.
117
17. Сила, работа которой при перемещении тела из начальной точки в конечную, не зависит от формы траектории, соединяющей эти точки, называ-
ется консервативной силой.
18. Потенциальной энергией тела Wï называется физическая вели-
чина, изменение которой, взятое со знаком « − », равно работе действующей на него консервативной силы:
− Wï = Aêîí .
Потенциальная энергия есть количественная мера способности тела, находящегося под действием консервативных сил, совершать работу.
19. Между консервативной силой Fêîí , действующей на тело, и его по-
тенциальной энергией существуетr связь:
Fêîí = −gradWï .
20.Механической (полной механической) энергией тела называется
алгебраическая сумма кинетической и потенциальной энергий тела.
21.Механической (полной механической) энергией системы тел называется алгебраическая сумма механических энергий всех N тел, входящих в систему:
N
Wìåõ = ∑(Wki +Wï i ) .
i=1
22. Закон сохранения механической энергии. Полная механическая энергия системы тел, на каждое из которых действуют только консервативные силы, постоянна:
Wìåõ = const .
23. Изменение полной механической энергии системы тел равно алгеб-
раической сумме работ всех неконсервативных N сил, действующих на тела системы:
N
Wìåõ = ∑Aíåê i . i=1
Описание лабораторной установки и хода выполнения лабораторной работы
Коэффициент трения можно определить, рассматривая движение тела по
наклонной плоскости (рис. 2.20). Если тело положить на наклонную плоскость,
то оно под действием силы тяжести придет в движение с постояннымrускоре- |
|
нием. В самом деле, на тело действует сила тяжести mg , сила трения Fòð , сила |
|
реакции опоры Nr . Применяя второй закон Ньютона, можем записать: |
|
mgr + N + Fòð = mar. |
(1) |
y
118
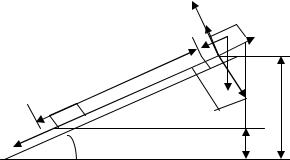
N |
Fтр |
l |
|
mg |
h1 |
x α |
h2 |
Рис. 2.20
Так как каждую из этих сил можно считать постоянной, то и сумма векторов этих сил будет постоянной. Следовательно, и ускорение также бу-
дет постоянным. |
|
|
|
Уравнение движения (1) в проекции на оси OX,OÓ примет вид: |
|
||
mg sin α − Fòð = ma , |
(2) |
||
− mg cosα + N = 0 . |
(3) |
||
Модуль силы трения через коэффициент трения μ математически вы- |
|||
ражается так: |
|
|
|
Fòð = μN , |
|
|
|
где N — модуль силы реакции опоры. Тогда из равенства (3) получим: |
|
||
Fòð = μmg cosα. |
(4) |
||
С учетом соотношения (4) выражение (2) примет вид: |
|
||
mg sin α−μmg cosα = ma , |
|
||
или |
|
|
|
g sin α−μg cosα = a . |
(5) |
||
Если cosα ≠ 0 (т.е. α ≠ π ), получим равенство |
|
||
2 |
a |
|
|
g(tgα −μ) = |
. |
|
|
cosα |
|
||
|
|
|
|
Из последнего соотношения видно, что существует такой минимальный угол наклона плоскости к горизонту ( α = αmin ), при котором тело будет скользить
с постоянной скоростью ( a = 0 ). В этом случае будет выполняться равенство: g(tgαmin −μ) = 0 ,
из которого определяем: |
|
μ = tgαmin . |
(6) |
Однако найденное по формуле (6) значение μ будет весьма прибли-
женным, так как экспериментально трудно с высокой точностью определить величину αmin . Для более точного определения коэффициента трения можно
поступить следующим образом. Если установить угол α несколько больший,
чем αmin ( α = α1), то тело будет скользить с ускорением. Пусть за время |
t1 |
|||
от начала движения оно пройдет путь l . Тогда |
|
|||
|
at2 |
|
||
l = |
1 |
, |
(7) |
|
2 |
||||
|
|
|
||
119

откуда: |
2l |
|
|
|
|
|
a = |
, |
|
|
|
||
t2 |
|
|
|
|||
|
|
|
|
|
||
и равенство (5) примет вид: |
1 |
|
|
|
|
|
|
|
2l |
|
|
||
g sin α −μg cosα = |
. |
(8) |
||||
|
||||||
1 |
|
1 |
t2 |
|
||
|
|
|
1 |
|
|
|
Из этого выражения можно определить величину коэффициента трения:
μ = tgα1 − |
|
2l |
|
|
|
|
. |
(9) |
|
gt2 |
cosα |
|||
1 |
1 |
|
|
|
Для уменьшения возможной систематической ошибки в определении
угла α, а значит и величины μ, измерения можно провести при двух значениях угла α.
Увеличив угол наклона плоскости от значения α1 до значения α2 , и измерив временя прохождения того же пути l , получим значение t2 < t1. При
этом будет справедливо следующее соотношение:
g sin α2 −μg cosα2 = 22l . (10) t2
Умножив обе части равенств (8) и (10) соответственно на sin α2 и sin α1 а затем вычтя из первого второе, получим:
|
|
|
|
|
sin α |
|
sin α |
2 |
|
|
μg(sin α |
|
cosα −cosα |
|
sin α ) = 2l |
1 |
− |
|
. |
||
|
|
t2 |
t2 |
|
||||||
|
2 |
1 |
2 |
1 |
|
|
|
|
||
|
|
|
|
|
|
2 |
|
1 |
|
|
Из последнего равенства выражаем коэффициент трения:
|
sin α |
|
|
sin α |
2 |
|
|
||
|
|
1 |
− |
|
|
|
|||
|
t2 |
t2 |
|
|
|||||
|
2l |
|
|
|
|||||
μ = |
|
2 |
|
|
1 |
|
|
. |
(11) |
g sin(α |
2 |
−α ) |
|
||||||
|
|
|
|
||||||
|
|
|
|
1 |
|
|
|
|
|
Для определения μ по формулам (9) или (11) необходимо знать рас-
стояние l , проходимое телом за измеряемый промежуток времени. Если оно одинаково при обоих значениях угла, то его можно не измерять. Разделив (8) на (10), получим выражение:
sin α |
−μ cosα |
t2 |
|
|
1 |
1 |
= |
2 |
, |
sin α2 |
|
t12 |
||
−μ cosα2 |
|
|||
из которого получается еще одна формула для коэффициента трения:
|
t2 |
sin α −t2 |
sin α |
2 |
|
|
||
μ = |
1 |
1 |
2 |
|
. |
(12) |
||
t2 |
cos α −t2 |
|
|
|||||
|
cos α |
2 |
|
|
||||
|
1 |
1 |
2 |
|
|
|
|
|
Рабочую формулу (9) (следовательно, и (11), (12)) можно получить изравенства, выражающего изменение механической энергии движущегося по наклонной плоскости тела.
120

Пусть рассматриваемая система тел состоит из одного тела − тела, движущегося по наклонной плоскости. При его движении отличную от нуля
механическую работу совершают только сила тяжести mgr и сила трения Fòð ,
причем сила трения — неконсервативная сила. Поэтому можно записать: |
|
Wï 2 +Wk 2 −(Wï 1 −Wk1 ) = Aòð . |
(13) |
Если за нулевой уровень потенциальной энергии принять горизонтальную плоскость, проходящую через основание наклонной плоскости, то
Wk1 = 0 , |
|
Wï1 |
= mgh1 , |
||
W |
= |
mυ2 |
, |
W |
= mgh , |
|
|||||
k2 |
2 |
|
ï2 |
2 |
|
|
|
|
|
||
Aòð = −Fòðl .
Подставляя эти выражения в равенство (13), получим:
mg(h |
− h ) + |
mυ2 |
= −F l . |
(14) |
|
||||
2 |
1 |
2 |
òð |
|
|
|
|
|
|
Учитывая соотношение (4) а также очевидные равенства: |
|
|||
υ = at , |
|
h2 −h1 = −l sin α, |
|
|
вместо выражения (14) можно записать;
−mgl sin α+ ma2t2 = −μmg cosα l . 2
С учетом выражения (7) из этого последнего равенства вытекает формула (9).
Рабочую формулу (9) можно получить, рассматривая изменение импульса движущегося тела. Действительно, на основании утверждения, сформулированного в п. 3.2.1.1 «Законы динамики материальной точки», формула 2.9, можно записать следующее:
|
|
|
r |
r |
r |
|
но |
υ1 = 0 , |
r |
rmυ2 |
− mυ1 |
= Fòðt + mgt + Nt , |
|
υ2 |
= υ = at ; поэтому получаем: |
|
||||
|
|
|
mart = Fòðt + mgrt + Nt . |
(15) |
||
В проекции на ось OX равенство (15) примет вид: |
|
|||||
|
|
|
mat |
= − Fòð t + mg sin α t , |
|
|
или, учитывая равенства (4) и (7),
m 2tl = −μmg cosα t + mg sin α t .
Выражая из последнего равенства коэффициент трения μ , приходим к рабочей формуле (9).
Задания
I уровень
121
1. Измерить угол наклона наклонной плоскости αmin 5 раз. По результатам измерений определить коэффициент трения μ по формуле (6) для каждого опыта. Найти среднее значение μñð , среднюю абсолютную и относительную ошибки. Данные измерений и результатов вычислений занести в табл. 2.1.
2. Установить угол наклона плоскости α > αmin . Наблюдать ускоренное дви-
жение тела по плоскости и измерить путь, проходимый телом, l и время движения t . Измерения проводить 5 раз при неизменном значении l . Для каждого опыта вычислить коэффициент трения по формуле (9), найти среднее значение μñð , среднюю абсолютную и относительную ошибки. Резуль-
таты измерений и вычислений занести в табл. 2.2.
|
|
|
|
|
Таблица 2.1 |
||
№ опыта |
αmin |
μ |
μ |
|
μñð |
100 % |
|
μñð |
|||||||
|
|
|
|
|
|
||
1. |
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
Среднее |
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.2 |
||
№ опыта |
l = |
|
α = |
|
μñð |
100 % |
|
t |
μ |
μ |
|
||||
|
μñð |
||||||
|
|
|
|||||
1. |
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
Среднее |
|
|
|
|
|
|
|
IIуровень
1.Измерить угол наклона наклонной плоскости αmin 5 раз. По результатам
измерения определить коэффициент трения μ по формуле (6) для каждого опыта. Найти среднее значение μñð, среднюю абсолютную и относительную
ошибки. Данные измерений и результатов вычислений занести в табл. 2.1. 2. При двух различных углах наклона плоскости α1 > αmin и α2 > αmin изме-
рить время движения тела по наклонной плоскости t1 и t2 соответственно (по
5 раз каждое из этих времен). Измерить также одинаковое для всех опытов расстояние l . Вычислить коэффициент трения по формулам (11) или (12). Рассчитать среднее значение этой величины, среднюю абсолютную и относительную ошибки. Результаты измерений и вычислений записать в табл. 2.3.
3. Вычислить вес тела, движущегося по наклонной плоскости.
122
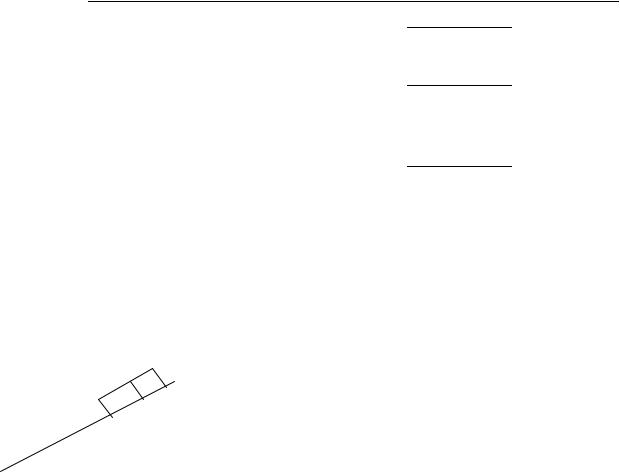
|
|
l = |
|
|
|
Таблица 3 |
|||
|
|
α1 = |
|
α2 = |
|||||
№ опыта |
t |
|
t2 |
μ |
μ |
|
|
μñð |
|
|
|
|
|
μñð |
|||||
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
|
|
Среднее |
|
|
|
|
|
|
|
|
|
III уровень
1.Для каждого из двух брусков с массами m1 и m2 , которые имеют различные коэффициенты трения μ1 и μ2 соответственно, определить эти коэффициенты, проводя измерения пункта 2 задания I уровня. С каждым бруском проводить измерения 3 раза и найти таким образом μ1ñð и μ2ñð .
m2 |
2. Положить на наклонную плоскость оба со- |
||||
прикасающихся |
бруска, |
причем, |
брусок, |
||
m1 |
|||||
имеющий больший коэффициент трения, дол- |
|||||
|
|||||
|
жен на наклонной плоскости лежать ниже дру- |
||||
|
гого бруска. На |
рис. 2.21 показан случай |
|||
|
μ1> μ2 . Измерить |
время |
движения |
соприка- |
|
|
|||||
|
сающихся брусков t , длину пути l и из форму- |
||||
Рис 2.21 |
лы (7) найти ускорение грузов aýêñ. |
|
|||
3. Теоретически рассмотреть задачу: два соприкасающихся бруска с известными массами и коэффициентами трения движутся по наклонной плоскости, имеющей известный угол наклона к горизонтали. Вывести формулу для ускорения брусков. По полученной формуле вычислить теоретическое значение ускорения брусков aòåîð . Сравнить aýêñ и aòåîð .
4. Решая далее указанную задачу, вывести формулу для силы взаимодействия брусков и вычислить эту силу.
4.3.2 КОНТРОЛЬНЫЕ ЗАДАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ
4.3.2.1 Вопросы предварительного контроля (компьютерный допуск к лабораторной работе)
Законы Ньютона. Импульс
1. Тело под действием двух сил движется равномерно и прямолинейно. Величина одной из сил равна 6 Н. Чему равна величина второй силы?
123
2. На тело действует постоянная сила, величина которой 2 Н. Как движется тело, если сила направлена в сторону начальной скорости?
1)Равномерно;
2)покоится;
3)равноускоренно;
4)равнозамедленно.
3. Тело массой 10 кг движется по оси X по закону x = 3t3 + 2t +1) м. Вычислить величину равнодействующей силы в момент времени 2 с.
4.Мяч массой 2 кг падает вертикально вниз на пол и перед ударом имеет скорость 10 м/с. Он отскакивает с той же по величине и противоположной по направлению скоростью. Вычислить импульс силы, действующей на мяч при ударе.
5.При взаимодействии двух шаров с массами 0,2 кг и 0,4 кг первый шар получил ускорение 10 м/с2. Какое ускорение получил второй шар?
6.Два шара с массами 0,2 кг и 0,3 кг движутся навстречу друг другу со скоростями 6 м/с и 4 м/с соответственно. С какой скоростью движутся эти шары после абсолютно неупругого удара?
7.На тело массой 5 кг действуют две взаимно перпендикулярные силы, величина одной из них равна 3 Н, второй — 4 Н. С каким ускорением движется тело?
Механическая работа. Кинетическая энергия
1.Санки массой 5 кг равномерно тянут за веревку со скоростью 4 м/c по горизонтальной дороге. Сила натяжения веревки равна 100 Н и направлена под углом 60º к горизонтали. Вычислить работу силы натяжения за промежуток времени 2 с.
2.Санки массой 5 кг равномерно тянут за веревку со скоростью 4 м/c по горизонтальной дороге. Сила натяжения веревки равна 100 Н и направлена под углом 60º к горизонтали. Вычислить работу силы трения, действующей на санки.
3.Коэффициент жесткости пружины, имеющей длину 0,2 м, равен 50 Н/м. Какую работу надо выполнить, чтобы растянуть пружину до длины 3 м.
4.Тело массой 1 кг свободно падает с высоты 5 м. На него действует постоянная сила сопротивления 4 Н. Вычислить кинетическую энергию тела
впоследней точке движения. Ускорение свободного падения принять равным
10 м/c2.
5.Тело движется равномерно под действием двух сил. Работа одной из них за определенный промежуток времени равна 200 Дж. Каково численное значение работы второй силы?
6.Тело массой 1 кг движется по наклонной плоскости, образующей
угол 30º с горизонталью. Вычислить работу силы тяжести тела на пути 20 м. Ускорение свободного падения принять равным 10 м/c2.
124
7. На толкание ядра массой 2 кг затрачена работа 400 Дж. С какой начальной скоростью полетит ядро?
Потенциальная энергия. Закон сохранения механической энергии
1.Какие из перечисленных ниже сил являются консервативными?
1)сила тяжести
2)сила трения
3)сила упругости
4)сила тяги
5)сила сопротивления
6)центробежная сила
7)сила всемирного тяготения
2.Упругая пружина в недеформированном состоянии имеет длину 0,2 м. Сначала она была растянута до длины 0,25 м, а затем — до 0,3 м. Во сколько раз потенциальная энергия пружины после второго растяжения больше, чем после первого?
3.Тело массы 1 кг брошено горизонтально с начальной скоростью 2 м/c на высоте 6 м. Найти полную механическую энергию тела через 1 секунду после начала движения.
4.В левом столбике записаны выражения потенциальных энергий в случаях действия на тело некоторых консервативных сил. В правом столбике
−названия консервативных сил. Для каждой строки левого столбика найти соответствующую строку правого столбика.
1) G mM |
1) сила тяжести |
||
|
r |
|
|
2) |
kx2 |
2) сила упругости |
|
2 |
|
||
|
|
|
|
3)mgh 3) сила всемирного притяжения
5.Тело массой 1 кг брошено с поверхности земли с начальной скоростью 3 м/с, составляющей угол 45º с горизонтом. Чему равна механическая энергия тела через 0,1 с после начала движения? Сопротивление воздуха не учитывать.
6.Два тела — Земля и Луна — взаимодействуют друг с другом по закону всемирного тяготения. Каждое из них по этому же закону взаимодействует с солнцем. Выполняется ли для системы двух тел Земля-Луна закон сохранения механической энергии?
7.Тело массы 0,2 кг скользит по наклонной плоскости, начиная с высоты 1 м над горизонтальной поверхностью. Чему равна работа силы трения, если скорость тела у подножья наклонной плоскости равна 4 м/с?
Вопросы по выполнению лабораторной работы
125
1.Тело массой m двигается по наклонной плоскости с углом наклона α к горизонту при коэффициенте трения μ. Какова связь между величинами α
иμ при равномерном движении тела?
2.Тело массой m движется по наклонной плоскости равноускоренно. Какие из перечисленных ниже величин измеряются в данной лабораторной работе?
1)m , 2) h , 3) t1, 4) υ, 5) a — ускорение, 6) α — угол наклона плос-
кости, 7) F — сила трения.
3. Тело движется по наклонной плоскости равноускоренно. Какие из приведенных ниже величин необходимо вычислить в данной лабораторной работе?
1) m , 2) h , 3) t1, 4) υ, 5) a — ускорение, 6) α — угол наклона плоскости, 7) μ — коэффициент трения, 8) F — сила трения.
4.Тело движется по наклонной плоскости равномерно. Выполняется ли для него закон сохранения механической энергии?
5.Тело массы m движется по наклонной плоскости с углом наклона к горизонту α. При этом коэффициент трения между плоскостью и телом μ.
Записать величину силы трения, действующей на тело.
6. При движении тела по наклонной плоскости его импульс изменяется от значения mυ1 до значения mυ2 . Изменение импульса тела равно:
1)работе силы трения;
2)работе силы тяжести;
3)сумме импульсов сил, действующих на тело;
4)сумме сил, действующих на тело;
5)изменению кинетической энергии тела.
4.3.2.2.Контрольные вопросы для защиты лабораторной работы
Iуровень
1.Дать формулировки законов Ньютона и записать уравнение поступательного движения тела, т.е. второй закон Ньютона.
2.Рассмотреть поступательное движение тела по наклонной плоскости
сучетом силы трения. Получить формулу (9) для коэффициента трения.
3.Какой угол наклона плоскости называется минимальным? Получить формулу (6), связывающую минимальный угол наклона плоскости с коэффициентом трения.
4.Сформулировать закон сохранения импульса и закон сохранения механической энергии.
126
IIуровень
1.Рассматривая поступательное движение тела по наклонной плоскости при двух различных углах ее наклона к горизонту, получить из второго закона Ньютона расчетные формулы (11) и (12).
2.Какие силы называются консервативными? Являются ли консервативными силы, действующие на движущееся по наклонной плоскости тело?
2.Применяя закон изменения механической энергии, получить формулу (9) для вычисления коэффициента трения.
3.Применяя закон изменения импульса, получить формулу (9) для вычисления коэффициента трения.
127
IIIуровень
1.Рассмотреть движение по наклонной плоскости двух соприкасающихся тел, имеющих различный коэффициент трения. Считать, что коэффициент трения тела, находящегося ниже на плоскости, больше, чем второго тела. Для этого случая из законов Ньютона получить аналитические выражения для ускорения тел, а также для силы взаимодействия между ними.
2.Проанализировать полученные в предыдущем пункте формулы для случаев μ1 > μ2 , μ1 = μ2 , μ1 < μ2 .
3.Рассмотреть движение по наклонной плоскости двух соприкасаю-
щихся тел, имеющих различные коэффициенты трения, исходя из закона изменения механической энергии. Получить выражение для ускорения тел в этом случае.
4.4 МАТЕРИАЛЫ ДЛЯ УПРАВЛЯЕМОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
Задание № 1
Доказать и письменно изложить консервативность силы тяжести и силы упругости.
Задание № 2
Изучить теорию применения законов сохранения импульса и механической энергии к абсолютно упругому и абсолютно неупругому ударам (законспектировать). Ознакомиться со следующими примерами решения задач по этой теме.
Примеры решения задач
Задача 1. Тело массой m1 ударяется абсолютно неупруго о тело массой m2 Найти долю q потерянной при этом кинетической энергии, если тело m2
до удара было в покое.
Решение. Доля потерянной кинетической энергии
q = |
Wk1 −Wk 2 |
, |
(1) |
|
W |
||||
|
|
|
||
|
k |
|
|
|
1 |
|
|
||
где Wk1 ,Wk2 — кинетическая энергия системы соответственно до и после соударения:
W |
|
= |
m1υ12 |
|
|
(m + m |
)u2 |
|
k1 |
|
, W |
= |
1 2 |
|
(2) |
||
|
||||||||
|
|
|
||||||
|
|
2 |
k2 |
|
2 |
|
|
|
υ — скорость первого тела до удара; u — скорость тел после абсолютно неупругого удара; применив закон сохранения импульса, найдем:
u = m1υ1 /(m1 + m2 ) |
(3) |
128

Подставив значения (2) и (3) в формулу (1), получим:
q = m2 /(m1 + m2 ).
Эта доля кинетической энергии перешла во внутреннюю энергию соударяющихся тел.
Задача 2. Два свинцовых шара массами m1 = 2 кг и m2 = 3кг подвешены на нитях длиной l = 70 см. Первоначально шары соприкасаются между собой, затем меньший шар отклонили на угол α = 60о и отпустили. Считая удар центральным и неупругим, определить: 1) высоту h , на которую поднимутся шары после удара; 2) энергию W , израсходованную не деформацию шаров при ударе.
Решение. Удар неупругий, поэтому после удара шары движутся с общей скоростью υ, которую найдем из закона сохранения импульса:
m1υ1 + m2υ2 = (m1 + m2 )υ. |
(1) |
где υ1, υ2 — скорости шаров до удара. Скорость υ1 малого шара найдем из закона сохранения механической энергии:
m1gh1 = m1υ12 / 2 ,
откуда
υ1 =  2gh1 =
2gh1 =  2gl(1 − cos α) = 2
2gl(1 − cos α) = 2 gl sin(α/ 2) (учли, что h1 = l(1 −cosα)).
gl sin(α/ 2) (учли, что h1 = l(1 −cosα)).
Из выражений (1) и (2), при условии, что υ1 = 0, получим:
|
|
υ m |
|
|
|
|
|
2m |
gl sin(α ) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
||||||||
υ = |
|
|
1 |
|
1 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||
|
m |
+ m |
|
|
m + m |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
||||
Из закона сохранения механической энергии имеем: |
|||||||||||||||||||||||||||
|
|
(m + m |
|
) |
υ2 |
= (m + m |
|
|
)gh, |
||||||||||||||||||
|
|
|
2 |
|
|
||||||||||||||||||||||
откуда искомая высота |
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ |
2 |
|
|
|
2m2l sin2 (α |
2 |
) |
|
|
|
|
|
|||||||||||
|
|
h = |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
g = |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(учли формулу (3)). |
|
|
|
|
|
(m1 +m2 )2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Энергия, израсходованная на деформацию шара при ударе, |
|||||||||||||||||||||||||||
|
|
|
|
|
|
m υ2 |
|
|
(m |
+m |
2 |
)υ2 |
|
|
|
|
|||||||||||
|
|
W = |
|
|
1 |
|
1 |
|
− |
|
1 |
|
|
|
|
|
|
|
|
, |
|
||||||
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
или, подставив (2) в (4), получим: |
|
m1m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
W = 2gl |
|
|
sin2 (α |
2 |
) . |
|||||||||||||||||||||
|
m1 + m2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(2)
(3)
(4)
Вычисляя, получим: 1) h = 5,6 см; 2) W = 4,12 Дж.
Задача 3. Пять одинаковых шаров, центры которых лежат на одной прямой, находятся на небольшом расстоянии друг от друга. С крайним
129
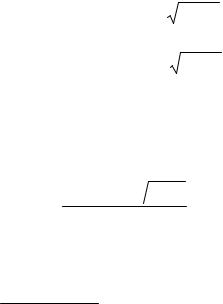
шаром соударяется такой же шар, имеющий скорость υ = 10 м/с и движущийся вдоль прямой, соединяющей центры шаров. Найти скорость последнего шара, считая соударения шаров абсолютно упругими.
Решение. При абсолютно упругом соударении двух одинаковых шаров происходит обмен скоростями. Движущийся шар останавливается, а покоящийся приобретает его скорость. Это непосредственно вытекает из выражений для скоростей шаров после соударения:
υ1′ = |
(m1 − m2 )υ1 + 2m2υ2 ; |
υ′2 |
= |
(m2 − m1)υ2 + 2m1υ2 ; |
|
m1 + m2 |
|
|
m1 + m2 |
При m1 = m2 |
и υ2 = 0 будем иметь |
υ′2 = 0, υ′2 = υ1. Поэтому после ряда |
||
последовательных соударений все шары будут покоиться, кроме последнего шара, который приобретает скорость υ = 10 м/с.
Задача 4. Два шарика массы m1 и m2 одновременно начинают соскаль-
зывать навстречу друг другу без трения и вращения с двух горок одинаковой формы и высоты Н. При столкновении шарики слипаются. На какую высоту поднимутся слипшиеся шарики?
Решение. По условию задачи удар абсолютно неупругий. В верхних точках наклонных плоскостей скорости тел равны нулю. Их потенциальная энергия переходит в кинетическую у основания:
|
|
m υ2 |
|
|
|
m gH = |
1 |
|
|
υ = 2gH. |
|
|
|
|
|||
1 |
2 |
|
|
||
|
|
|
|||
|
|
m |
υ2 |
|
|
m2 gH = |
|
2 |
|
|
υ = 2gH. |
2 |
|
||||
|
|
|
|||
Как видно, скорости тел до удара равны. Запишем закон сохранения импульса в проекции на горизонтальную ось X:
m1υcosα − m2υcosα = (m1 + m2 )u cosα.
Сократим на cos α и получим выражение для υu :
u = (m1 −m2 ) 2gH . m1 + m2
2gH . m1 + m2
Далее кинетическая энергия уже системы тел переходит в потенциальную на высоте h :
(m1 + m2 )u2 = (m1 + m2 )gh; 2
из этого равенства выражаем h , учитывая выражение для u :
|
u2 |
|
(m −m |
)2 2gH |
|
||
h = |
|
= |
1 2 |
|
|
; |
|
2g |
(m1 + m2 )2 |
2g |
|||||
|
|
|
|||||
130

h= m1 −m2 2 H.
m1 + m2
|
|
−m2 |
2 |
|
|
Ответ: |
|
m1 |
|
H. |
|
|
+ m |
||||
h = m |
|
||||
|
1 |
2 |
|
|
|
Задание №3
Решить задачи индивидуального задания по теме «Динамика материальной точки и поступательного движения твердого тела. Работа и энергия» из следующего ряда задач.
1 Законы Ньютона
Уровень 1
1.1Стальная проволока некоторого диаметра выдерживает силу натяжения 4,4 кН. С каким наибольшим ускорением а можно поднимать груз мас-
сой 400 кг, подвешенный на этой проволоке, чтобы она не разрывалась? [1,25 м/с2.]
1.2Поезд массой 500 т, двигаясь равнозамедленно, в течение 1 мин уменьшает свою скорость от 40 км/ч до 28 км/ч. Найти силу торможения F. [27,7 кН.]
1.3 Тело массой m движется в плоскости ХY |
по закону |
x = Acosωt, y = Bsinωt (A, B и ω положительные постоянные). |
Определить |
модуль силы, действующей на это тело. [F = mω2 A2 + B2 .] |
|
1.4. На коляске, которая движется в горизонтальном направлении с ускорением a = 9,8 м/с2, установлен подвес. Найти натяжение нити отвеса и угол, который образует нить с вертикалью. Масса груза m = 0,1 кг.
[F = m a2 + g 2 =1,4 H, 45°.]
a2 + g 2 =1,4 H, 45°.]
1.5. Определить коэффициент трения между наклонной плоскостью и телом, которое движется по ней, если известно, что тело имеет начальную скорость υ0 = 5 м/с и за время движения вверх проходит путь S = 2м. Угол на-
клона плоскости |
α= 300. |
μ = (υ02 |
− 2Sg sin α) |
2Sg cosα |
= 0,16. |
|
|
|
|
|
|
|
|
|
|
|
|
Уровень 2.
a.На рис. 2.22 изображена система блоков, к которым подвешены грузы
131
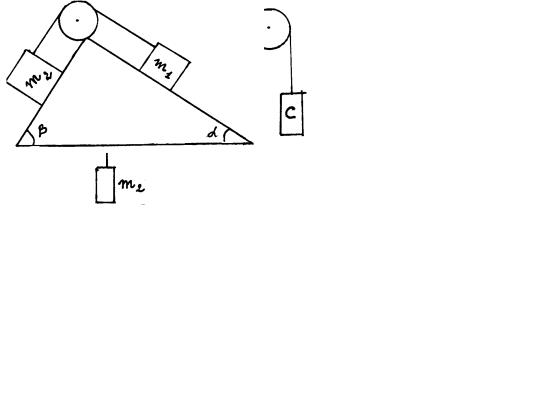
массами m1 = 200 г и m2 = 500 г. Считая, что груз m1 поднимается, а блок с m2 опускается, нить и блоки невесомы, силы трения отсутствуют, опреде-
лить: 1) силу натяжения нити Т; 2) ускорения, с которыми движутся грузы. [1) 2,26 Н; 2) a1 = 1,5 м/с2, a2 = 0,75 м/с2.]
Рис. 2.22 |
Рис. 2.23 |
Рис 2.24
1.7. Тело А массой M = 2 кг (рис. 2.23) находится на горизонтальном столе и соединено нитями посредством блоков с телами В ( m1 = 0,5 кг) и С (m2 = 0,3 кг).
Считая нити и блоки невесомыми и пренебрегая силами трения, определить: 1) ускорение, с которым будут двигаться эти тела; 2) разность сил натяжения нитей. [1) 0,78 м/с2; 2) 1,33 Н.] 1.8 В установке (рис. 2.24) углы α и β с горизонтом соответственно равны
30° и 45°, массы тел m1 = 0,45 кг и m2 = 0,5 кг. Считая нить и блок невесомы-
ми и пренебрегая силами трения, определить: 1) ускорение, с которым движутся тела; 2) силу натяжения нити. [1) 1,33 м/с2; 2) 2,8 Н.]
1.9. Система грузов массами m1 = 0,5 кг и m2 = 0,6 кг находится в лифте,
движущемся вверх с ускорением a = 4,9 м/с2 (рис. 2.25). Определить силу натяжения нити, если коэффициент трения между грузом массой m1 и опорой
μ = 0,1.
[T = |
m1m2 |
(1+μ)(a + g) = 4,41 Н.] |
|
|
|||
|
m + m |
2 |
|
|
1 |
|
|
132

Рис. 2.25 |
Рис. 2.26 |
1.10. В установке (рис. 2.26) угол α наклона плоскости к горизонту равен 30°, массы тел одинаковы ( m = 1 кг). Считая нить и блок невесомыми и пренебрегая трением в оси блока, определить силу давления на ось, если коэффициент трения между наклонной плоскостью и лежащим на ней телом
μ= 0,1. [ F = mg(1 +μcosα + sin α)cos( π4 − α2 ) = 13,5 Н.]
2 Центр масс системы материальных точек и закон его движения
Уровень 1
2.1. Определить положение центра масс системы, состоящей из четырех шаров, массы которых равны соответственно m, 2m ,3m, 4m . Шары распо-
ложены по вершинам квадрата (рис. 2.27). Расстояние между соседними шарами равно 15 см. [Xc = 7,5 см, Yс = 4,5 см.]
Рис. 2.27 |
Рис. 2.28 |
2.2.Определить положение центра масс системы, состоящей из четырех шаров, массы которых равны соответственно m, 2m, 3m, 4m . Шары распо-
ложены по четырем смежным вершинам куба (рис. 2.27). Расстояние между соседними шарами 15 см. [Xc = 1,5 см, Yс = 4,5 см, Zс = 3 см.]
2.3. Определить центр масс однородной проволоки длиной L, согнутой посередине под прямым углом. [от вершины по биссектрисе на расстоянии
L8 2 .]
133
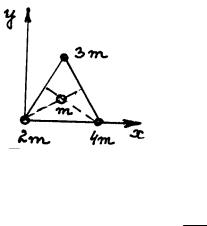
2.4. Лодка массой m1 = 120 кг была неподвижна на поверхности воды. Человек массой m2 = 80 кг переходит из одного конца лодки в другой. В ре-
зультате лодка переместилась на расстояние S = 80 см. Не учитывая сопротивление воды, определить длину лодки
[l = S m1 + m2 = 2 м.] m2
2.5.Плот массой m1 = 400 кг, длиной l = 10м неподвижен на стоячей воде. Два мальчика с массами m = 60 кг и m3 = 40 кг стоят на разных концах пло-
та. Мальчики начинают одновременно двигаться навстречу друг другу с одинаковыми скоростями и, встретившись, останавливаются. На какое расстоя-
ние в результате сдвинется плот? [ S = |
m2 − m3 |
|
l = 0,2 м.] |
|||
2(m |
+ m |
2 |
+ m |
) |
||
|
1 |
|
3 |
|
|
|
2.6. Два шара с одинаковыми радиусами R =10 см, цинковый и алюминиевый скреплены в точке касания. Определить центр масс, полученной системы. Плотность цинка ρ1 = 7,1 × 103 кг/м3, алюминия — ρ2 = 2,7 × 103 кг/м3.
[Х = 0,53 R = 5,3 см от центра масс цинкового шара.]
2.7.Масса Луны составляет 1,2 % массы Земли. Расстояние между Землей
иЛуной составляет 384 000 км. Определить положение центра масс системы Земля–Луна [4553 км от центра Земли.]
Уровень 2
2.8. К аэростату М прикреплена веревочная лестница длиной l , на нижнем конце которой находится человек. Определить массу человека, если известно, что, поднявшись по лестнице до ее верхнего конца, человек переместился
по отношению к Земле вверх на высоту 0,9 |
l . [ m = |
M |
.] |
|
|
9 |
|
2.9. Определить координаты центра масс системы, состоящей из четырех шаров массами 2m, 3m, 4m, m , которые расположены в вершинах и в цен-
тре равностороннего треугольника со стороной a = 20 см (рис. 2.29) [Xc = 12
см; Yс = 5,77 см.]
Рис.2.29
2.10. Определить положение центра масс половины круглого диска ра-
диусом R, считая его однородным. [На расстоянии 43Rπ от центра.]
134
3 Импульс. Закон сохранения импульса
Уровень 1
3.1. Человек массой m1 = 60 кг бежит со скоростью υ = 8 км/ч и догоняет тележку массой m2 = 80 кг, которая движется со скоростью υ2 = 2,9 км/ч. С
какой скоростью u будет двигаться тележка, если человек прыгнет на нее? С какой скоростью u′ будет двигаться тележка, если человек бежит навстречу ей? [u = 5,14 км/ч; u′ = 1,71 км/ч.]
3.2.Граната, летящая со скоростью υ = 10 м/с, разорвалась на два осколка. Больший осколок, масса которого составляла 0,6 массы всей гранаты,
продолжал двигаться в прежнем направлении, но с увеличенной скоростью υ1 =25 м/с. Определить скорость υ2 меньшей части гранаты. [ υ2 =-12,5 м/c.]
3.3.На подножку вагонетки, которая двигалась прямолинейно со скоростью 2 м/с, прыгнул человек массой m2 = 60 кг в направлении, перпендику-
лярном ходу вагонетки. Масса вагонетки m1 = 240 кг. Определить скорость
вагонетки вместе с человеком. [ υ = |
m1υ1 |
|
= 1,6 м/с.] |
|
m +m |
2 |
|||
|
|
|||
|
1 |
|
3.4.Платформа с песком общей массой М = 2 т стоит на рельсах на горизонтальном участке пути. В песок попадает снаряд массой m = 8 кг и застре-
вает в нем. Не учитывая трения, определить, с какой скоростью будет двигаться платформа, если в момент застревания скорость снаряда υ = 450 м/с, а
еенаправление — сверху вниз под углом α = 30° к горизонту [1,55 м/с.]
3.5.Лодка массой 80 кг отплывает от берега со скоростью υ, направленной под углом 30° к линии берега. С берега на лодку с разгона прыгает юно-
ша массой 40 кг со скоростью 6 м/с, перпендикулярной линии берега. При этом лодка продолжает движение под углом 60° к линии берега. Определить первоначальную скорость лодки. [3 м/с.]
3.6.Материальная точка массой 1 кг, двигаясь равномерно, описывает четверть окружности радиусом R = 1,2 м за 2 с. Определить модуль изменения импульса точки за это время. [1,3 кг · м/с].
Уровень 2.
3.7.Конькобежец массой M = 70 кг, стоя на льду, бросает в горизонтальном направлении камень массой 3 кг со скоростью 8 м/с. На какое расстояние S откатится при этом конькобежец, если коэффициент трения коньков о лед
µ= 0,02? [S = 0,3 м.]
3.8.На железнодорожной платформе, которая движется со скоростью υ =
=5 м/с, закреплено орудие. Масса платформы с орудием М = 104 кг. Из орудия вылетает снаряд массой m = 25 кг под углом α = 60° к горизонту. Начальная скорость снаряда относительно орудия u = 500 м/с. Определить ско-
135

рость платформы в случаях, когда: 1) орудие стреляет в сторону движения платформы; 2) против движения платформы.
[ υ = (M + m)υ − m(υ+ u cosα) |
= 4,37 м/с, |
υ |
2 |
= 5,6 м/с.] |
|
1 |
M |
|
|
|
|
|
|
|
|
|
|
3.9. Частица 1 сталкивается с частицей 2, в результате чего получается составная частица. Определить ее скорость υ и модуль скорости υ, если из-
вестно, что масса частицы 2 в два раза больше массы частицы 1, а их скоро- |
|||||||
|
|
|
|
|
r |
r |
= 4i −5 j . |
сти перед столкновением — υ1 |
= 2i +3 j,υ2 |
||||||
r |
(υ + 2υ |
2 |
) |
|
,υ 4 м/с.] |
|
|
[ υ = |
1 |
|
3 |
|
|
||
|
|
|
|
|
|
|
|
3.10. На катере массой m = 4,5 т находится водомет, выбрасывающий со скоростью u = 6 м/с относительно катера назад µ = 25 кг/с воды. Пренебрегая сопротивлением движению катера, определить: 1) скорость катера через t = 3 мин после начала движения; 2) предельно возможную скорость катера.
[1) 3,8м/с; 2) 6м/с.]
Уровень 3
3.11. Имеется кольцо радиусом R. Радиус проволоки равен r , плотность материала проволоки равна ρ. Найти силу F, с которой это кольцо притяги-
вает материальную точку массой m , находящуюся на оси кольца на расстоянии L от ее центра.
3.12. На тележке массой М = 20 кг, которая может свободно перемещаться вдоль рельс, лежит доска массой m = 4 кг. Коэффициент трения между доской и тележкой k = 0,2. Доску тянут с силой F, направленной горизонтально (рис. 2.30). Найти ускорение доски и силу трения между доской и тележкой в двух случаях: 1) F = 5,9 Н; 2) F = 19,6 Н.
Рис 2.30
3.13. Акробат массой М = 50 кг, имея при себе груз m = 5 кг, прыгает под углом α = 60° к горизонту со скоростью υ0 = 6 м/с. В наивысшей точке своей
траектории он бросает груз горизонтально назад с относительной скоростью υ = 2 м/с. На сколько увеличится дальность прыжка акробата вследствие
этого?
136

4 Работа. Мощность. Кинетическая энергия
Уровень 1
4.1. Тело массой 5кг поднимают с ускорением 2 м/с2. Определить работу силы в течение первых пяти секунд [1,48 кДж.]
4.2.Насос мощностью P используют для откачки нефти с глубины h . Определить массу жидкости, поднятой за время t , если к. п. д. насоса равен
η. [ m = ηghPt .]
4.3.Материальная точка массой m = 1 кг двигалось под действием не-
которой силы согласно уравнению: S = A − Bt +Ct2 − Dt3 (B = 3 м/с, C = 5м/с2 D = 1 м/с3). Определить мощность P, затраченную на движение точки в момент времени t = 1 c [16 Вт.] r r
4.4. Находясь под действием постоянной силы F = (3i +10 j +8k ) (H),
частица перемещается из точки с координатами (1, 2, 3) м в точку с координатами (3, 2, 1) м. Определить: а) какая при этом выполняется работа; б) изменениекинетическойэнергиичастицы[а) A = −10 Дж; б) Wk = −10 Дж].
4.5. Тело массы m брошено под углом α к горизонту с начальной скоростью υ0 . Не учитывая сопротивления воздуха, определить среднее значе-
ние мощности действующей силы за время подъёма тела. [ P
P = − 12 mgυ0 sin α.]
= − 12 mgυ0 sin α.]
Уровень 2
4.6. Какую мощность должен развивать трактор при перемещении прицепа массой m =5 ×·103 кг в гору со скоростью υ = 1 м/с, если угол наклона α=20°, а коэффициент трения μ = 0,2.
[ P = mgυ(sin α +μcosα) =26кВт].
4.7. На автомобиль массой М =1т во время движения действует сила трения Fòð , равная 0,1 действующей на него силы тяжести mg. Какую массу
m бензина расходует двигатель автомобиля на то, чтобы на пути S = 0,5 км увеличить скорость движения автомобиля от υ1 = 10 км/ч до υ = 40 км/ч?
К.п.д. двигателя η = 0,2, удельная теплота сгорания бензина q = 46 мДж/кг. [m = 0.06 кг].
4.8.Тепловоз массой m = 106 кг поднимается в гору с углом наклона
α=10º со скоростью 15 м/с и проходит путь 2 км. Определить работу и среднюю мощность тепловоза на этом пути, если коэффициент трения μ равен
0,05. [ A = Smg(sin α +μcosα) = 4,4 × 10 9 Дж;  P
P = mg(sin α+μcosα)υ= 3,3 107 Вт.]
= mg(sin α+μcosα)υ= 3,3 107 Вт.]
137

4.9 Наклонная плоскость составляет с горизонтом угол α =30º. Тело движется вверх по наклонной плоскости из определённой точки с начальной скоростью 10м/с. Коэффициент трения равен 0,1. Определить скорость тела при его возвращении в первоначальную точку, а также высоту подъёма тела.
|
[ υ = υ0 |
sin α −μcosα |
= 8,35 м/с; |
h = |
υ0 |
2 sin α0 |
|
= 4,35 м.] |
|
|
sin α +μcos |
α |
2g(μ×cosα +sin α |
||||||
|
|
|
|
|
|||||
Fr |
4.10. Тело массой |
m |
начинает |
двигаться под |
действием силы |
||||
= 2tir + 3t2 rj . Определить мощность P(t) , развиваемую силой в момент |
|||||||||
времени t .
[ P(t) = (2t3 + 3t5) m .]
Уровень 3
4.11. Мяч радиусом R = 10 см плавает в воде так, что его центр масс находится на Н = 9 см выше поверхности воды. Какую работу А надо совершить, чтобы погрузить мяч в воду до диаметральной плоскости?
[А = 0,74 Дж.]
5. Потенциальная энергия. Закон сохранения механической энергии
Уровень 1
5.1.Тело массой 0,5 кг брошено вертикально вверх со скоростью 20 м/с. За всё время полёта сила сопротивления воздуха совершила работу, модуль которой равен 36 Дж. Найти скорость тела во время падения на зем-
лю [16м/с.]
5.2.Гиря массой m = 10кг падает с высоты h =0,5м на подставку, скреплённую с пружиной жёсткостью k = 30 Н/см. Определить при этом смещение пружины Х. [21,6см.]
5.3.Определить работу силы тяжести при перемещении массы m из точки В (рис. 2.31 ) в точку С [ A = 2mg .]
Рис. 2.31 |
Рис. 2.32 |
138

5.4. В точке О находится материальная точка массой М, которая образует гравитационное поле. Определить работу гравитационной силы при перемещении материальной точки массой m из точки В (2, 0, 0) в точку С (0, 2, 0)по дуге окружности соединяющей эти точки (рис. 2.32). [А = 0.]
|
x |
|
y |
||
5.5. Потенциальная энергия частицы имеет вид: Wï |
= a |
|
− |
|
, где |
y |
|
||||
|
|
|
z |
||
a = const . Определить силу F, действующую на частицу, а также работу А, совершенную силой при переходе частицей из точки (1, 1, 1) в точку (2, 2, 3).
[ Fr = a ×[- 1y ir + ( yx2 + 1z ) × rj − kr]; A = − a3 .]
5.6. Зависимость потенциальной энергии Wï тела в центральном сило-
вом поле от расстояния r до центра поля задаётся функцией Wï = rA2 − Br ,
(A =6 мкДж · м2, В = 0,3 мДж · м).
Определить, при каких значениях r максимальное значение принимают:
2.потенциальная энергия тела;
3.сила, действующая на тело.
[1)r = 2BA = 4 см; 2) r = 3BA = 6 см.]
5.7. С башни высотой Н = 20 м брошен горизонтально со скоростью υ0 = 10 м/с камень массой m = 400 г. Не учитывая сопротивления воздуха,
определить для момента времени t = 1 c после начала движения кинетическую и потенциальную энергию камня.
[39,2 Дж; 59,2 Дж.]
Уровень 2
5.8. Тело массой m = 0,5 кг бросают со скоростью υ0 = 10 м/с под уг-
лом α = 30º к горизонту. Не учитывая сопротивления воздуха, определить кинетическую энергию Wk , потенциальную энергию Wï и полную механиче-
скую энергию тела W через t = 0,4 с после начала движения, а также, в верхней точке траектории.
[Wk =19Дж; Wï =5,9 Дж; W = 24,9 Дж; Wk =18,7Дж; Wï = 6,2 Дж;
W= 24,9 Дж.]
5.9.Тело массой m соскальзывает с наклонной плоскости высотой h =
=10 см и длиной l = 1 м. Коэффициент трения тела на всём пути μ = 0,04.
Определить кинетическую энергию тела в конце наклонной плоскости, а также путь, который проходит тело по горизонтальному участку до остановки.
139

[0,24 Дж; 1,53 Дж.]
5.10. Сила, действующаяr на тело в некотором поле консервативных сил, описывается законом: F = A( yi + xj) , где A — некоторая постоянная. Определить потенциальную энергию Wï (x, y) тела в этом поле.
[Wï (x, y) = −Axy + C, где C − постоянная].
6 Применение законов сохранения импульса
имеханической энергии к абсолютно упругому
иабсолютно неупругому ударам
Уровень 1
6.1. Тело массой m1 = 1 кг, движущееся горизонтально со скоростью υ1 =1 м/с, догоняет второе тело массой m2 = 0,5 кг и неупруго соударяется с
ним. Какую скорость получат тела, если: а) второе тело стояло неподвижно;
б) второе тело двигалось со скоростью υ2 = 0,5 м/с в направлении,
противоположном направлению движения первого тела; в) второе тело двигалось со скоростью υ2 = 0,5 м/с в том же направле-
нии, что и первое тело.
[à) 0,67 ì / ñ; á) 0,83 ì / ñ; â) 0,5 ì / ñ]
6.2. Тело массой m1 = 3 кг движется со скоростью υ1 = 4 м/с и ударяет-
ся о неподвижное тело с такой же массой. Считая удар центральным и неупругим, найти количество теплоты Q, выделившейся при ударе.
[12 Дж.] 6.3. Два тела движутся навстречу друг другу с соударяются неупруго.
Скорости тел до удара были υ1 = 2 м/с; υ2 = 4 м/с. Общая скорость тел после удара υ = 1 м/с и по направлению совпадает с направлением скорости υ1 .
Во сколько раз кинетическая энергия первого тела больше кинетической энергии второго тела?
[ Wk1 = 1,2.]
Wk2
6.4. Стальной шарик массой m = 20 г, падая с высоты h1 = 1 м на стальную плиту, отскакивает от неё на высоту h2 = 81 см. Найти импульс си-
лы F t , полученный плитой за время удара, и количество теплоты Q, выделившейся при ударе.
[0,17 H·c; 7,2 Дж.]
6.5. Нейтрон (масса m0 ) ударяется о неподвижное ядро урана (m = 235m0 ) . Считая удар центральным и упругим, найти, какую часть скорости υ потерял нейтрон при ударе.
[ |
υ |
= |
2 |
]. |
|
υ |
236 |
||||
|
|
|
140

Уровень 2
6.6. Тело массой m1 = 2 кг движется со скоростью υ1 = 3 м/с и нагоняет тело массой m2 =8 кг, движущееся со скоростью υ2 = 1 м/с. Считая удар центральным, найти скорости υ1 и υ2 тел после удара, если удар:
а) неупругий; б) упругий. |
|
[ a)υ1 = υ2 =1,8 м/c; á)υ1 = 0,6 м/c, |
υ2 = 2,6 м/c]. |
6.7. Каково должно быть соотношение между массами m1 и m2 тел предыдущей задачи, чтобы при упругом ударе первое тело остановилось?
m1 = 1 .m2 3
6.8. Два шара с массами m1 = 0,2 кг и m2 = 0,1 кг повешены на нитях
одинаковой длины так, что они соприкасаются. Первый шар отклоняют на высоту h0 = 4,5 см и опускают. На какую высоту h поднимутся шары после
удара, если удар: а) упругий; б) неупругий.
[à) h1 = 0,005 ì , h2 = 0,08 ì ; á) h = 0,02 ì. ]
6.9.Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нём. Масса пули в 1000 раз
меньше массы шара. Расстояние от центра шара до точки подвеса стержня l = 1м. Найти скорость υ пули, если известно, что стержень с шаром отклонился от удара пули на угол α = 10о.
[ υ = 550 м/c.]
6.10.Стальной шарик, падая с высоты h1 = 1,5 м на стальную плиту,
отскакивает от неё со скоростью υ2 = 0,75υ1 , где υ1 — скорость, с которой он подлетает к плите. На какую высоту h2 от поднимется? Какое время t
пройдет с момента падения шарика до второго удара о плиту? [ h2 = 0,84 м, t =1,4 c .]
6.11. Частица массой m , движущаяся со скоростью υ, налетает на покоящуюся частицу массы m 2 и после упругого соударения отскакивает от
нее под углом α =30о к направлению своего первоначального движения. С какой скоростью начнет двигаться вторая частица?
[ υ2 = 2υ3 =1.17υ; β = ark sin(1/ 2) =30°.]
141
5 ОБРАЗЕЦ КОНТРОЛЬНЫХ ЗАДАНИЙ ДЛЯ ПРОВЕРКИ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ
Iуровень (репродуктивный)
1.Какие системы отсчета называются инерциальными?
2.Закон изменения импульса системы материальных точек.
3.Закон движения центра масс системы материальных точек.
4.Формула для вычисления работы переменной силы.
5.Формулировка и запись теоремы о кинетической энергии системы материальных точек.
6.Чему равна работа консервативной силы по замкнутой траектории?
7.Связь потенциальной энергии и консервативной силы.
8.Формулировка закона сохранения механической энергии.
9.Задача.
Под действием силы 10 Н тело движется прямолинейно так, что зависимость пройденного телом пути от времени дается уравнением
S = A − Bt +Ct2 , где C = 1 м/c2. Найти массу тела.
II уровень (продуктивный)
2 Найти выражение работы силы гравитационного притяжения массы m к массе M при перемещении массы m из точки, находящейся на расстоя-
нии r1 от M , в точку, находящуюся на расстоянии r2 от нее. Обе массы счи-
тать точечными.
3 Доказать закон изменения механической энергии системы материальных точек.
III уровень (творческий)
Доказать, что произвольное центральное поле сил консервативно. То же самое — для произвольного однородного поля сил.
142
