2.2.4. Похибки при одноразовому непрямому вимірі

Одноразові вимірювання виконуються у тому випадку, коли відомо, що випадкові похибки менші від приладових.

Обчислюється густина пульпи (суміш твердих частинок, завислих у рідині, наприклад мул), що міститься в циліндричній посудині, . Результати одноразових вимірів: маса пульпи, внутрішній діаметр циліндра, рівень пульпи в посудині. Приладові похибки вимірів:,,. Усі приладові похибки даються з надійною ймовірністю. Беручи заокруглене значення числа, ми повинні врахувати похибку заокруглення. В інженерному калькуляторі закладене дуже точне значення числа, і там враховувати похибкуне треба.

1. Обчислюємо шукану величину:

.

2. Згідно з (31) границя довірчого інтервалу при надійній імовірності

.

3. Границя довірчого інтервалу для густини при надійній імовірності

.

4. Остаточний результат записуємо у вигляді:

із надійною ймовірністю .

5. Відносна похибка вимірів

.

2.2.5. Похибки непрямих вимірів за відтворюваних умов

Розглянемо експеримент із визначення в’язкості рідини за швидкістю падіння в ній твердої кульки. Кожного разу кидаємо одну й ту саму кульку, ділянка, час проходження якої вимірюється, теж одна й та сама. Отож, виміри виконуються за відтворюваних умов. Коли швидкість кульки усталюється, рівнодійна сил тяжіння, Архімеда та Стокса дорівнює нулю:

.

(45)

Звідси

.

(46)

Взята з довідника густина матеріалу кульки (сталь) , густина рідини (гліцерин). Довжина відрізку, на якому вимірюється час падіння кульки в рідині, . Прискорення вільного падіння. Діаметр кульки. Систематична (приладова) похибка секундоміра. Результати вимірювань часу падіння кульки та обчислень, необхідних для розрахунку похибки, наведені в табл.2.5.

Таблиця 2.5

Знаходження і

1	120,2	0,97	0,94
2	121,3	0,13	0,02
3	121,8	0,63	0,40
4	122,0	0,83	0,69
5	120,8	0,37	0,14
6	120,9	0,27	0,07
	727,0		2,26

1. Середнє значення часу падіння

.

2. Обчислюємо середнє значення шуканої величини:

.

3. Обчислюємо середню квадратичну (стандартну) похибку середнього:

.

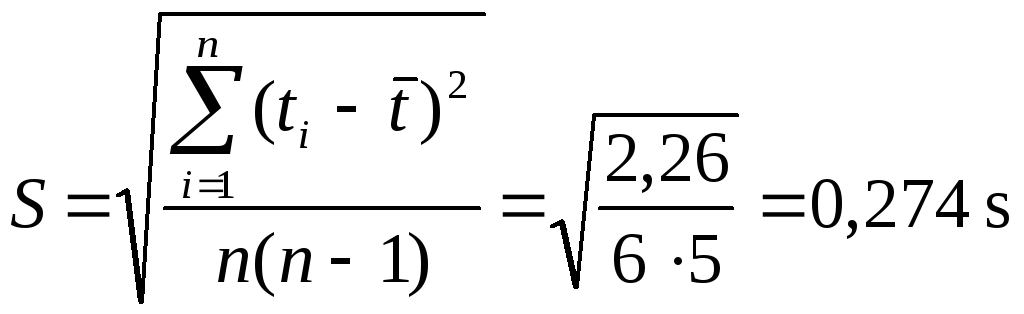4. Оцінюємо випадкову похибку шуканої величини:

.

5. Границя довірчого інтервалу для проміжку часу

.

6. Границя довірчого інтервалу для в’язкості при надійній імовірності

.

7. Границя довірчого інтервалу для в’язкості при надійній імовірності

.

8. Остаточний результат записуємо у вигляді:

з надійною ймовірністю .

9. Оцінюємо відносну помилку вимірів

.

2.2.6. Похибки непрямих вимірів за невідтворюваних умов

Розглянемо експеримент із визначення в’язкості рідини за швидкістю падіння в ній твердої кульки. Кожного разу кидаємо нову кульку, хоча всі інші умови залишаються незмінними. Отож, виміри виконуються за невідтворюваних умов. Чисельні значення такі самі, як і при вимірах за відтворюваних умов. Результати вимірювань діаметра кульки, часу її падіння та обчислень, необхідних для розрахунку похибки, наведені в табл.2.6.

Таблиця 2.6

Експериментальні дані та результати попередніх розрахунків

	, mm	, s	,	,	,
1	1,0	122,2	1,452	0,001
2	1,5	54,8	1,465	0,014
3	1,2	83,2	1,423	0,028
4	1,1	101,4	1,458	0,007
5	1,4	63,0	1,467	0,016
6	1,3	71,8	1,442	0,009
			8,707	

1. Знаходимо значення в’язкості для кожного окремого виміру за формулою (46) і заносимо їх до табл. 2.6.

2. Обчислюємо середнє значення в’язкості для серії вимірів

.

3. Обчислюємо середню квадратичну (стандартну) похибку середнього

.

4. Оцінюємо випадкову похибку шуканої величини

.

5. Оцінюємо систематичну похибку шуканої величини

.

Щоб знайти найбільше можливе значення похибки, підставляємо у формулу мінімальне значення часу .

6. Границя довірчого інтервалу для в’язкості при надійній імовірності

.

7. Границя довірчого інтервалу для в’язкості при надійній імовірності

.

8. Остаточний результат записуємо у вигляді

з надійною ймовірністю .

9. Оцінюємо відносну похибку вимірів

.