Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Университет имени Сулеймана Демиреля

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

11 ALGEBRA

.pdf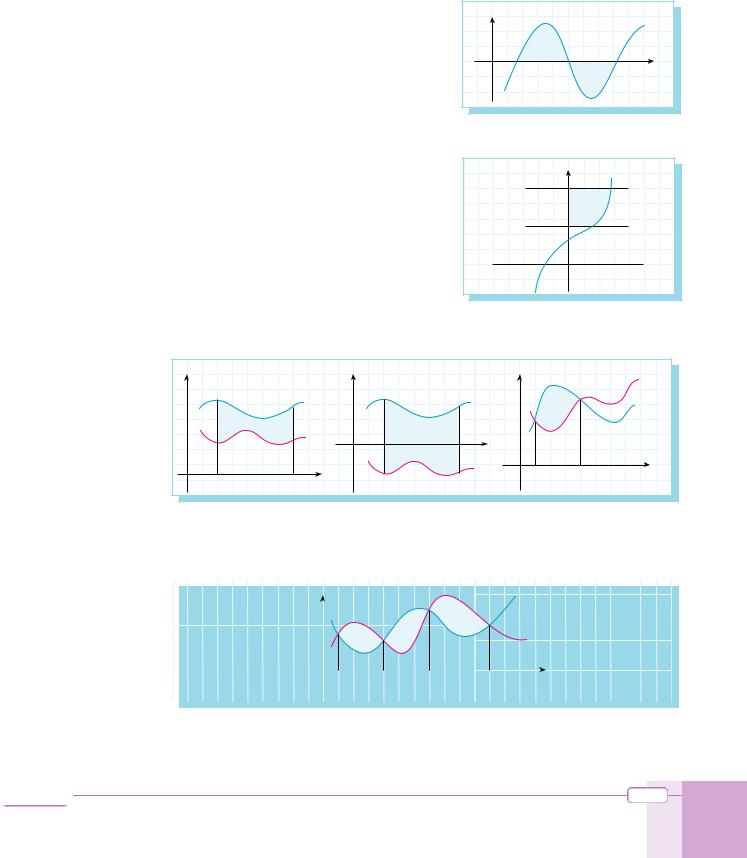

Скачиваний:

Добавлен:

21.02.2016

Размер:

7.9 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 366 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Remember:	y			f(x)
a. The definite integral of f(x) on [a, b] is				f(x)
a. The definite integral of f(x) on [a, b] is
b		A
f (x) dx = A – B.	a		b	x
a	a	B	b
a
b. The area between f(x) and the x-axis on [a, b] is
b. The area between f(x) and the x-axis on [a, b] is
Area = A + B.

3. The area between y = f(x), the y-axis and the

lines y = m and y = n is A = f (y) dy.

yf(x)

4. We can use the formula for the area under a curve to define the area between two curves.
a. y	y	y

						g(x)
	f(x)		f(x)
					A	f(x)
						f(x)
	g(x)		A	x
		a	b	x
		a	b
		x	g(x)	a	b	x
a	b	x	g(x)	a	b
a	b

Let f(x) and g(x) be two curves. Then the area A between f(x) and g(x) on the interval

[a, b] is A = f (x) g(x) dx.

g(x)

f(x)

The area between f(x) and g(x) is

A+ B+ C = ( f(x) g(x)) dx+ (g(x) f(x)) dx+ ( f(x) g(x)) dx.

Integrals

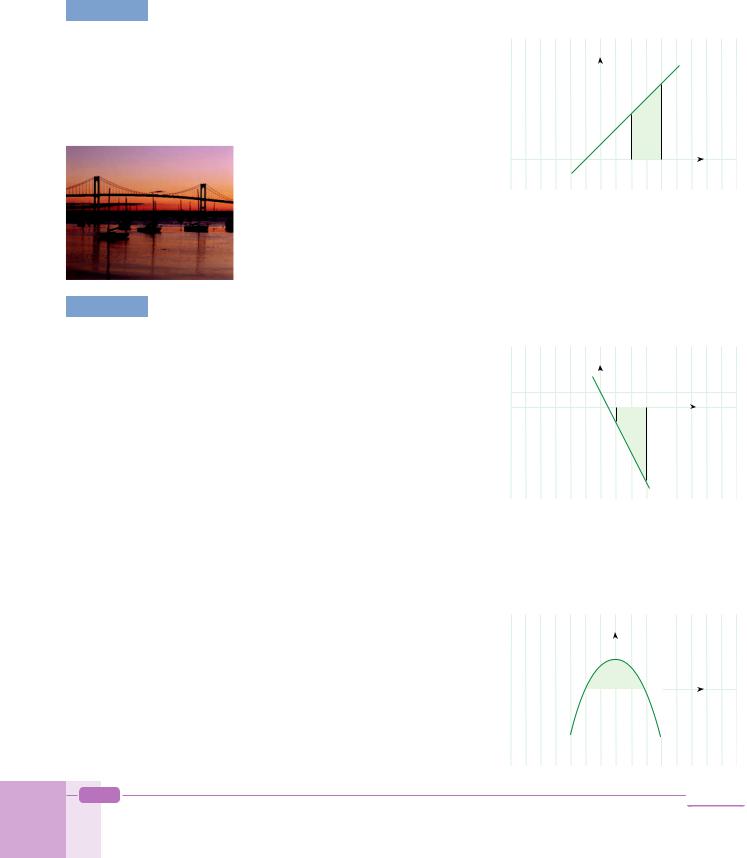
EXAMPLE 77 Find the area A of the region bounded by the graph of y = x + 1, the x-axis, and the lines x = 2 and x = 4.

4	x2	4		y
				y
						y =	x + 1
Solution A = (x+1) dx=		+ x \|
2	2	2
=(8+4) – (2+2)
=(8+4) – (2+2)
= 8.

						A
						A

								x
			–1		2	4		x
			–1		2	4

EXAMPLE 78 Find the area A bounded by the graph of y = –3x + 1, the x-axis, and the lines x = 1 and x = 3.

3		3x2	3		y
3		3x2	3		y
Solution A = ( 3x+1) dx=			x \|
1		2	1

				1		1	3
=(27 3) ( 3 1)				1						x

						1
2	2					1

						3	A
						3	A
= 21	1
= 21	1
2	2
=10.
=10.								y	= –3x + 1

	79 What is the area of the finite region between the graph of y = 1 – x2 and the x-axis?
EXAMPLE

Solution f(x) = 1 – x2 = 0 x = 1
Solution f(x) = 1 – x2 = 0 x = 1								y
1		2			x3	1		y


									1
	A = (1 x		) dx= x			\|
	1				3	1	–1	A		1
	=(1	1) ( 1		1)				A			x



= 4.		3		3

										y = 1 – x2
3
3

60	Algebra 11

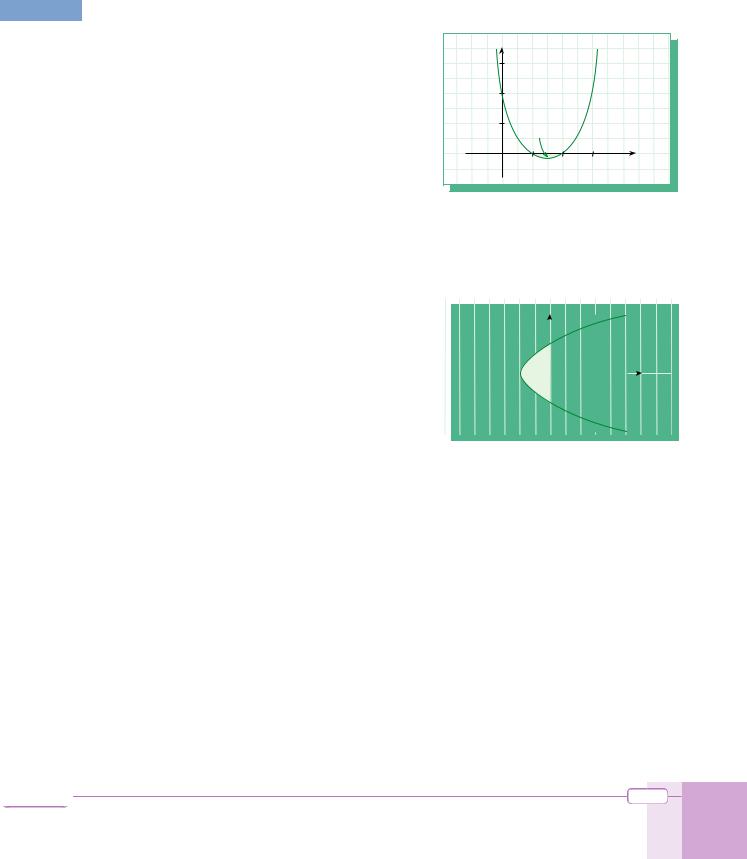
EXAMPLE 80 What is the area of the finite region between the graph of y = 2 – 3x + x2 and the x-axis?

Solution	2 – 3x + x2 = 0 x				= 1, x = 2					y	y = 2 – 3x + x2
Solution	2 – 3x + x2 = 0 x			1	= 1, x = 2					3
				1		2				3
	2	2	) dx=			2x+	3x2	x3	2	2
	A = (2	3x+ x	) dx=			2x+	2	3	\|
	1						2	3	1
		8			3	1				1	A
		8			3	1
	=(–4+6 – 3) – (–2+				2 – 3)
	=(–4+6 – 3) – (–2+				2 – 3)								x
	= 1.									1	2	3	x
										1	2	3

	6

	81 Find the area of the region bounded by the graph of y2 – 1 = x and the y-axis.
EXAMPLE

Solution y2 – 1 = 0 y = ± 1								y	y2	– 1 = x
Solution y2 – 1 = 0 y = ± 1								y	y2	– 1 = x
1				3	– y)\|		1
1				3
	A = (y2 1) dy= – ( y
					1
	1		3		1		A
	1	1	1								x

						–1
						–1
	= (	3	1)+( 3+1)				–1
	= (	3	1)+( 3+1)
= 4.


3
3

Check Yourself 15

1.Find the finite area between the graph of y = x2 – 4 and the x-axis.

2.Find the area of the region bounded by y = 2x2 – 4x + 5, the x-axis, and the lines x = 2 and x = 3.

3.What is the area of the region bounded by y = 3x + 5, the x-axis, and the lines x = 1 and

x= 4?

4.Find the area of the region bounded by the graphs of y = 5x + 1, the y-axis, and the lines

y= 2 and y = 3.

5.Find the area of the region bounded by the graph of y2 = x + 9 and the y-axis.

Answers
1.	32	2.	23	3.	75	4.		3	5. 36
	3		3		2		10

Integrals

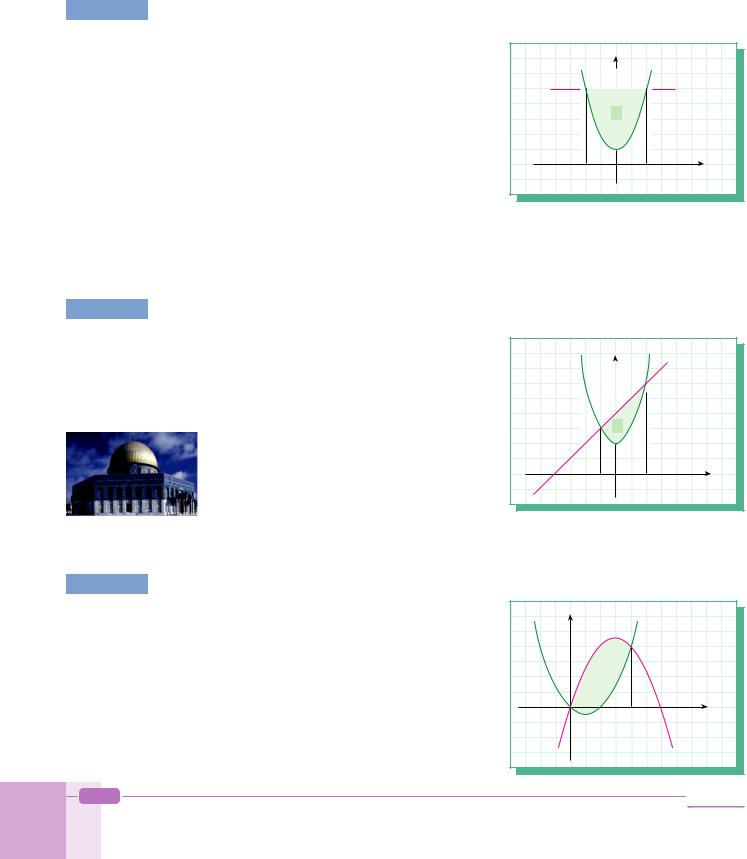
EXAMPLE 82 Find the area of the finite region between the graphs of y1 = x2 + 1 and y2 = 5.

Solution Before we begin, we need to find the interval for the integration. If we sketch a rough graph we can see that the interval is set by the intersection of the two lines. Therefore, we need to solve the two functions simultaneously to find the upper and lower limits for the integral. Then we can find the definite integral between the limits.

y1	= x2 + 1		= y2	x2 + 1 = 5 x = ± 2
y2	= 5	y1

	y
	y	= x2 + 1
	1
	5	y2 = 5
		y2 = 5
	A
	1	x
–2	2	x
–2	2

2			2				x3	2	8	8	32
A =	(5 (x	2	+1)) dx=	2		4x	x3	2	8	8	32
A =	(5 (x		+1)) dx=	(4 x	) dx=	4x		\| =(8	) ( 8+	)=		.
2			2				3	2	3	3	3

EXAMPLE	83	Find the area of the region bounded by y1	= x2 + 2 and y2	= x + 4.

Solution	Again, we find the interval by solving the two														y y1 = x2 + 2
	functions simultaneously.															y2 = x + 4
	y1 = y2			x2 + 2 = x + 4
	x1 = 2 and x2 = –1														4
		2							2						A
	A = ((x+4) (x2 +2)) dx=								( x2 + x+2) dx						2
		1							1						2
		1							1					–4
			x3		x2		2	8		1		1		–4		x
	=		x3	+	x2		2	8	+2+4) (	1	+	1	2)	–1	2	x
	=		3	+	2	+2x	\| =(	3	+2+4) (	3	+	2	2)	–1	2
			3		2		1	3		3		2
	=	9 .
		2

EXAMPLE 84 Find the area of the region bounded by f(x) = x2 – x and g(x) = 3x – x2.

Solution	f(x) = g(x)									y		f(x) = x2 – x
Solution	f(x) = g(x)
	x2 – x = 3x – x2
	So x1 = 0, x2 = 2.
	2							2			A
	2							2
	A = ((3x x2 ) (x2					x)) dx= ( 2x2 +4x) dx					1	2	3	x
	0							0			1	2	3
		2x3	+2x	2	2		16	+8 0 =	8	.
	=	3	+2x		\|=		3	+8 0 =	3	.
		3			0		3		3				g(x) = 3x – x2

62	Algebra 11

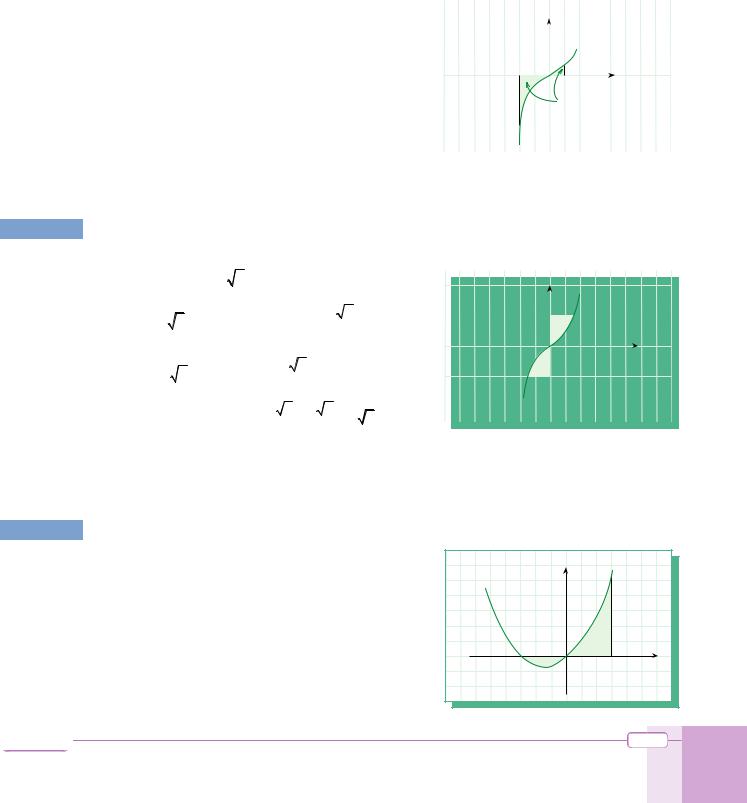
	85 Find the finite area between the graphs of y = x3, y = 0, x = –2 and x = 1.
EXAMPLE

Solution The graph intersects the x-axis at the point x = 0,							y
							y
	so part of the area lies above the x-axis and part of

								y = x	3
	it is below the x-axis. Therefore we divide the area							y = x	3
	it is below the x-axis. Therefore we divide the area
	into two parts.
	into two parts.						–2			x
0		1	4		4			1		x
0		1	4		4			1
	A = x3 dx x3 dx = x			\|+ x		\|		A
				0		1
	2	0	4	2 4		0
			4	2 4		0

	= 0 ( 4)+	1	0 = 17.
	= 0 ( 4)+	1	0 = 17.
		4	4

EXAMPLE 86 Find the area of the region bounded by y = x3, x = 0, y = –2 and y = 2.

Solution

EXAMPLE 87

y = x3 x = 3 y.
																y
																y
							4									y = x3

2	2	1			3y					3	3	2		2
2	2	1					3	\|=			3			2		A
A =	3 y dy = y3 dy =						3	\|=								A
						4			2		2						y = 2
0	0								0
0	0								0									x
0		4


		3y3	0			33		2
		3y3	0			33		2							B
B=	3 y dy =	4	\| =			2											y = –2
B=	3 y dy =		\| =												–2		y = –2
2			2												–2
2				3	3 2				33	2
Total area = A + B =							+				= 3		3 2.

					2				2

These two areas are symmetric. Therefore, if we multiply A by 2 we will find the total area.

What is the area of the region bounded by y = x2 + 3x, the x-axis and the line x = 3?

	0						3						y	y = x2 + 3x
	0						3							y = x2 + 3x
Solution	A+ B= (x2 +3x) dx+ (x2 +3x) dx
	3						0
		x3	3x2		0	x3			+	3x2	3
	=	3	2		\|+		3		+	2	\|
		3	2		3		3			2	0			B
			27											B
	= 0 (9		27			9+		27		0	–3	A		3	x
	= 0 (9		2	)+		9+		2		0	–3	A		3
			2					2
	= 27.
Integrals														63

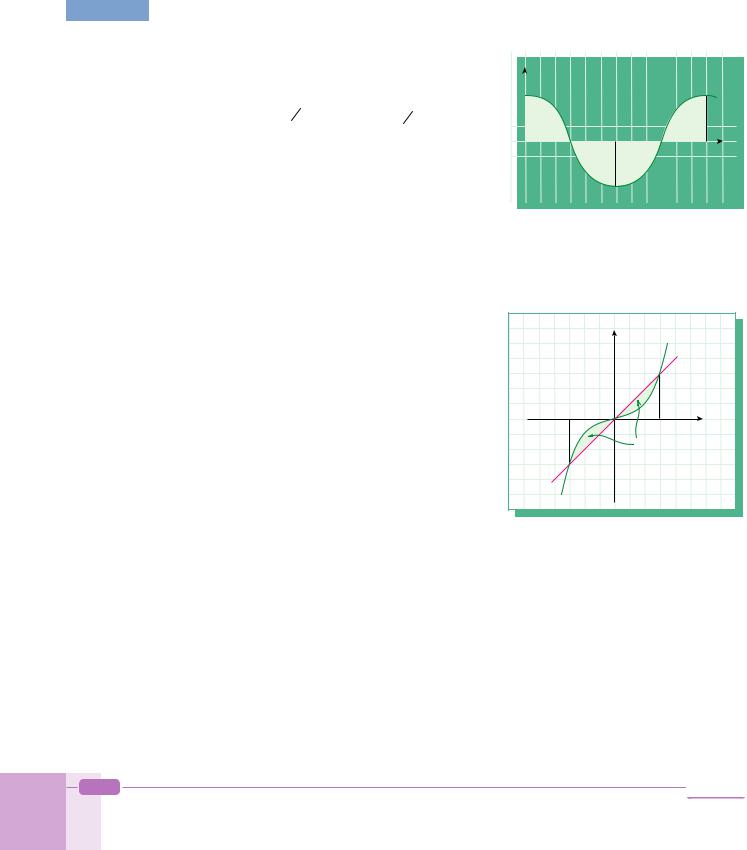
EXAMPLE 88 What is the area of the region between y = cos x and the x-axis on the interval [0, 2 ]?

Solution We can see from the figure that the areas of all

four parts A, B, C, and D are equal. So we can

calculate the answer as follows:

y = cosx

Total area = 4 cos x dx= 4sin x|

= 4sin

4sin0

= 4.

	89	What is the area of the region bounded by the graphs of the functions y		= x3 and y = x?
EXAMPLE			1
				2

Solution First we need to find the intersection points:								y
Solution First we need to find the intersection points:								y2	= x
								y2	= x
y1 = y2									y	= x3
									1
x3 = x; x3 – x = 0; x (x – 1)(x + 1 ) = 0.
So the intersection points are x = –1, 0, 1.								–1
								–1		x
0			1					1		x
0			1					1
A = (x3 x) dx+ (x x3 ) dx								A
1			0
x4	x2	0	x2	x4	1	1	.
=	2	\|+		4	\|=		.
4	2	1	2	4	0	2

Check Yourself 16

1.Find the area of the region bounded by y = x2 + 1 and y = 3x – 1.

2.What is the area of the region bounded by y = 3x2 + 1 and y = 4?

3.Find the area of the region bounded by y = 2x2 + 3x and y = –x2 – 3x + 24.

4.What is the area of the region bounded by the graphs of y = x3 – 2 and y = –2x2 + x?

Answers
1.	1	2. 4	3. 108	4.	37
	6				12

64	Algebra 11

V =

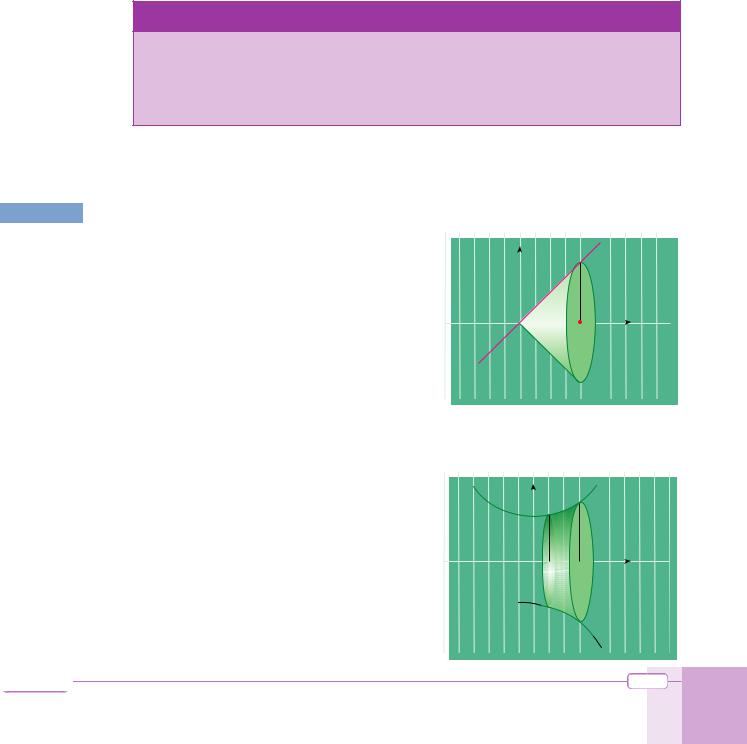
B. OTHER APPLICATIONS

1. Calculating the Volume of a Solid of Revolution

When a region is rotated about an axis we obtain a solid figure. This figure is called a solid of revolution. We can use the definite integral to find the volume of a solid of revolution.

FINDING VOLUME

Let f(x) be a continuous function defined on [a, b]. Then the volume V of the solid generated by rotating the area between the graph of f(x) and the x-axis on [a, b] about the

x-axis is

f (x) 2 dx.

EXAMPLE 90

Solution

Note

f 2x is used in the place of [f(x)]2.

What is the volume V of the solid figure generated by rotating the area between y = 3x and

the x-axis around the x-axis on the interval [0, 2]?
the x-axis around the x-axis on the interval [0, 2]?		y		y = 3x
Look at the figure. Using the theorem we can write				y = 3x




2	2
2	2
V = (3x)2 dx = 9x2 dx
V = (3x)2 dx = 9x2 dx					x
0	0		2		x
	2		2
= 3 x3	2
	\|
	\|
	0
24
24

	91 What is the volume V of the solid obtained by rotating the region between y = x2 + 2 and
EXAMPLE

	the x-axis around the x-axis on the interval [1, 3]?

3							y			y = x2 + 2
							y


Solution V = (x2 +2)2 dx
Solution V = (x2 +2)2 dx
1
3						2
	= (x4 +4x2 +4) dx
	= (x4 +4x2 +4) dx
1											x
5			4x	3				1	3		x
								1	3

	= ( x +			+4x) \|
					3
5			3		1
5			3		1
		1366



15
15

Integrals

Note

If we rotate a figure around the y-axis then the volume is created by x = f(y) and we integrate it with respect to dy:

V = f 2(y) dy.

y = g(x)

EXAMPLE 92 Find the volume V of the solid figure generated by rotating the region between f(x) = 3x – 1, the y-axis, and the lines y = 2 and y = 5 around the y-axis.

Solution To find the volume, we find x in terms of y and														y
integrate the expression with respect to dy:														y = 3x – 1
		x = y+1											5
y 3x – 1		x = y+1
									3
5		+1)2							5	2			2
V = ( y		+1)2				dy= y					2y 1 dy
2		3							2			9		x
	y3		y2				y		5				–1	1
= (	y3	+	y2		+		y		5				–1	3
= (	27	+		9	+		9	) \|
	27			9			9		2
(125 +				25		+ 5			8		4		2 )
	27			9			9		27		9		9
7

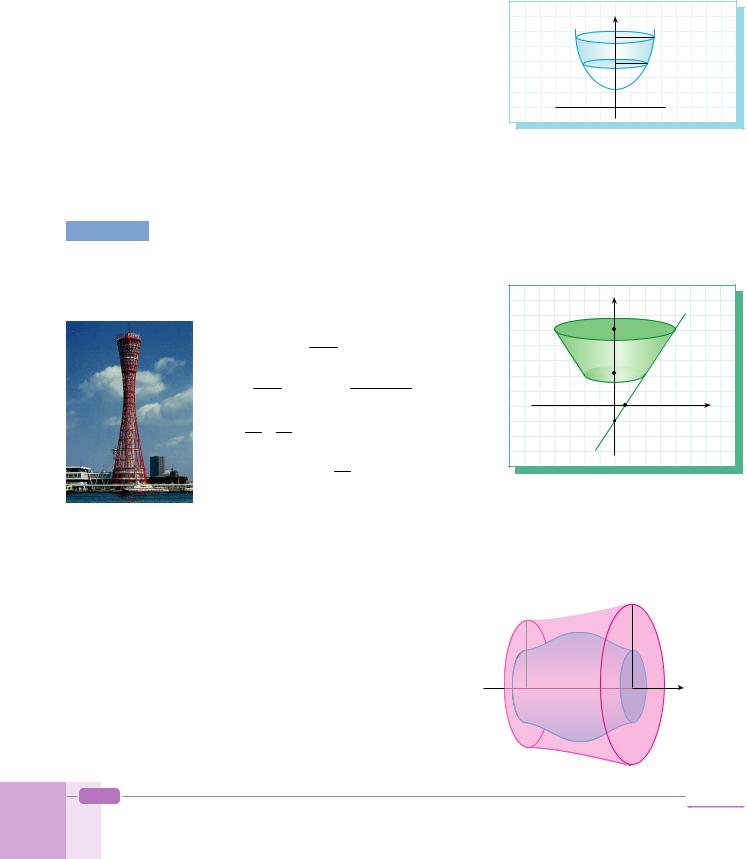
Note

If we rotate the area between two curves f(x) and g(x) on the interval [a, b] then the volume of the solid figure generated is:

y = f(x) y = g(x)

b			x
V = ( f 2(x) g2(x)) dx.	a	b	x
V = ( f 2(x) g2(x)) dx.	a	b
a

66	Algebra 11

	93 Find the volume V of the solid figure which is generated by rotating the area of the region
EXAMPLE

	bounded by the graphs of y = 2x2 + 2 and y = 3 – 2x2 around the x-axis.
					1
Solution 2x2 +2 = 3 – 2x2			x=							y
										y
												y =	2x2 + 2
					2							y =	2x2 + 2
		1/ 2			2						3
											3


	V =	–1/ 2	(3	2x2 )2			(2x2		+2)2 dx	2
		–1/ 2

	= 1/ 2		( 20x2 +5) dx
	= 1/ 2		( 20x2 +5) dx
		–1/ 2
		–1/ 2		3										x
	( 20x

				+5x) \|
							1/ 2
			3				–1/ 2						y = 3 – 2x2
			3										y = 3 – 2x2
			20		5		20	5
			20		5		20	5
		(	24	+	2	) (	24	2	)
			24		2		24	2
	= 10



	3
	94 Find the volume V of the solid figure generated by rotating the area bounded by the graphs
EXAMPLE
	of y = x3 and y = ñx around the x-axis through 60°.

Solution We can solve the equations simultaneously to find the intersection points:

x3			x, x1 0		and x2	1.	y
		60 (total volume)					y = ñx
V =		60 (total volume)
		360
		1	1
	=	1	(( x)2 (x3 )2 ) dx
		6	0				x
		1	1				1
	=	1	(x x6 ) dx
		6	0
	=		2	7	) \|
	=		( x	x	) \|
					1
		6	2	7	0		y = x3

=6 ( 21 71 0)

=584

Integrals

Check Yourself 17

1.Find the volume of the solid figure generated by rotating the area between y = x2 – 4 and the x-axis around the x-axis.

2.Find the volume of the solid figure generated by rotating the area bounded y = 4x – 1, the x-axis, and the lines x = 1 and x = 3 around the x-axis.

3.Find the volume of the solid figure generated by rotating the area bounded by y = 3x2 + 2x + 1, the x-axis, and the lines x = 0 and x = 2 about the x-axis.

4.Find the volume of the solid figure generated by rotating the area bounded by y = 2x + 1, the y-axis, and the lines y = 2 and y = 5 around the y-axis.

5.Find the volume of the solid figure generated by rotating the area bounded by y = 2x2 + x + 2 and the lines y = 1, x = 1 and x = 2 around the x-axis.

6.Use the definite integral to show that the volume of a sphere with radius R is 43 R3 .

Answers

1.	512	2.	326	3.	2134	4.	21	5.	349
	15		3		15		4		5

6.Place a circle at the centre of the coordinate plane and use the equation of circle.

2.Finding the Length of a Curve (Optional)

FINDING LENGTH

The length L of any curve (or line) between the points a and b of a continuous and

differentiable function f(x) is:	b
	L =	1+( f (x))2 dx.
	a

68	Algebra 11

<<< < Предыдущая 1 2 3 4 56 / 366 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.02.201639.42 Кб91 MID TERM Questions.doc
#
21.02.2016659.97 Кб321.Журналистік деп.Журналистік жауапкершілік.doc
#
21.02.2016345.88 Кб21101_final.pdf
#
21.02.20167.9 Mб2111 ALGEBRA.pdf
#
21.02.20167.98 Mб8143023864X_HT5.pdf
#
21.02.2016197.12 Кб111_RK.doc Rus gruppa...History(otvety nepravelniye).doc
#
21.02.2016302.08 Кб192.Журналисті ытары мен міндеттері.doc
#
21.02.20167.28 Mб13321st Century Political Science.pdf
#
21.02.201650.81 Кб5222-1_1.docx