Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Университет имени Сулеймана Демиреля

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

11 ALGEBRA

.pdf

Скачиваний:

Добавлен:

21.02.2016

Размер:

7.9 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 363 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Given a polynomial P(x) to denote its degree we use deg[P(x)].

EXAMPLE 42

3. Integrating Partial Fractions

We use different methods to evaluate integrals of the form QP((xx)) dx, where P(x) and Q(x) are polynomials and Q(x) 0.

The method we choose depends on the partial fraction involved. Let us look at the main possibilities.

1. Q(x)P(x) with deg[P(x)] = deg[Q(x)] – 1

For integrals of this type we use the substitution u = Q(x) and try to find du in terms of P(x) dx. After this, we try to find the answer.

x2 +2x+1 dx =?

Solution		1	dx =	1		dx

	2	+2x+1		(x+1)	2
	x	+2x+1		(x+1)

Let u = x + 1, then du = dx.

1	dx =	1	du = u 2 du =	1	+c =	1	+ c
2		2		u		x+1
(x+1)		u

EXAMPLE 43

Solution

3. Q(x)P(x) with deg[P(x)] < deg[Q(x)] and Q(x) not reducible in R

The expression

dx is given. If = b2 – 4ac < 0 then we can use the following

+bx+c

method to evaluate the integral:

dx =

+bx+c

(mx+n) +r

mx+ n

arctan( mx+ n)+ c

arccot( mx+ n)+ c .

Evaluate

dx.

+4x+5

= arctan( x+2)+ c

+4x+5

+4x+4+1

(x+2)

or = –arccot(x + 2) + c

Integrals

Check Yourself 6

Evaluate the integrals.

x2 +3		1		3					dx
a. x2 +1 dx	b. x2 +2x+5 dx		c. (x+1)4 dx				d. x2 +8x+16
Answers
a. 2arctan x + x + c	b. 1 arctan( x+1)+ c		c.			1 3 + c	d.		1	+ c
	2	2			(x+1)			x+4
4. Integrating Radical Functions
The integration of functions of the form f (x) dx,				n		f (x) dx,	a2 u2		requires the use

of special methods. Let us look at these methods.

1. Integrating Simple Radical Functions

There are many different types of radical function, and we can use different methods to integrate them. In this section we will concentrate on radical functions that can be integrated easily using the methods we have studied. We call these functions simple radical functions.

When integrating a simple radical function, we first try to eliminate the radical sign. For this reason we use substitutions such as u2, u3, etc. depending on the degree of the root.

44 3x+1 dx =?

EXAMPLE

2u du

Solution

To eliminate the root we can substitute u = 3x + 1 (x –

), so 2u du = 3 dx and dx

3 .

= u 2u du

Then 3x+1 dx=

u2 2u du

2 u2

du = 2

+ c=

2(3x+1)2

+ c.

3 5x 2 dx =?

EXAMPLE

Solution To eliminate the third degree root we choose u3 = 5x – 2, then

3u2 du = 5 dx, i.e. dx =

3u2

du.

du = 3u3 du =

So 3 5x 2 dx = 3 u3

3u2

3 u4 + c = 3(5x 2)3

+ c.

30	Algebra 11

	46	x2	+5
EXAMPLE		x		dx = ?
EXAMPLE				dx = ?

Solution Let u2 = x2 + 5 and 2u du = 2x dx, i.e. xdx = udu.

Then	x	dx= u du	= du = u+ c = x2 +5 + c.

	x2 +5	u2

EXAMPLE

dx =?

x 1

Solution Let u2 = x – 1, (x > 1) so 2u du = dx.

Substituting gives

4x 2u

du , so we need to eliminate x.

We can do this by writing x in terms of u, i.e. x = u2 + 1 (from the substitution u2 = x – 1).

Now,

dx = 4 (u2 +1) 2 u du = 8(u2

+1) du

x 1

(x 1)2

= 8 (

+ u)+ c= 8

+( x 1)

+ c.

Check Yourself 7

Evaluate the integrals.

1+4x dx

b. 5

4x 3 dx

2x2 +3

x+1+1 dx

x 1

x+1

Answers

a. (4x+1)3 / 2

5(4x 3)6 / 5

+ c

c. 5

2x2 +3

+ c

d. 2

x3 2

+ c

2(x+ 2) x 1+ c

f. 2 x+1+ x+ c

Integrals

dx =

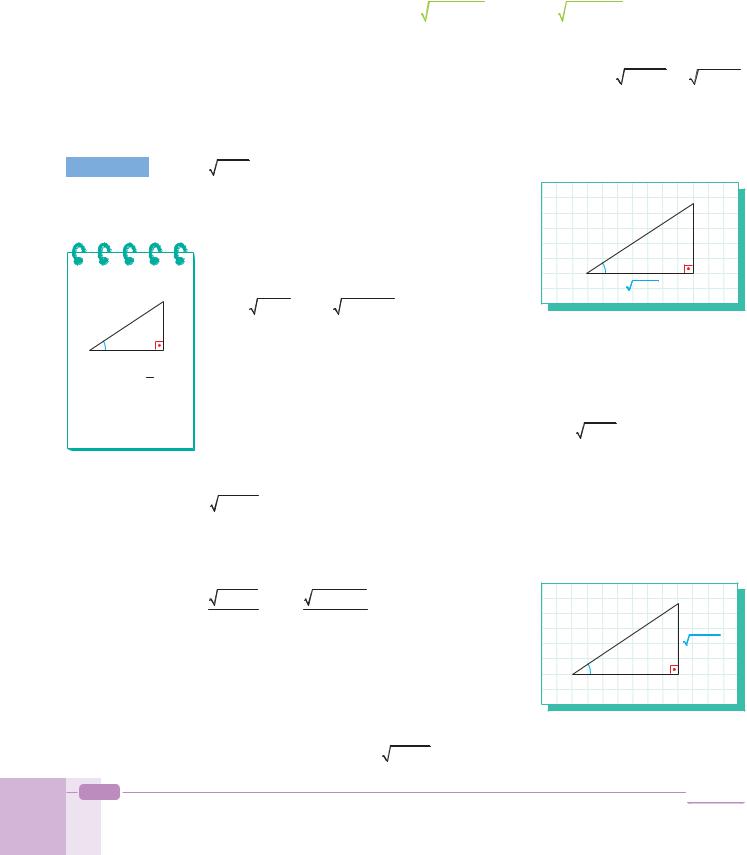
2. Integrals of the Form

a2 ±u2 dx or u2 ± a2 dx

We can evaluate integrals of this kind by using trigonometric substitution.

We begin by drawing a right triangle and labeling the sides a, u, and a2 u2 or	u2 a2 ,
then we integrate the resulting trigonometric expression.

EXAMPLE

48 1 x2

dx =?

Solution

Look at the figure.

Let sin = x, then

cos d = dx,

Trigonometric Ratios

= arcsin x.

in Right Triangle:

Then

1 x2

dx=

1 sin2

cos d

d = 1+cos2 d

cos2

d + 1

cos c

cos2 d =

sin2 + c

sin c

+ 1

2 sin cos + c= arcsin x+

tan b

1 x2 + c.

	49	x
EXAMPLE		4x2 1	dx =?
EXAMPLE			dx =?

Solution Look at the figure. Let 2x = sec then 2 dx = tan sec d and = arcsec 2x, so

4x2 1

sec2 1 tan sec sec 2

=tan tan d = tan2

=(tan2 +1 1) d

=(tan2 +1) d d

		A
	2x
	a
C	1	B

= tan – + c= 4x2 1 arcsec2 x+ c.

32	Algebra 11

EXAMPLE

dx =?

9+4x2

Solution Let

= tan so

3 tan

x =

dx =

. Then

2cos2

9 tan2

9+4x2

2 cos2

9+4

9 cos2

tan2 3 1+tan2

cos

sin2

d .

9cos

sin2

cos2

cos

Now use the substitutions u = sin and du = cos d :

cos

2 =

+ c =

+ c

sin

9sin

2 9

4x2

+ c =

9 4x2

+ c.

9 2x

Check Yourself 8

Evaluate the integrals.

9 x2

9x2

9 x2

Answers

x 9 x2

9x2 +4

2 arcsin(

3)+

+ c

b. arcsin(

3)+ c

+ c

Integrals

5. Integratign Trigonometric Functions

Let us now turn our attention to methods for evaluating the integral of complex trigonometric expressions. In this section, we will use the following basic identities:

sin x dx = cos x+ c

cos x dx = sin x+ c

1. Integrals of the Form sinm x cosn x dx	(m, n N)
Case 1: m and n are both odd numbers

Let m = 2k + 1 and n = 2t + 1, then we can write the integral as sin2k 1 x cos2t x cos x dx. Using the substitutions u = sin x, du = cos x dx and cos2t x = (1 – sin2 x)t we can evaluate the integral.

Alternatively we can write cos2t 1 x sin2k x sin x dx and use the substitutions u = cos x, du = –sin x dx and sin2k x =(1 – cos2 x)k.

	51 Evaluate cos7 x sin3 x dx.
EXAMPLE

Solution		cos7 x sin3 x dx = cos7 x sin2 x sin x dx= cos7 x (1	cos 2	x) sin x dx
		Use the substitutions u = cos x and du = – sin x dx, then
		cos7 x sin3 x dx = u7(1 u2 ) du (u9 u7 ) du = u10	u8 + c = cos10 x		cos8 x	+ c.
		10	8	10	8
		Case 2: one of m or n is odd
		In this situation we reduce the odd power by one by writing, for example,
		sin7 x = sin6 x sin x, or cos3 x = cos2 x cos x.
		Then we can use the substitution u = sin x or u = cos x to evaluate the integral as described
		in Case 1.
	52 Evaluate sin6 x cos3 x dx.
EXAMPLE

Solution		sin6 x cos3 x dx = sin6 x cos2 x cos x dx = sin6 x (1 – sin2 x) cos x dx

Use the substitutions u = sin x and du = cos x dx:

sin6 x cos3 x dx = u6 (1 u2 ) du = (u6	u8 ) du = u7	u9	+ c = sin7 x	sin9 x+ c.
	7	9	7	9

34	Algebra 11

Case 3: m and n are both even numbers

In this situation, we use the following identities to evaluate the integral.

				sin2 x =	1 cos2x
					2
				cos2 x =	1+ cos2x
					2
	53 Evaluate sin2 x cos2 x dx.
EXAMPLE

Solution sin2 x cos2 x dx 1 cos2x		1 cos2x dx = 1 (1 cos2 2x) dx
2			2		4
	= 1 sin2 2x dx =		1	1 cos4x dx = 1		dx	1	cos4x dx
4			4	2	8		8

=8x 81 41 sin4x+ c = 8x sin432 x + c.

2.Integrals of the Form sinmx cosnx dx,

sinmx sinnx dx or cosmx cosnx dx

To evaluate these types of integral we use the following inverse conversion identities:

sin a sin b =		1 cos(a+ b) cos( a b)
		2
sin a cos b =	1	sin(a+ b)+sin( a b)
	2
cos a cos b =	1	cos(a+ b)+cos( a b) .
	2

	54 sin3x cos9x dx=?
EXAMPLE

			2							2
Solution		sin3x cos9x dx	1	sin12x+sin( 6 x) dx= 1							(sin12 x sin6 x) dx
		=	1			1	cos12x+	1	1	cos6 x+ c= cos12x+ cos6 x+ c
		=	2		12		cos12x+	2	6	cos6 x+ c= cos12x+ cos6 x+ c
			2		12			2	6		24	12

Integrals

EXAMPLE 55

cos6x cos2x dx=?

Solution

cos6x

cos2x dx=

1 cos8 x+cos4 x dx= 1

(cos8 x+cos4 x) dx

sin8x+

1 sin4x+ c= sin8x

+ sin4x+ c

Check Yourself 9

Evaluate the integrals.

a. sin3

x cos x dx

b. sin4 x cos5 x dx

c. sin4 x cos4 x dx

d. cos2x cos x dx

e. cos4x sin5x dx

f. sin3x sin5x dx

Answers

a. sin4 x + c

b. sin5 x 2sin7 x

+ sin9 x + c

3x sin4x + sin8x

+ c

128

1024

d. sin3x + sin x + c

e. cos9x cos x

+ c

sin2x

sin8x

+ c

3. Substituting t = tan

This approach is possible for integrands containing only the first power of sin x and/or cos x.

Look at the steps for deriving the identities provided by t = tan( x) :

tan x = t x = 2 arctan t, i.e. dx =

dt.

1+t2

From the figure, sin x

and cos x

1 .

1 t2

1+ t2

Simplifying these expressions gives us

cos

sin x = 2 sin 2

2 = 2

1+t2

1+ t2

= 1+t2 ,

cos x cos2 x – sin2

x =

–

= 1– t2 .

1+ t2

So we have the following result:

36	Algebra 11

THE u=tan(x/2) SUBSTITUTION

sin x =

cos x =

1– t2

dx =

1+t2

1+ t2

EXAMPLE

dx ?

sin x+1

= tan( x) :

Solution

Substitute the identities from t

2 dt

dx =

1+ t2

sin x+1

(t+1)

+2t+1

1+ t2

1+t2

Substituting u = 1 + t and du = dt gives

2dt

2du2

= 2 u 2du =

2 +c =

+ c =

+ c.

(t+1)

1+t

1+tan

Check Yourself 13

Evaluate the integrals.

1 cos x

a. 1+cos x

1– sin x

Answers

a. 2tan

– x+ c

+ c

1– tan

Integrals

Gottfried Leibniz (1646-1716)

Gottfried Leibniz (pronounced 'libe-nits') was born in Leipzig (now in Germany) in 1646. His father was a professor of philosophy in

Leipzig. Unfortunately, Leibniz's father died when Leibniz was six years old, so he was brought up by his mother.

At school, Gottfried learned Latin and Greek, and also studied philosophy, metaphysics and theology. When he was fourteen, he went to Leipzig University and studied philosophy and mathematics for two years before beginning to study law.

In 1672 Leibniz went to Paris and studied mathematics and physics. During this time he made some discoveries concerning the sum of a series.

Leibniz visited London a year later, and became a member of the Royal Society.

When Leibniz returned to Paris he began studying calculus. At that time he was still trying to develop the calculus notation, so his papers and calculations were sometimes difficult to read. However, in 1675, Leibniz wrote a paper that used the f (x) dx notation for the first time. In the same paper he described the product rule for differentiation, and the power rule.

At around this time, Isaac Newton sent a letter to Leibniz which explained some of Newton's results, although he did not describe his methods. Leibniz replied by describing his own results. Unfortunately, Leibniz's letter did not reach Newton for a long time, and Newton decided that Leibniz had stolen his methods. This resulted in many arguments between the two scientists. However, today we can say that Leibnitz and Newton discovered the same rules of calculus independently.

Leibniz's other important achievements in mathematics include the development of a binary system of arithmetic, and his work on determinants. In 1684 he wrote a paper on calculus whose working showed the efficiency of his integral notation. Leibniz also published papers on dynamics and philosophy.

Leibniz died on 14 November 1716 in Hannover, Germany. His findings continued to influence the work of many of the mathematicians, philosophers and physicists who followed him. Today we can see that his calculus notation and methods are just as important as Newton's methods, and for this reason, Leibniz is remembered as one of the two founding fathers of differential and integral calculus.

<<< < Предыдущая 1 23 / 363 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.02.201639.42 Кб91 MID TERM Questions.doc
#
21.02.2016659.97 Кб321.Журналистік деп.Журналистік жауапкершілік.doc
#
21.02.2016345.88 Кб21101_final.pdf
#
21.02.20167.9 Mб2111 ALGEBRA.pdf
#
21.02.20167.98 Mб8143023864X_HT5.pdf
#
21.02.2016197.12 Кб111_RK.doc Rus gruppa...History(otvety nepravelniye).doc
#
21.02.2016302.08 Кб192.Журналисті ытары мен міндеттері.doc
#
21.02.20167.28 Mб13321st Century Political Science.pdf
#
21.02.201650.81 Кб5222-1_1.docx