
11 ALGEBRA
.pdf
Since 3a – 2b = 5 and 3b – 2a = 5, we can write
3a – 2b = 3b – 2a 3a – 3b + 2a – 2b = 0.
The only possible solution to this equation is a = b, since both a > b and a < b will give a result different from zero. Therefore, we have
3a – 2a = 5.
Obviously, a = 2 is a solution. We can also write this equation as
1= 5 ( |
1 a |
2 |
a |
a |
3) +( |
3) |
|
(divide all terms by 3 ), |
which leads us to conclude that 3a – 2a = 5 has a unique solution (can you see why?). Thus a = b = 2 and
log2(x – 3) = a = 2 x – 3 = 22 = 4 x = 7 .
Check Yourself 33
Solve the equations.
a. x + 2x + log2 x = 7 |
b. 9log5(x – 2) – 5log9(x+2) = 4 |
Answers |
|
a. {2} b. {7} |
|
f. Logarithmic Equations with Parameters
Sometimes we may be asked to solve an equation for the values of a parameter which satisfy a specific condition, or to investigate the solution(s) of an equation for different values of a parameter.
|
98 |
Solve 2 logx a + logax a + 3 loga2x a = 0 for x in terms of a. |
|
|
|
|
|
|||||||
EXAMPLE |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||
Solution |
By the existence conditions, a 0, |
x 0, x 1, |
ax 1 and |
a2x 1. |
|
|
|
|||||||
|
|
So we just need to consider positive values of a. Since a = 1 is a special case which gives us |
||||||||||||
|
|
(2 logx 1) + (logx 1) + (3 logx 1) = 0, we conclude that any positive value of x different |
||||||||||||
|
|
from 1 will satisfy the equation in this case. |
|
|
|
|
|
|
|
|||||
|
|
For a 0 and a 1, if we change the bases to a we get |
|
|
|
|
|
|||||||
|
|
2 |
1 |
|
3 |
2 |
1 |
3 |
|
|||||
|
|
|
|
+ |
|
+ |
|
= 0 |
|
+ |
|
+ |
|
= 0. |
|
|
|
loga x |
loga a+ log a x |
loga a2 + log a x |
log a x |
1+ log a x |
2+ log a x |
||||||
Exponential and Logarithmic Functions |
209 |
Substituting loga x = y gives us
2 + |
|
1 |
+ |
3 |
= 0 2(y+1)(y+2)+ y (y+2)+3y (y+1) = 0 |
|||||||
1+ y |
2+ y |
|||||||||||
y |
|
|
|
y(y+1)(y+2) |
|
|
|
|||||
6y2 +11y+4 = 0 (3y+4)(2y+1)= 0 y = – 4 and y = – 1. |
||||||||||||
|
|
|
|
|
|
|
|
1 |
3 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
The corresponding values of x are |
|
|
|
|
|
|||||||
loga x = y = – 4 x = a– |
4 |
|
1 x = a– |
1 |
|
|||||||
3 and |
loga x = – |
2 . |
|
|||||||||
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
for a 0 |
|
|
||
Hence the solution set is |
{a–1/2, a–4/3} |
for a > 0 and a 1 |
|
|||||||||
|
|
|
|
|
x (0, 1) |
(1, ) |
for a = 1. |
|
|
|||
EXAMPLE 99
Solution
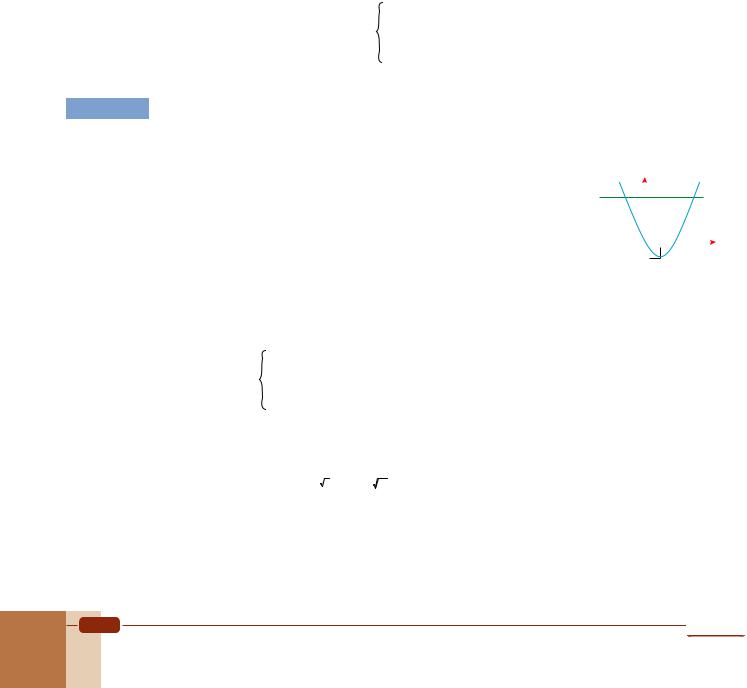
Determine the number of solutions to (log32 x) – (2 log 3 x)= m for different values of m.
Substituting u = log3 x gives us u2 – 2u = m. |
|
|
|
|
|
|
|
|
|
|
|
Let us consider each side of this equation as a function and |
y |
|
|
|
y = u2 – 2u |
||||||
sketch the graph of each function, as shown opposite. |
|
|
|
|
|
|
|
|
|
y = m |
|
|
|
|
|
|
|
|
|
|
|
||
As we can see, one graph is a parabola and the other is a |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
horizontal line. In addition, the graphs intersect at two points |
|
|
|
1 |
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
when m > – 1 and at one point when m = –1, and they do not |
-1 |
|
|
1 |
|
2 3 |
|
||||
|
|
|
|
|
|
|
|
|
|
||
intersect when m < –1. In other words, the equation u2 – 2u = m |
|
|
|
|
|
|
|
|
|
|
|
has two solutions for m > –1, one solution for m = –1 and no |
|
|
|
|
|
|
|
|
|
|
|
solutions for m < –1. Since u = log3x is a one-to-one function, it has the same number of solutions for the different values of m. Hence we conclude that the given equation has
two solutions for m > –1 one solution for m = –1 no solution for m < –1.
Check Yourself 34
1. |
Solve loga x+ log a x+ log 3 a2 x= 27 for x in terms of a. |
|
||||||
2. |
Determine the number of solutions to |
6 log2 x – log22 x – 8 a for different values of a. |
||||||
Answers |
|
|
|
|
|
|
|
|
|
|
|
if |
a or a =1 |
|
no solution |
if |
a>1 |
1. |
|
2. |
one solution |
if |
a=1 |
|||
S = |
} |
if |
a > 0 and a 1 |
|||||
|
{a6 |
|
|
|
|
|||
|
|
|
|
|
|
|
if |
a<1 |
|
|
|
|
|
|
two solutions |
||
210 |
Algebra 11 |
2. Logarithmic Inequalities
Sometimes we are asked to solve inequalities between two functions of the form logf(x)g(x)
and logf(x)h(x), for example: logf(x)g(x) > logf(x)h(x), logf(x)g(x) logf(x)h(x), etc. In this case we can establish the systems
f(x) 1 |
or |
0 f(x) 1 |
to respect the monotone property of logarithmic |
|
g(x) h(x) |
g(x) h(x) |
|||
functions and combine them with the existence conditions |
||||
f(x) 0, f(x) 1 |
|
|
||
g(x) 0 |
|
|
|
|
h(x) 0. |
|
|
|
|
As a result, we get |
|
|
|
|
f(x) 1 |
|
f(x) 0 |
|
|
|
f(x) 1 |
|
||
g(x) h(x) |
and |
as possible systems for the inequality. |
||
g(x) h(x) |
||||
g(x) 0 |
|
h(x) 0 |
|
|
|
|
|
||
We can solve the resulting systems using a sign table. The values satisfying any of these systems will be included in the solution set of the original inequality.
For logarithmic inequalities which do not have functions of the form logf(x) g(x) and logf(x) h(x), we first apply the properties of logarithms in order to write them in this form.
Let us look at some examples.
EXAMPLE 100 Solve the inequalities.
a. log3(3 – x) log3(x + 5)
c.log2(x2 + 4x + 3) 3 e. log(x2 – 5x + 7) 0
b. |
log 1 |
(x – 2) log 1 |
(1– 2 x) |
|||
|
5 |
|
|
|
5 |
|
d. |
log 1 |
|
x – 3 |
– |
1 |
|
|
x+3 |
2 |
|
|||
|
4 |
|
|
|
||
|
|
|
|
|
|
|
f. log2x(5x – 3) 1
Solution a. Using the monotone property of logarithmic functions and the existence conditions for
logarithms, we obtain the system |
|
|
|
|||
3 |
– x x + 5 |
|
–1 x |
|
|
|
|
|
x (–1, 3) |
. |
|||
3 |
– x 0 |
|
3 x |
|
|
|
|
|
|
|
|||
b. Since the base is between zero and 1, we establish the system
x – 2 1 – 2x |
x 1 |
|
x – 2 0 |
|
x > 2 , which has no solution. |
|
|
1 |
1 – 2x > 0 |
> x |
2 |
Exponential and Logarithmic Functions |
211 |

c.The right-hand side of the inequality is not in logarithmic form. However, we can use the identity log2 2 = 1 and write
log |
(x2 |
+ 4x + 3) 3 log 2 log (x2 + 4x + 3) log |
23. |
||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
2 |
|
||
Since the base is greater than 1, this inequality is equivalent to |
|||||||||||||||||||||||
|
x2 + 4x + 3 23 |
|
(x + 5) (x – 1) 0 |
|
x [–5, 1] |
||||||||||||||||||
|
x2 + 4x + 3 0 |
|
|
(x + 3) (x + 1) 0 |
|
x (– , –3) (–1, ). |
|||||||||||||||||
So the common solution is x [–5, –3) (–1, 1]. |
|
|
|
|
|||||||||||||||||||
d. Using a similar approach, we can write |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
x – 3 |
|
1 |
|
|
|
|
x – 3 |
|
1 |
– |
1 |
|
|
x – 3 |
|
|
||||
log 1 |
– |
log 1 |
log 1 |
2 |
log 1 |
log 1 2. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2 |
|
|
x+3 |
|||||||||||||||||
|
4 x+3 |
|
|
|
|
4 x+3 |
4 |
4 |
|
|
|
4 |
|
4 |
|||||||||
Therefore we solve the system |
|
|
|
|
|
|
|
|
|
||||||||||||||
x – 3 |
2 |
|
–x – 9 |
0 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x+3 |
|
|
|
|
|
|
|
|
|
|
||||||||
x+3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x – 3 |
0 |
|
x – 3 |
0. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x+3 |
|
|
|
x+3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
By considering the critical values, we establish the sign table:
|
x |
–¥ |
–9 |
–3 |
3 |
¥ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
x – 3 |
+ |
|
+ |
|
– |
|
+ |
|
|
|
|
|
|
|
|
|
||||
|
x + 3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
–x – 9 |
– |
|
+ |
|
– |
|
– |
|
|
|
|
|
|
|
|
|
||||
|
x + 3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Common |
|
|
|
|
|
|
|
|
||
solution |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Therefore the solution is x (– , –9] (3, ).
Note
For inequalities of the form loga g(x) > b or logag(x) < b, we can use the property b = loga ab and write
for a > 1: loga g(x) b 0 g(x)b ab loga g(x) b g(x) a ,
loga g(x) b g(x) ab loga g(x) b 0 g(x) ab.
e.We have log(x2 – 5x + 7) 0 log(x2 – 5x + 7) log 1. Establishing the appropriate system, we get
x2 |
–5x + 7 1 |
|
x2 – 5x + 6 0 |
|
(x – 2)(x – 3) 0 |
x (2, 3). |
|
x2 |
– 5x + 7 0 |
x |
x |
||||
|
|
|
212 |
Algebra 11 |

 f. By the properties of logarithms, we can write the inequality as log2x(5x – 3) 1 log2x(5x – 3) log2x(2x).
f. By the properties of logarithms, we can write the inequality as log2x(5x – 3) 1 log2x(5x – 3) log2x(2x).
loga a =1
There are two cases: the base may be between zero and 1, or it may be greater than 1. Accordingly we have the two systems
|
|
|
|
|
0 <2x <1 |
|
and |
2x >1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
5x – 3 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
5x – 3 2x |
|
|
|
5x – 3 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
The first system has no solution, because we obtain |
0 < x < |
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
2 , which is impossible. |
|
|||||||||||||||||||||||||||||||
|
For the second system, we have |
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
x > |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 , 1]. So this is the solution to the inequality. |
|||||||||||||||
|
|
|
|
|
x 1 |
|
, which has the solution |
x ( |
|||||||||||||||||||||||||||||
|
|
|
|
|
x > |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
101 Solve the inequalities. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
EXAMPLE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
a. log 1 |
|
|
|
x2 |
+ x |
|
|
|
|
|
|
b. (logx 2 log2x |
2) > log4x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
log6 |
|
|
|
|
|
|
|
< 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x+4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Solution a. We establish the system |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
log |
|
x2 + x |
>1 |
|
x2 + x |
> 6 |
|
x2 + x |
– 6 > 0 |
|
|
|
x2 – 5x – 24 |
> 0 |
|
|
|
|||||||||||||||
|
|
|
|
|
6 |
|
x+4 |
|
|
|
x+4 |
|
x+4 |
|
|
x+4 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x2 + x |
> 0 |
|
|
|
|
x2 + x |
> 0 |
|
x2 + x |
> 0 |
|
|
|
|
x2 + x |
> 0. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
x+4 |
|
|
|
|
x+4 |
|
x+4 |
|
|
|
|
x+4 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Considering the critical values –4, –3, 8 for |
x2 – 5x – 24 |
, |
and –4, –1, 0 for |
|
x2 + x |
, |
we |
|||||||||||||||||||||||||||||
|
|
x+4 |
|
x+4 |
|||||||||||||||||||||||||||||||||
|
establish the following sign table: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
–¥ |
|
|
|
|
–4 |
|
–3 |
|
–1 |
|
|
0 |
|
|
8 |
|
¥ |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x2 – 5x – 24 |
|
|
|
|
|
|
– |
|
|
+ |
|
|
– |
|
|
– |
|
|
|
– |
|
|
+ |
|
|
|
||||||||
|
|
|
|
x + 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x2 + x |
|
|
|
|
|
|
|
– |
|
|
+ |
|
|
+ |
|
|
– |
|
|
|
+ |
|
|
+ |
|
|
|
||||||
|
|
|
|
x + 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Common |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
solution |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Therefore the solution is x (–4, –3) (8, ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Exponential and Logarithmic Functions |
213 |

b. Using the rule loga b = |
|
|
1 |
|
, we get |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
logb a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
( |
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|||||||
|
|
( |
|
. |
|
)> |
|
|
. |
|
|
)> |
|
|
. |
|
||||||||||||||||||||
|
|
log2 x |
log2 2x |
log 2 4x |
log 2 x |
1+ log 2 x |
2+ log 2 x |
|
||||||||||||||||||||||||||||
Substituting y for log2 x, we get |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
1 |
|
|
> |
1 |
|
|
|
|
|
1 |
|
– |
1 |
|
> 0 |
|
|
|
–y2 +2 |
> 0. |
|
|
|||||||||||||
|
|
|
y (y+1) |
y+2 |
y (y+1) |
y+2 |
y (y+1) (y+2) |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
We can establish the corresponding sign table as |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
y |
–¥ |
|
|
|
|
–2 |
|
|
|
–ñ2 |
|
|
|
|
–1 |
|
0 |
ñ2 |
¥ |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–y2 + 2 |
|
|
|
|
|
|
+ |
|
|
|
– |
|
|
|
|
|
|
+ |
|
|
|
|
– |
|
+ |
|
– |
|||||||
|
y × (y + 1) × (y + 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
which leads us to the solution y (– , –2) (–ñ2, –1) (0, ñ2).
We can find the corresponding values of x by considering the three cases: For y (– , –2), y = log2 x –2 0 x 2–2 0 x 14 .
For y (–ñ2, –1), |
–ñ2 log |
|
x –1 2–ñ2 |
x 2–1 |
|
< x < 1 . |
2 |
|
|||||
|
|
|
|
2 2 |
2 |
|
|
|
|
|
|
For y (0, ñ2), 0 log2 x ñ2 1 x 2ñ2.
Therefore the solution is x (0, 14 ) ( 212 , 21 ) (1, 2ñ2).
Check Yourself 35
Solve the inequalities.
a. log3(1 – 2x) log3(5x – 2)
c. log2(2x – 1) 0
e.log2(x+1) < 0 x+1
g. 1– 2 log 1(x+1) log 3( x– 3)
|
|
9 |
|
|
Answers |
|
|
|
|
a. |
x (2 , |
3) |
b. |
x (0, log3 2) |
|
5 |
7 |
|
|
e. |
x (–1, |
0) |
f. |
x (14, ) |
b. log 1 (3x+1 – 3)> log 1(3x +1)
22
d.log 1 (5x – 1) 0
3
f. 2 log8(x – 2) – log8(x + 4) > 1
h. logx+1(3x – 1) > 1
c. |
x (1, ) |
d. |
x ( |
1 |
, |
2 |
] |
|
|
|
|
5 |
|
5 |
|
g. |
x (3, ) |
h. x (–1, |
0) (1, ) |
||||
214 |
Algebra 11 |

C. SYSTEMS OF EQUATIONS AND INEQUALITIES
1. Systems of Equations
We can solve systems of exponential or logarithmic equations by using the properties we have studied so far combined with algebraic operations, elimination and substitution. We write the solution of a system as a set of ordered pairs, triples or quadruples, etc. depending on the number of unknowns in the system.
|
102 |
|
3x + 3y = 28 |
|
2x 3y = 12 |
EXAMPLE |
|
|
|||
|
Solve the systems of equations. |
|
|
||
|
|
a. |
3x+y = 27 |
b. |
2y 3x = 18 |
|
|
|
|
||
Solution |
a. Substituting 3x = a > 0 and 3y = b > 0, we have |
||||
|
|
|
a + b = 28 |
|
a = 28 – b |
|
|
|
a b = 27 (3x+y = 3x 3y) |
|
a b = 27 |
xy+1 = 27
c.x2y–5 = 13
a = 28 – b |
|
(28 – b) b = 27 |
a = 28 – b |
a = 28 – b |
|
a = 28 – b |
|
b2 – 28b + 27 = 0 |
(b – 27) (b – 1) = 0 |
b = 1 or b = 27. |
|
|
|
b = 1 |
b = 27 |
3x = 1 |
3x = 27 |
So the solutions for a and b are |
a = 27 or |
a = 1 , which give us 3y = 27 and |
3y = 1 . |
|
Hence the possible cases are |
x = 0 or |
x = 3 . |
|
|
|
y = 3 |
y = 0 |
|
|
So the solution is {(0, 3), (3, 0)}. |
|
|
|
|
|
|
|
b. We begin by multiplying the second equation by the first: |
|
|
|
|
|||
2x 3y = 12 |
|
2x 3y = 12 |
|
2x 3y = 12 |
|
2x 3y = 12 |
|
2x 3y 2y 3x = 12 18 |
|
2x+y 3x+y = 216 |
|
6x+y = 63 |
|
x + y = 3 |
|
2 |
x |
3 |
3 – x |
= 12 |
|
|
x |
|
27 |
2 x 2 2 |
|
|
|
2 |
|
3x =12 |
( 3) =( 3) |
||||
y = 3 – x |
|
y = |
3 – x |
y = 3 – x |
||||||
|
|
|
|
|
|
|||||
So {(2, 1)} is the solution.
c. Taking the square of the first equation, we have
x = 2 y = 1.
(xy+1 )2 =(27)2 |
x |
2y |
|
2 |
6 |
3 |
–1 |
|
5 |
2 |
|
6 |
||
|
|
|
x = 3 |
|
|
x |
x = 3 |
|
||||||
x2y– 5 = 1 |
x2y x–5 = 3–1 |
x2y = 3–1 x5 |
|
|||||||||||
|
||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x7 = 37 |
|
x = 3 |
|
|
x = 3 |
|
x = 3 |
|||||||
x2y = 3–1 x5 |
32y = 3–1 35 |
32y = 34 |
y = 2. |
|||||||||||
Hence {(3, 2)} is the solution.
Exponential and Logarithmic Functions |
215 |

EXAMPLE 103 Solve the systems of equations.
|
x + y = 7 |
|
|
|
|
|
|
|
|
|
|
|
|
1 – |
1 |
= |
2 |
|
|
||
a. |
|
|
|
|
|
|
|
|
|
|
b. |
y |
|
|
|
||||||
ln x + ln y = 2 ln 2 + ln 3 |
|
|
|
|
|
|
|
x |
15 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
log3 |
x+ log3 |
y=1+ log 3 5 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Solution a. We can use the properties of logarithms to write |
|
|
|
|
|
|
|
|
|||||||||||||
|
ln x + ln y = 2 ln 2 + ln 3 ln (x y) = ln (22 3) x y = 12. |
||||||||||||||||||||
|
So we just need to solve the system |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x + y = 7 |
y = 7 – x |
|
|
|
|
y = 7 – x |
|
|
|
y = 7 – x |
||||||||||
|
x y = 12 |
x (7 – x) = 12 |
|
x2 – 7x + 12 = 0 |
x = 3 or x = 4. |
||||||||||||||||
|
Hence the solution is {(4, 3), (3, 4)}. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Notice that both pairs satisfy the existence conditions for logarithms. |
|
|||||||||||||||||||
b. Using a similar approach, we can work on the second equation in the system to get |
|||||||||||||||||||||
|
log3 x + log3 y = 1 + log3 5 log3(x y) = log3(3 5) x y = 15. |
||||||||||||||||||||
|
So we have the system |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
1 |
2 |
|
1 |
x 2 |
|
15 – x2 |
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
– y = |
|
|
x – 15 = 15 |
|
15x = |
15 |
|
|
|||||||||||
|
x |
15 |
|
|
|
||||||||||||||||
|
x y =15 |
y = |
15 |
|
|
|
|
y = 15. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x2 +2x – 15 = 0 |
|
x = –5 or x= 3 |
x = –5 |
or |
x = 3 |
|||||||||||||||
|
|
|
15 |
|
|
|
|
15 |
|
|
|
||||||||||
|
y = |
|
|
|
y = |
|
|
|
y = –3 |
|
|
|
y = 5 |
||||||||
|
x |
|
|
|
|
x |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
To satisfy the existence conditions, x and y must be positive. Therefore we eliminate the case x = –5 and write the solution as {(3, 5)}.
Check Yourself 36
Solve the systems of equations. 3x + 3y = 4
x + y = 1
5x+4y = 7
ln x+ ln y = ln( 53)
8 c. logy x – log x y= 3
x =16y
2x 3y |
= 36 |
2x 3y = 24 |
b. |
|
c. |
2x + 3y = 13 |
2y 3x = 54 |
|
4x2 – y2 = 2
b.
log2(2x + y) – log2(2x – y) = 1
y xlogy x = x2ñx
d.
log3 y logy(y – 2x) = 1
Answers |
|
|
|
|
|
|
|
|
|
|
|
|
1. |
a. {(0, 1), (1, 0)} |
b. {(log2 9, log3 4), (2, 2)} |
|
c. {(3, 1)} |
|
|||||||
2. |
a. {( 4 , |
3), ( |
3 |
, 1)} |
b. {( |
3 |
, |
1)} |
c. |
{(2, |
1), (64, 4)} |
d. {(3, 9)} |
|
5 |
4 |
5 |
|
|
4 |
|
2 |
|
|
8 |
|
216 |
Algebra 11 |
2. Systems of Inequalities
To solve a system of exponential or logarithmic inequalities, we consider each inequality separately and find its solution. Then we add the existence conditions of logarithms to the system and find a common solution set. We can also use a sign table to look at the different cases.
The following examples illustrate this approach.
EXAMPLE 104 Solve the systems of inequalities.
|
|
1 |
– x |
|
|
|
|
|
3 |
2x+1 |
– 3 |
x+2 |
+ 6 |
0 |
|
a. (8) |
|
<128 |
|
|
b. |
|
|
||||||
|
|
24x |
16 |
|
|
|
|
32x+2 – (2 3x+2) – 27 0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Solution |
a. |
23x < 27 |
|
3x < 7 |
|
x < |
7 |
|
|
|
|
|
||
24x |
24 |
4x 4 |
3 |
|
|
|
|
|
||||||
|
|
|
|
x 1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Hence the solution set is S = (– , |
7 ) [1, ) = [1, |
7 ). |
||
|
|
|
3 |
3 |
b. Using the rules of exponents, we get |
|
|||
32x+1 – 3x+2 + 6 > 0 |
|
(3 (3x)2) – 9 3x + 6 > 0 |
||
32x+2 – (2 3x+2) – 27<0 |
(9 (3x)2) – (18 3x) – 27 < 0 |
|||
Let us find the critical values and establish a sign table: |
||||
3x – 2 = 0 |
3x = 2 |
x = log3 2 |
|
|
3x – 1 = 0 |
3x = 1 x = 0 |
|
||
3x – 3 = 0 |
3x = 3 x = 1 |
|
||
3x + 1 > 0, so there is no critical value here. |
|
|||
3 (3x – 2) (3x – 1) > 0 9 (3x – 3) (3x + 1) < 0.
x |
–¥ |
0 |
log3 2 |
1 |
¥ |
||||
32x+1 – 3x+2 + 6 |
|
+ |
|
– |
|
+ |
|
+ |
|
32x+2 – (2 × 3x+2) – 27 |
|
– |
|
– |
|
– |
|
+ |
|
Common |
|
|
|
|
|
|
|
|
|
solution |
|
|
|
|
|
|
|
|
|
In conclusion, the solution set is S = (– , 0) (log3 2, 1).
EXAMPLE 105 Solve the systems of inequalities.
a. |
log2 |
(3 – x)< 2 |
b. |
log 1 |
x+2 log 1 |
(x – 1) |
log 1 |
6 |
log 1 |
(x+2)< 0 |
3 |
9 |
|
3 |
|
||
|
|
log2 |
(x+1)<1– 2 log 4 x |
|
||||
|
3 |
|
|
|
||||
Exponential and Logarithmic Functions |
217 |

Solution a. Adding the existence conditions, the system becomes
log2 |
(3 – x)< 2 |
|
3 – x < 22 |
|
–1 < x |
|
log 1 |
(x+2)< 0 |
|
x+2 >( |
1 |
0 |
x > –1 |
3 |
|
|
3 |
) |
|
|
3 – x > 0 |
|
|
|
3 > x |
||
|
3> x |
|
|
|||
x+2 > 0 |
|
|
|
|
||
|
x > –2 |
|
|
x > –2. |
||
|
|
|
|
|
||
Hence the common solution is {(–1, 3)}.
b. By working on the logarithmic expressions and introducing the existence conditions, we get
log 1 |
x+2 log |
1 |
2 (x – 1) |
3 |
( |
3 ) |
|
log2(x+1)<1– 2 log 22 x x > 0
x – 1> 0 x+1> 0
log 1 |
[x (x – 1)] |
log 1 |
6 |
3 |
|
3 |
|
log2[(x+1) x]< log 22 x >1
(x – 3)(x + 2) 0
(x + 2)(x – 1) < 0 x > 1
log 1 6 |
log 1 |
x+ log 1(x – 1) log 1 6 |
|
3 |
3 |
3 |
3 |
|
log2 |
(x+1)+ log 2 |
x<1 |
|
x > 0 |
|
|
|
|
||
|
x >1 |
|
|
|
x > –1 |
|
|
x2 – x 6 |
x2 – x – 6 0 |
||
x2 + x < 2 x2 + x – 2 < 0 |
|||
x > 1 |
|
x > 1 |
|
x –2 or x 3 –2 < x < 1
x > 1.
Since there is no common solution for these intervals, we conclude that the system has no solution.
Check Yourself 37
Solve each system of inequalities.
|
|
32x |
243 |
|
2 |
x |
+ 2 |
x+1 |
+ 2 |
x+2 |
28 |
|
|
9x – 3x+2 < 3x – 2 – 1 |
|||||
1. a. |
|
1 |
|
|
b. |
|
|
|
|
c. |
|||||||||
|
2x |
|
|
x+1 |
|
|
x |
|
|
|
|
||||||||
|
|
(9) |
< 27 |
|
5 |
|
|
+ 5 |
|
< 750 |
|
|
|
|
x3 + 2x 3 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
log |
3 |
2x+1 <1 |
|
|
|
|
log3(2x+1)< 2 |
|
|
|
|
|
|
b. |
|
x+1 |
|
|||||||
2. a. |
|
|
|
|
|
|
|
|
|
x – 3 |
1 |
||||||||
|
log 1 (3x – 1) 1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
log 1 |
|
< – |
|
||||||
|
|
|
|
|
|
|
|
|
|
x+3 |
2 |
||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
Answers |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1. a. (– |
3 |
, |
5] |
|
b. [2, 3) |
|
|
|
c. [1, 2) |
|
|
|
|
|
|
||||
|
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. a. ( |
1 |
, |
4] |
|
b. (–9, –3) |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
218 |
Algebra 11 |
