6.9. Потенціальна енергія при крученні. Аналіз напруженого стану при крученні

При пружній деформації потенціальна енергія деформації , що накопичується у валі, чисельно дорівнює роботі зовнішніх сил:

. (6.37)

Робота зовнішніх сил при крученні дорівнює:

, (6.38)

де  крутний момент, викликаний дією зовнішнього моменту .

Підставляючи значення для роботи зовнішніх сил у формулу (6.37) і з огляду на те, що, одержимо:

. (6.39)

Формулою (6.39) можна користуватися при східчастій зміні крутних моментів і жорсткості вала. Потенціальна енергія в цьому випадку дорівнюватиме сумі потенціальних енергій, знайдених на кожній ділянці зі сталим відношенням .

Як випливає з виразів (6.27) і (6.31), а також з рис.6.14, дотичні напруження, змінюючись за величиною уздовж радіуса, залишаються йому перпендикулярні. На підставі закону парності дотичних напружень вони виникають також і в поздовжніх перерізах (Рис.6.15).

Рис.6.15

Нормальні напруження як у поперечних, так і в поздовжніх перерізах дорівнюють нулю. Уздовж радіуса дотичні напруження також відсутні. Таким чином, на двох взаємно перпендикулярних площадках, одна з яких лежить у площині поперечного перерізу, а інша у площині поздовжнього діаметрального перерізу, діють тільки дотичні напруження. Такий напружений стан називається чистим зсувом. Як відомо, при чистому зсуві в площадках, які нахилені до площадок чистого зсуву під кутом 45⁰ (у данному випадку під кутом 45⁰ до осі вала), діють головні розтягальні і стискальні нормальні напруження. Траєкторія цих напружень являє собою гвинтову лінію, нахилену під кутом 45⁰ до утворюючої (Рис.6.16).

Рис.6.16

За величиною головні напруження іу всіх точках перерізу дорівнюють дотичним напруженням. Подібна дія нормальних напружень викликає руйнування матеріалів, що знаходяться у крихкому стані, по гвинтовій лінії, тому що крихкі матеріали не задовільно чинять опір розтяганню.

6.10. Умови міцності і жорсткості при крученні валів. Приклади розрахунку валів

Розрахунок валів на міцність, як правило, виконують за допустимими напруженнями. Умова міцності має вигляд:

. (6.40)

Допустимі напруження , визначається відповідно до методики, викладеної в розділі 6.7 даної теми.

Умова міцності (6.40) дозволяє вирішувати три задачі:

1. Перша задача полягає у перевірці напружень при заданому моменті і відомому діаметрі вала.

2. Друга задача полягає у визначенні допустимої величини для моменту при заданому діаметрі вала і відомому допустимому напруженні.

3. Третя задача є задачею проектувального розрахунку: при заданому моменті і допустимому напруженні необхідно знайти діаметр вала.

Перш, ніж перейти до розв’язання третьої задачі, запишемо формули, у яких полярний момент інерції і полярний момент опору виражені через діаметр вала.

Полярний момент інерції для суцільного перерізу вала був визначений у темі №5, формула (5.15):

.

Для порожнистого вала (кільцевий переріз) з зовнішнім діаметром і внутрішнім:

,

де

.

Полярний момент опору для суцільного перерізу знайдемо за формулою:

.

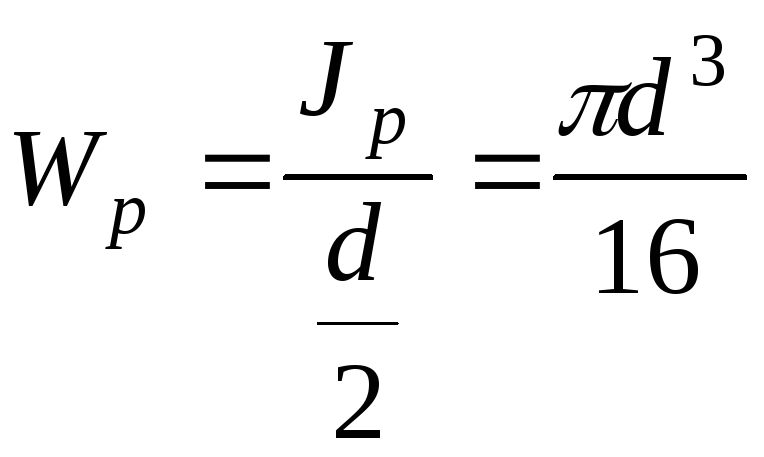Для кільцевого перерізу полярний момент опору дорівнюватиме:

.

Тепер діаметр суцільного вала може бути знайдений з умови міцності таким чином:

, звідки .

Для вала кільцевого перерізу:

, звідки .

Крім розрахунку на міцність, вали розраховують також на жорсткість. Умова жорсткості має вигляд:

, (6.41).

де  відносний кут закручування;  відносний допустимий кут закручування вала в рад/м, нормований технічними умовами.

Діаметр суцільного вала з умови жорсткості (6.41) при дорівнюватиме:

.

Для кільцевого перерізу . Тому

.

Таким чином, діаметр вала визначається двічі: один раз – з умови міцності, другий  з умови жорсткості. З двох отриманих розмірів береться більший.

Величина зовнішнього моменту не завжди задається безпосередньо. Часто доводиться визначати момент за числом обертів вала за хвилинуі потужністю машини, що обертає вал, вираженій в кінських силах або в кіловатах.

Потужність являє собою роботу в одиницю часу (секунду), яка дорівнює роботі зовнішнього моменту , де кут, на який повернеться шків за одну секунду.

За одну секунду шків зробить обертів, отже,. Роботу на цьому куті повороту знайдемо з формули:

(кНм/с).

З іншого боку

(кНм/с),

де  потужність у кінських силах.

Дорівнюючи ці два вирази, знайдемо:

(кНм). (6.42)

З огляду на те, що одна кінська сила дорівнює 0,736кВт і виражаючи зовнішній момент через потужність , задану в кіловатах, одержимо:

(кНм). (6.43)

Приклад 6.2. Стержень круглого поперечного перерізу довжиною см і діаметромсм скручується моментомкНм.

Визначити:

1. Дотичне напруження у точці поперечного перерізу стержня, що відстоїть на відстані 1 см від центра ваги перерізу.

2. Знайти максимальний кут закручування стержня. Матеріал стержня – сталь (МПа).

Розв’язок:

1. Крутний момент у валі дорівнюватиме зовнішньому моментові

кНм.

2. Дотичне напруження в будь-якій довільній точці перерізу вала можна визначити за формулою (6.31):

МПа.

3. Максимальний кут закручування вала знайдемо за формулою (6.34):

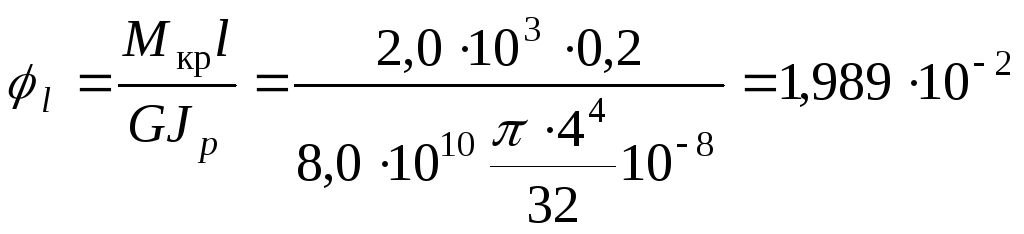рад.

Приклад 6.3. Вал скручується моментом кНм. Допустиме напруження дорівнюєМПа. Допустимий кут закручування дорівнюєрад/м. Модуль зсувуМПа. Визначити діаметр вала.

Розв’язок:

1. З умови міцності (6.40) знаходимо:

ммм.

3. З умови жорсткості (6.36):

ммм.

4. З двох отриманих діаметрів беремо більший, тобто

мм.

Приклад 6.4. Визначити діаметр вала кільцевого перерізу, якщо потужність, що передається валом, дорівнює кВт. Кількість обертів вала за хвилину. Допустиме напруження дорівнюєМПа. Допустимий кут закручування дорівнює(м^-1). Модуль зсуву МПа. Відношення діаметрів.

Розв’язок:

1. Момент, що передається на вал, визначаємо за формулою (6.43):

(кНм).

2. Визначаємо діаметр з умови міцності:

ммм.

5. Знаходимо діаметр 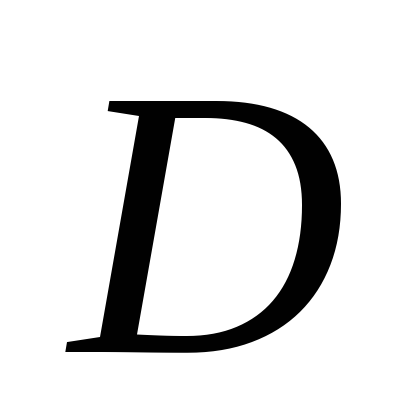з умови жорсткості:

ммм.

5. Беремо більше значення для діаметра вала: мм;мм.

Приклад 6.5. Як відрізняється несуча здатність двох валів при крученні (Рис.6.17), якщо для першого вала МПа, а для другого МПа.

Рис.6.17

Розв’язок:

1. З умови міцності (6.40) знайдемо величину крутного моменту для першого перерізу:

Нм.

2. З умови міцності знайдемо величину крутного моменту для другого перерізу:

Нм.

3. Порівнюючи моменти для першого і другого перерізу, дістаємо висновку, що у другого перерізу несуча здатність у 1,9 разів більша:

.

Приклад 6.6. Як відрізняються жорсткості двох валів при крученні (Рис.6.17), якщо для першого вала модуль пружності МПа, а для другого МПа.

Розв’язок:

1. Знаходимо жорсткість для першого перерізу:

(Нм²).

2. Знаходимо жорсткість для другого перерізу:

(Нм²).

3. Порівнюючи жорсткості для першого і другого перерізів, дістаємо висновку, що у другого перерізу жорсткість у 8,43 разів більша:

.