Тема 6 определение перемещений при изгибе. Расчет балок на жесткость

6.1. Понятие об упругой линии. Прогиб и угол поворота. Дифференциальное уравнение упругой линии. Условие жесткости при изгибе

Чтобы судить о работе изгибаемых балок, недостаточно знать только напряжения, которые возникают в сечениях балки от заданной нагрузки. Вычисленные напряжения позволяют проверить прочность системы. Однако весьма прочные балки могут оказаться непригодными к эксплуатации из-за недостаточной жесткости. Если балка при нагружении сильно прогибается, то при эксплуатации сооружения, имеющего гибкие балки, появятся затруднения и, кроме того, могут возникнуть колебания балки с большими амплитудами, а вместе с тем и значительные дополнительные напряжения.

Под жесткостью следует понимать способность элеменов конструкций и деталей машин сопротивляться внешним нагрузкам без видимых деформаций. Расчет на жесткость заключается в оценке упругой податливости балки под действием приложенных нагрузок и подбор таких размеров поперечного сечения, при которых перемещения не будут превышать установленных нормами пределов. Для выполнения такого расчета необходимо научиться вычислять перемещения сечений балки под действием любой внешней нагрузки.

Рассмотрим деформацию балки при простом изгибе. Ось балки (Рис.6.1,а) под действием нагрузки, расположенной в одной из главных плоскостей инерции (в плоскости ), искривляется в той же плоскости, а поперечные сечения поворачиваются и одновременно получают поступательные перемещения. Искривленная ось балки называетсяизогнутой осью или упругой линией. На рис. 6.1 упругая линия изображена тонкой кривой.

Точка , лежащая на оси в сечении, отстоящем не расстоянииот начала координат, переместится в точку. Обозначим перемещение произвольной точки оси бруса в направлении осичерез, а перемещение вдоль оси бруса – через. Если в точкепровести касательную к оси изогнутой балки, то по отношению к первоначальному положению оси она будет повернута на угол. Одновременно на тот же угол повернется сечение в точке. Таким образом, три величины ,иявляются компонентами перемещения произвольного поперечного сечения балки. Перемещениецентра тяжести сечения по направлению, перпендикулярному к оси балки, называетсяпрогибом. Наибольший прогиб называется стрелой прогиба и обозначается буквой .

Угол , на который каждое сечение поворачивается по отношению к своему первоначальному положению, называется углом поворота сечения. Как уже отмечалось, угол поворота также может быть определен как угол между касательной к упругой линии и осью.

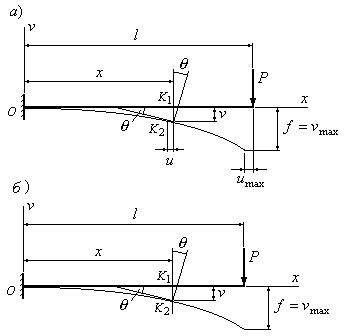
Рис.6.1

Проверка жесткости балок сводится к требованию, в соответствии с которым наибольший прогиб не должен превышать определенной доли пролета:

.

Число устанавливается нормами проектирования примерно в пределах от 300 до 1000. Для ответственных сооружений, например, для железнодорожных мостов, величинапринимается равной 1000.

Отсюда видно, что прогибы при изгибе, как правило, малы по сравнению с пролетом балки. Это позволяет внести некоторые упрощения. Во-первых, при малых прогибах угол наклона касательной к оси изогнутой балки можно определять с помощью выражения:

. (6.1)

Во-вторых, горизонтальными перемещениями можно пренебречь, так как они существенно меньше(). В связи с этим при расчетах будем пользоваться условной схемой перемещений, изображенной на рис 6.1,б. Согласно этой схеме каждая точка перемещается перпендикулярно продольной оси бруса.

Для определения полной картины деформаций необходимо получить уравнение упругой линии

.

Исходя из физической природы изогнутой оси бруса, можем утверждать, что упругая линия должна быть непрерывной и гладкой кривой, следовательно, на протяжении всей оси бруса должны быть непрерывны функция и ее первая производная. Прогибы и углы поворота и являются перемещениями сечений балок при изгибе. Деформация того или иного участка балки определяется его кривизной.

При выводе формулы для нормальных напряжений при изгибе нами была получена связь между кривизной и изгибающим моментом:

. (6.2)

Из курса высшей математики известно следующее уравнение кривизны плоской кривой:

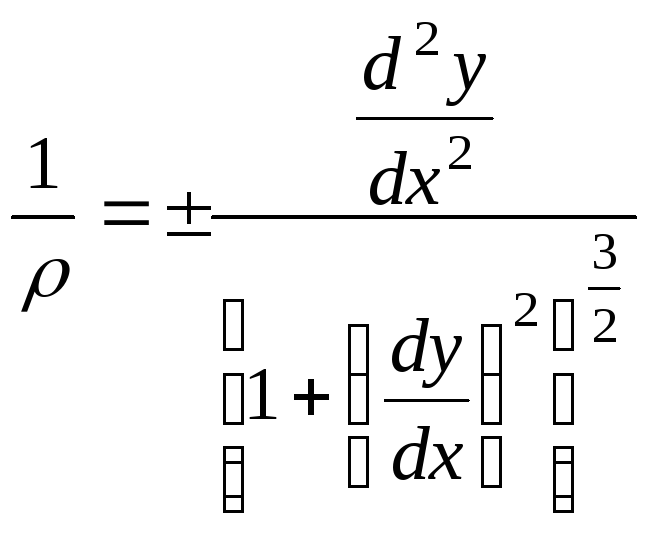. (6.3)

Подставляя значение кривизны в равенство (6.2) и заменяя координату прогибом, получим точное дифференциальное уравнение упругой линии балки:

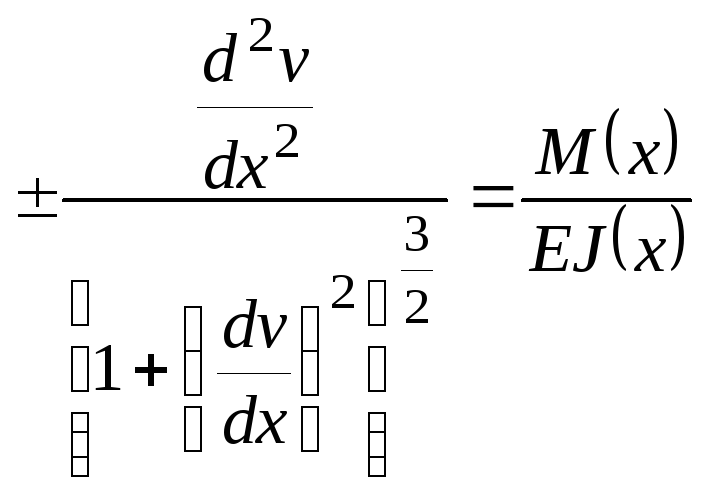. (6.4)

Интегрирование этого нелинейного дифференциального уравнения связано с большими трудностями. Учитывая, что на практике приходится иметь дело с малыми прогибами и что тангенсы углов наклона касательной к оси будут малы, квадратом первой производнойпо сравнению с единицей можно пренебречь. Тогда получим приближенное (основное) дифференциальное уравнение

(6.5)

Два знака в уравнении (6.5) поставлены потому, что знак кривизны может не совпадать со знаком изгибающего момента. Знак кривизны зависит от направления осей координат. Знак изгибающего момента был выбран в зависимости от того, где расположены растянутые волокна. Так, например, для случая, когда осьнаправлена вверх, положительному моменту (Рис.6.2,а) соответствует положительная кривизна, а отрицательному – отрицательная кривизна.

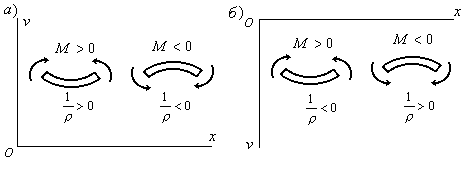
Рис 6.2

Таким образом, в случае, когда ось направлена вверх, знаки кривизны и изгибающего момента совпадают. Поэтому в дифференциальном уравнении берется знак“+”. Если ось направлена вниз, то знаки у кривизны и изгибающего момента будут различны (Рис.6.2,б). Поэтому в этом случае в правой части уравнения (6.5) берется знак“”.

6.2. Метод непосредственного интегрирования приближенного (основного) дифференциального уравнения упругой линии

Решая задачу аналитическим методом, углы поворота и прогибывычисляют последовательным интегрированием приближенного дифференциального уравнения (6.5). Проинтегрировав уравнение (6.5) первый раз, получим выражение для угла поворота:

, (6.6)

где  постоянная интегрирования.

Интегрируя второй раз, получим выражение для прогиба :

, (6.7)

где и постоянные интегрирования.

Для вычисления интегралов, входящих в (6.6) и (6.7), необходимо сначала написать аналитические выражения для изгибающего момента и жесткости. Постоянные интегрирования находятся из граничных условий, которые зависят от условий перемещения границ участков балки.

Рассмотрим несколько примеров применения метода непосредственного интегрирования приближенного уравнения упругой линии балки.

Пример 6.1. Определить стрелу прогиба и угол поворота сечения В балки, изображенной на рис.6.3.

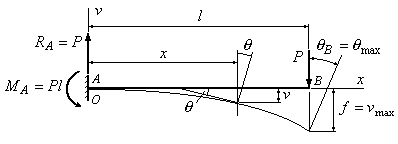
Рис.6.3

Решение:

1. Из условий равновесия определяем опорные реакции:

; .

2. Выбираем начало координат на левом конце балки, совмещая его с точкой А. Осьнаправляем вверх, ось вправо.

3. Составляем уравнение изгибающего момента в сечении :

.

4. Предполагая, что жесткость балки постоянна, записываем приближенное дифференциальное уравнение упругой линии балки:

.

Знак “+” в уравнении упругой лиинии был принят потому, что ось направлена вверх.

5. Интегрируем уравнение первый раз. Получаем:

. (а)

Интегрируя еще раз, получаем уравнение для прогиба в сечении :

. (б)

Так как в заделке прогиб и угол поворота равны нулю, то для определения постоянных интегрирования граничные условия имеют вид:

при ; при.

Из уравнения (а) видно, что постоянная представляет собой угол поворота в начале координат (сечении А). Задавая в уравнении (а), находим. Из уравнения (б) следует, что постоянная прогиб в начале координат. Задавая в уравнении (б) , получаем.

Таким образом, получаем следующие выражения для прогиба и угла поворота:

,

.

Подставляя в первое уравнение , найдем стрелу прогиба:

.

Подставляя во второе уравнение , найдем максимальный угол поворота

.

Знак “” у прогиба свидетельствует о том, что его направление не совпадает с положительным направлением оси . Знак“” в выражении угла поворота показывает, что сечение В повернулось не против, а по часовой стрелке.

Пример 6.2. Определить стрелу прогиба двухопорной балки и углы поворота опорных сечений А и В (рис.6.4).

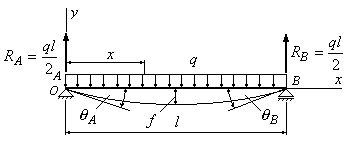
Рис.6.4

Решение:

1. Из условий равновесия определяем опорные реакции:

.

2. Выбираем начало координат на левом конце балки, совмещая его с точкой А. Осьнаправляем вверх, ось вправо.

3. Составляем уравнение изгибающего момента в сечении :

.

4. Предполагая, что жесткость балки постоянна, записываем приближенное дифференциальное уравнение упругой линии балки:

.

Знак “+” в уравнении упругой лиинии был принят потому, что ось направлена вверх.

5. Интегрируем уравнение первый раз. Получим:

. (в)

Интегрируя еще раз, получаем уравнение для прогиба в сечении :

. (г)

Постоянные интегрирования найдем из граничных условий:

при ; при.

Подставляя в уравнение (г) и приравнивая прогиб нулю, получим; подставляя в это же уравнение, находим постоянную интегрирования:

.

Найденные значения постоянных интегрирования подставим в уравнения (в) и (г) и получим уравнения углов поворота и прогибов:

;

.

Подставляя ив первое уравнение, получим углы поворота соответственно сечений А и В:

; .

В силу симметрии нагрузки максимальный прогиб будет посредине балки. Подставляя во второе уравнение , получим:

.

Как и в предыдущем примере, знак “” у прогиба свидетельствует о том, что его направление не совпадает с положительным направлением оси . Знак“” в выражении угла поворота показывает, что сечение А повернулось не против, а по часовой стрелке, знак“+” в выражении угла поворота показывает, что сечение В повернулось против часовой стрелки.

Пример 6.3. В сколько раз прогиб в сечении В на конце изображенной на рис.6.5 балки, больше, чем прогиб в сечении С посредине балки?

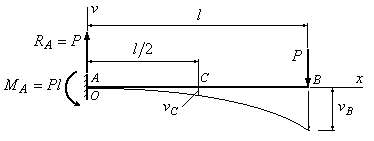
Рис.6.5

Решение:

Воспользуемся результатами, полученными в примере 6.1. Запишем окончательное выражение для прогиба:

и подставим в это уравнение координаты точек С и В. Получим:

при ;

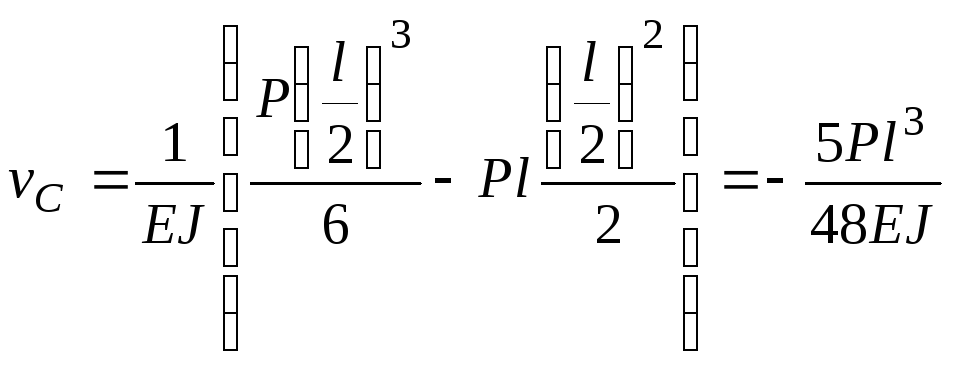при .

Сравнивая полученные величины прогибов, приходим к выводу, что прогиб в сечении В больше, чем прогиб в сечении С в 3,2 раза:

.

Пример 6.4. В сколько раз угол поворота сечения А на конце изображенной на рис.6.6 балки больше, чем угол поворота сечения В на расстоянии четверти пролета от левого конца балки?

Решение:

1. Находим реакции: ;.

2. Выбираем начало координат на правом конце балки, совмещая его с точкой А. Осьнаправляем вверх, ось влево.

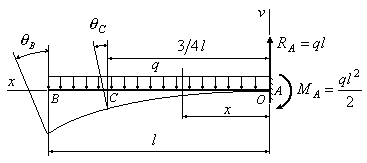
Рис.6.6

3. Записываем выражение для изгибающего момента в сечении :

.

4. Составляем приближенное дифференциальное уравнение упругой линии балки:

.

Знак “+” в уравнении упругой лиинии был принят потому, что ось направлена вверх.

5. Принимаем жесткость балки постоянной. Интегрируем дифференциальное уравнение. Получаем:

.(д)

Постоянную интегрирования в уравнении (д) найдем из условия, что приугол поворота в сечении А равен нулю. Подставим в уравнение (д)и приравняем нулю угол поворота сечения А. Получим. Тогда окончательно уравнение для угла поворота принимает вид:

.(е)

6. Подставляем в уравнение (е) координату , получим угол поворота в сечении С:

.

7. Подставляем в уравнение (е) координату . Получим угол поворота в сечении В:

.

8. Сравнивая углы поворота в сечениях В и С, получим:

.

Таким образом, угол поворота в сечении В в 1,016 раза больше, чем угол поворота в сечении С.

Пример 6.5. Найти стрелу прогиба (в мм) балки, изображенной на рис.6.7, если жесткость поперечного сечения балки равна кНм².

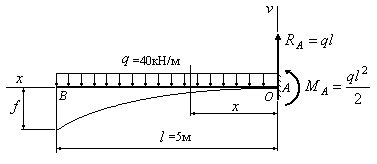
Рис.6.7

Решение:

Воспользуемся решение задачи, ход которого изложен в примере 6.4 и проинтегрируем выражение (д). Получим уравнение для прогиба в сечении :

. (ж)

Постоянные интегрирования в уравнении (ж) получим, воспользовавшись граничными усорвиями закрепления балки, в соответствии с которыми прогиб и угол поворота в жесткой заделке равны нулю:

при и.

Подставляя в уравнения (д) и (ж) и приравнивая последовательно нулю угол поворота и прогиб нулю, получим:;. Тогда выражение для прогиба принимает вид:

.

Подставляя в это уравнение заданные значения жесткости сечения, интенсивности распределенной нагрузки, длину балки, а также координату сечения В, в котором определяется стрела прогиба (), находим:

ммм.

Знак “” у прогиба свидетельствует о том, что его направление не совпадает с положительным направлением оси .