10.8. Теорема Кастільяно. Теорема Лагранжа

Припустимо, що пружна система статично навантажена довільним навантаженням і деякою узагальненою силою(Рис.10.17). Обчислимо потенціальну енергію, накопичену при деформації системи. З цією метою для зручності виберемо наступний порядок навантаження. Спочатку навантажуємо систему силою. Переміщення точки прикладення сили в її напрямку, спричинене цією самою силою, позначимо. Потім прикладаємо навантаження.

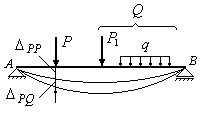
Рис.10.17

Внаслідок додаткової деформації сила дістане переміщення. Повне (узагальнене) переміщення точки прикладення сили:

. (10.42)

Потенціальна енергія деформації, накопичена в системі, буде чисельно дорівнювати роботі зовнішніх сил:

, (10.43)

де  енергія, накопичена внаслідок деформування системи тільки силами , яка чисельно дорівнює роботі силна спричинених ними переміщеннях.

Другий член у формулі (10.43) не містить , оскільки на переміщенні, сила, здійснюючи роботу, не змінювала свого значення. Оскільки, то формулу (10.43) можна записати у вигляді:

. (10.44)

Продиференцюємо вираз (10.44) по силі з урахуванням виразу (10.42):

.

Отже,

. (10.45)

Переміщення точки прикладення узагальненої сили в напрямку її дії дорівнює частинній похідній від потенціальної енергії по цій силі.

Ця теорема названа ім'ям італійського механіка та інженера Карло Альберто Кастільяно (18471884). Ця теорема є однією з основних у будівельній механіці. Виведена спочатку для шарнірних ферм, вона була узагальнена автором на пружне тіло будь-якого виду. У зв'язку з широким впровадженням у розрахункову практику методу Мора спосіб Кастільяно був витиснутий з практики визначення переміщень в стержневих системах. Однак, він залишається загальним методом визначення переміщень в пластинках, оболонках і деталях, усі три виміри яких мають один порядок.

Зазначимо, що відповідно до формули (10.44) друга частинна похідна від потенціальної енергії по узагальненій силі дорівнює:

(10.46)

і завжди додатна.

Для плоскої системи, нехтуючи впливом поздовжньої і поперечної сил, потенціальну енергію запишемо у вигляді:

.

Застосовуючи правило диференціювання по параметру, знаходимо:

. (10.47)

Щоб визначити лінійне або кутове переміщення в перерізі, де за умовою задачі сила відсутня, у цьому перерізі треба прикласти відповідну фіктивну узагальнену силу. Далі, написавши вираз для потенціальної енергії від системи сил, включаючи зазначену фіктивну силу, беруть частинну похідну по цій фіктивній силі та в отриманому виразі для переміщення дорівнюють фіктивне навантаження нулю.

Якщо виразити потенціальну енергію деформації як функцію незалежних узагальнених переміщень , можна показати, щочастинна похідна від потенціальної енергії по будь-якому переміщенню дорівнює відповідній узагальнений силі, тобто:

. (10.48)

Сформульована теорема була встановлена французьким математиком і механіком Жозефом Луї Лагранжем (17361813) і названа його ім'ям.

Розглянемо кілька прикладів застосування теорем Кастільяно і Лагранжа.

Приклад 10.7. Використовуючи теорему Кастільяно, визначити прогин і кут повороту перерізу В для балки, зображеної на рис.10.18, якщо жорсткість поперечного перерізу балки кНм².

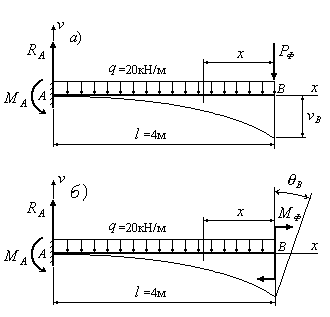
Рис.10.18

Розв’язок:

1. Додамо в перерізі В зосереджену фіктивну силу і запишемо вираз для згинального моменту з урахуванням цієї сили:

. (а)

2. Візьмемо частинну похідну від згинального моменту у виразі (а) по фіктивній силі:

. (б)

3. Підставимо вираз (а) і (б) у формулу (10.47). З огляду на те, що , одержимо:

ммм.

4. Для визначення кута повороту в перерізі В додамо в цьому перерізі фіктивний момент , запишемо вираз для згинального моменту в перерізіз урахуванням цього моменту:

(в)

5. Візьмемо частинну похідну по :

(г)

і підставимо вирази (в) і (г) у формулу (10.47). З огляду на те, що , одержимо кут повороту перерізу В:

рад.

Приклад 10.8. За допомогою теореми Лагранжа визначити величину сили , прикладеної до статично невизначуваної стержневої системи в точці В, якщо переміщення вузла В дорівнюємм (Рис.10.19). Жорсткість поперечного перерізу однакова для всіх стержнів і дорівнюєН. Кут нахилу крайніх стержнів. Довжина крайніх стержнів №1 і №2м. Довжина середнього стержня №3 з урахуванням нахилу крайніх стержнівм.

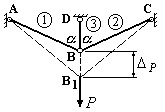
Рис.10.19

Розв’язок:

1. Виразимо деформації стержнів ферми через переміщення вузла В :

; .

2. Виразимо зусилля в стержнях ферми через переміщення вузла В:

; .

3. Обчислимо потенціальну енергію деформації, що накопичується в системі:

.

5. Візьмемо частинну похідну від виразу для потенціальної енергії по 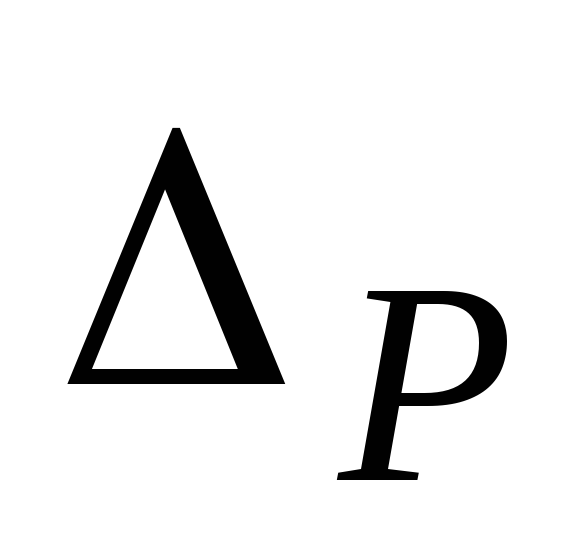і отримаємо силу:

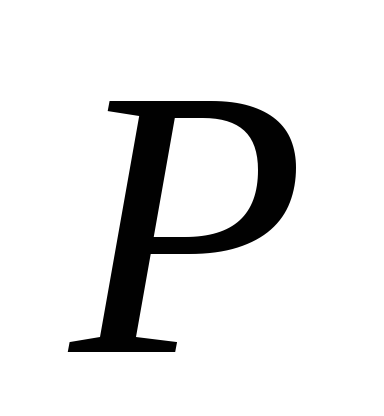Н.