При плоскому поперечному згинанні:

. (10.18)

Складаючи отримані значення для елементарної роботи внутрішніх сил і інтегруючи по довжині стержня, можна одержати повну роботу внутрішніх сил для загального випадку дії сил на стержень при виникненні всіх шести силових факторів:

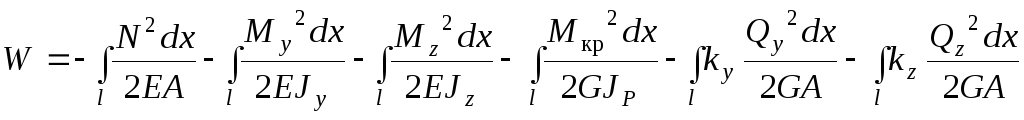. (10.19)

Потенціальна енергія при виникненні всіх шести внутрішніх силових факторів з урахуванням набуває вигляду:

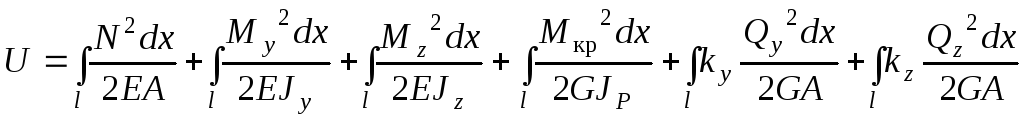. (10.20)

З наведеної формули видно, що потенціальна енергія деформації є квадратичною функцією узагальнених сил або узагальнених переміщень, оскільки останні лінійно зв'язані з узагальненими силами. Отже, потенціальна енергія деформації завжди додатна. Її величина не залежить від порядку навантаження і цілком визначається остаточними значеннями зусиль і переміщень. Відзначимо також, що потенціальна енергія як квадратична функція узагальнених навантажень не підкоряється принципові незалежності дії сил. Це означає, що потенціальна енергія, накопичена в результаті дії групи сил, не дорівнює сумі потенціальних енергій, викликаних дією кожного навантаження окремо. Принцип незалежності дії сил при обчисленні потенціальної енергії можна застосовувати лише в тих випадках, коли переміщення по напрямку однієї узагальненої сили, спричинене дією іншої сили, дорівнює нулю.

Наведений вираз для потенціальної енергії деформації (10.20) був отриманий для статичного прикладення навантажень при збереженні рівноваги протягом усього процесу навантаження. Варто сказати, що отримані формули зберігають силу і при будь-якому способі прикладення навантажень, аби значення сил і деформації були зв'язані лінійною залежністю і відносилися до того моменту, коли встановиться рівновага конструкції.

Розглянемо кілька прикладів визначення переміщень з застосуванням потенціальної енергії деформації.

Приклад 10.1. Визначити величину потенціальної енергії деформації в шарнірно-стержневій системі (Рис.10.5), навантаженій у вузлі В вертикальною силою кН. Стержні АВ і ВС мають однакові площі поперечного перерізусм² і виготовлені з одного матеріалу МПа. Знайти (у мм) вертикальне переміщення вузла В.

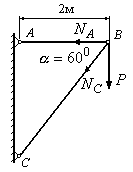
Рис.10.5

Розв’язок:

1. Знаходимо зусилля в стержнях АВ і ВС:

; (а)

. (б)

З рівняння (б) знаходимо: кН; з рівняння (а) знаходимо :кН.

2. Визначаємо потенціальну енергію системи:

Нм.

3. Знаходимо вертикальне переміщення вузла В. Знайдемо потенціальну енергію деформації через роботу, що дорівнює половині добутку сили , прикладеної у вузлі, на вертикальне переміщення вузла В:

.

Звідки: ммм.

Приклад 10.2. Обчислити потенціальну енергію деформацій балки на двох опорах (Рис.10.6), навантажену силою кН. Визначити переміщення під силою і посередині прольоту. Жорсткість поперечного перерізу балкикНм².

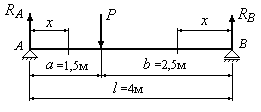
Рис.10.6

Розв’язок:

1. Обчислюємо опорні реакції: ;.

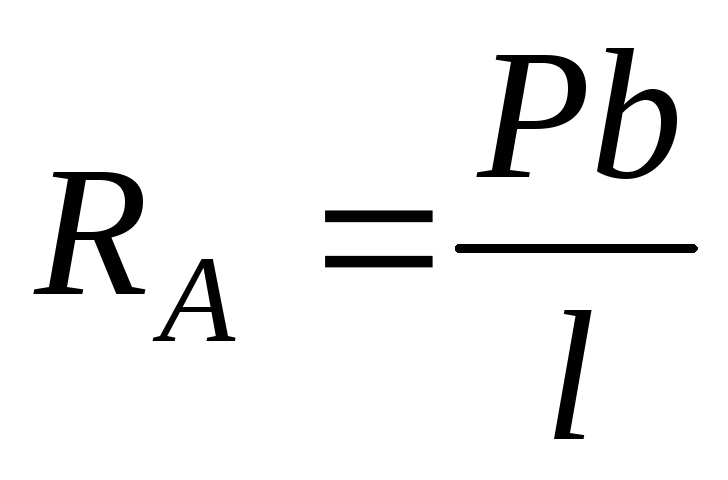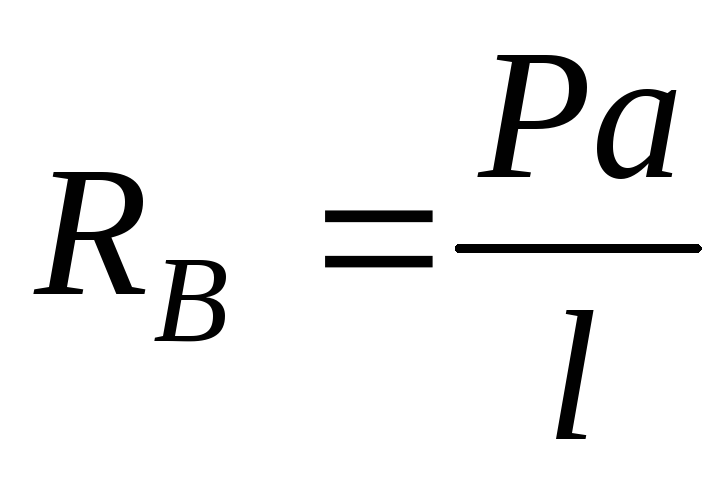2. Обчислюємо згинальний момент на кожній ділянці:

; .

3. Визначаємо потенціальну енергію деформації:

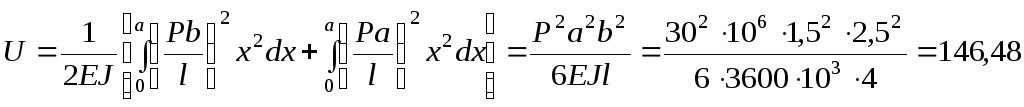Нм.

4. Знаходимо прогин під силою. Для цього обчислимо роботу сили на переміщенні балки:

; ,

звідки

м мм.

5. Знаходимо прогин посередині балки при . Одержимо:

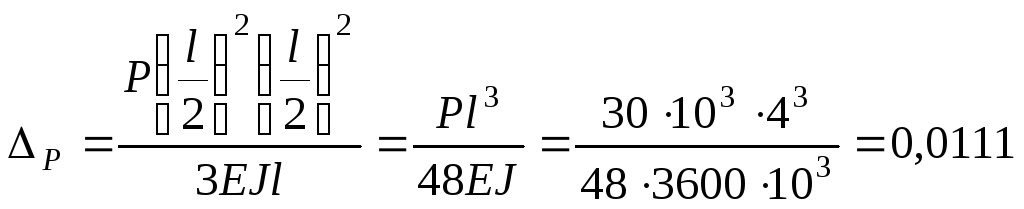ммм.

10.4. Визначення переміщень за методом Мора

Метод Мора є самим загальним методом визначенням переміщень у стержневих системах. У певному сенсі цей метод є універсальним, оскільки здатний визначати переміщення для різних видів деформації та у випадках складної деформації.

Розглянемо статично визначувану раму, навантажену в перерізі К зосередженого силою (Рис.10.7,а).

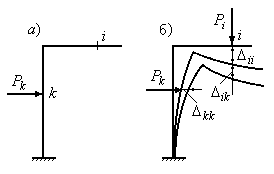
Рис.10.7

Потрібно визначити вертикальне переміщення перерізу , викликане зовнішньою силою, прикладеною в перерізі.

Зробимо так: спочатку прикладемо в перерізі фіктивну зосереджену силу. Рама деформується і перерізпереміститься на величину. Подвійна індексація у переміщення означає наступне: перший індекс означає найменування перерізу та напрямок, у якому прикладається фіктивна сила, тобто найменування того перерізу, у якому визначається переміщення. Другий індекс означає причину, що спричиняє це переміщення. У даному випадку – це сила. У більш загальному випадку це може бути будь-яке навантаження, прикладене до конструкції.

Потім прикладемо до рами діючу силу , після чого рама деформується ще більше. При цьому перерізпереміститься на величину, а переріз на величину . Переміщенняі є те саме переміщення, яке визначається.

Для його визначення будемо діяти таким чином. Обчислимо роботу, що виконують зовнішні сили при статичному навантаженні:

. (10.21)

В останньому члені рівняння (10.21) відсутній коефіцієнт , оскільки в момент прикладення до рами силифіктивна силабула незмінною за величиною і напрямком.

Обчислимо потенціальну енергію деформації з урахуванням того, що в рамі виникають поздовжня сила і згинальний момент, і їх дія відбувається одночасно (впливом поперечної сили будемо нехтувати):

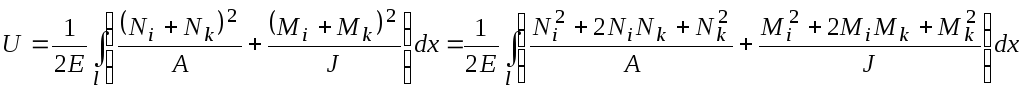
(10.22)

На підставі (10.3) робота зовнішніх сил (10.21) повинна дорівнювати накопиченій потенціальній енергії(10.22).

При складанні виразу для роботи зовнішніх сил ми використовували принцип незалежності дії сил (принцип суперпозиції). Але при обчисленні потенціальної енергії принцип суперпозиції в даному випадку не застосовуємо, оскільки потенціальна енергія є квадратичною функцією і накопичується вона в результаті одночасної дії сил і. У зв'язку з цим потенціальна енергія, що була накопичена в результаті дії групи сил, не дорівнює сумі потенціальних енергій, викликаних дією кожної сили окремо. Очевидно, у рівнянні (10.22) є члени, що не з'явилися б при підсумовуванні потенціальних енергій від дії кожної сили окремо. З'ясуємо, що це за члени і яким членам в рівнянні робіт (10.21) вони відповідають.

Для цього обчислимо величину потенціальної енергії деформації, що накопичується в рамі при дії кожної сили окремо:

При дії тільки сили :

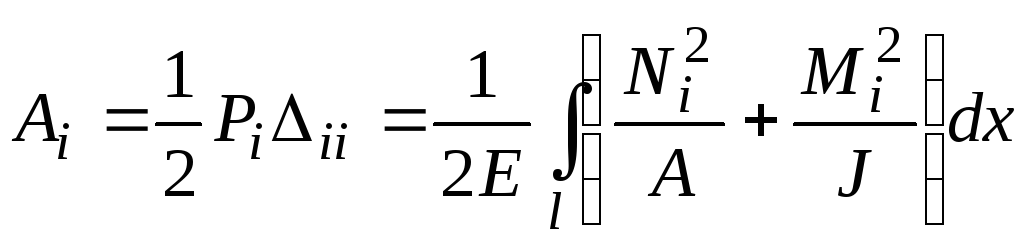. (10.23)

При дії тільки сили :

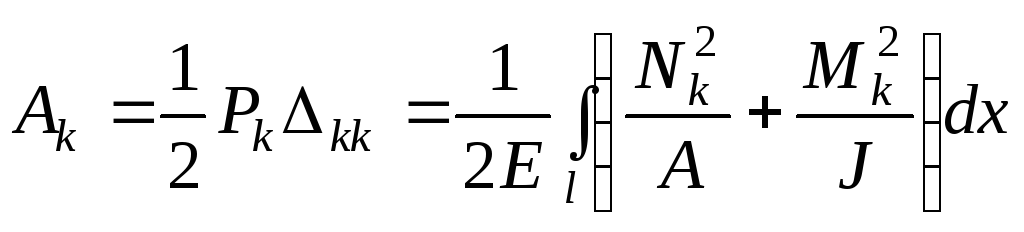. (10.24)

Перепишемо вираз (10.21) у вигляді:

(10.25)

і підставимо в це рівняння вирази (10.23) і (10.24). Одержимо:

.

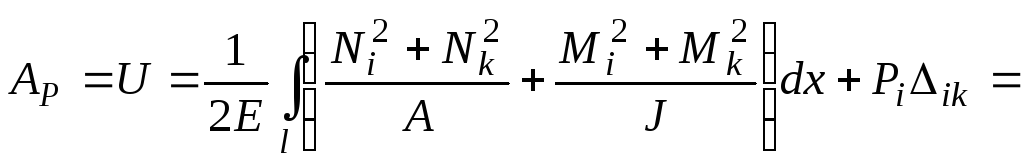
Після взаємних скорочень одержуємо:

. (10.26)

Покладемо . Тоді з виразу (10.26) знаходимо шукане переміщення:

. (10.27)

Вираз (10.27) і являє собою інтеграл Мора. Тут: і поздовжня сила і згинальний момент, що виникають у системі від дії зовнішньої сили .

Хрістіан Отто Мор (1835–1918) – відомий німецький вчений в галузі механіки. Був засновником графічної кінематики. Розробив метод розрахунку статично невизначуваних нерозрізних балок за допомогою рівняння трьох моментів. Дав узагальнення формулі Максвелла, створив теорію розрахунку статично невизначуваних систем методом сил.

Як уже відзначалося, метод Мора є методом універсальним. Для самого загального випадку навантаження, коли виникають усі шість внутрішніх силових факторів, інтеграл Мора набуває вигляду:

(10.28)

У більшості випадків при визначенні переміщень в балках і рамах можна нехтувати впливом поздовжньої деформації і деформації зсуву, з огляду лише на переміщення, що викликаються згинанням і крученням. Тоді формула (10.28) для плоскої системи набуває вигляду:

(10.29)

При просторовому навантаженні інтеграл Мора записується таким чином:

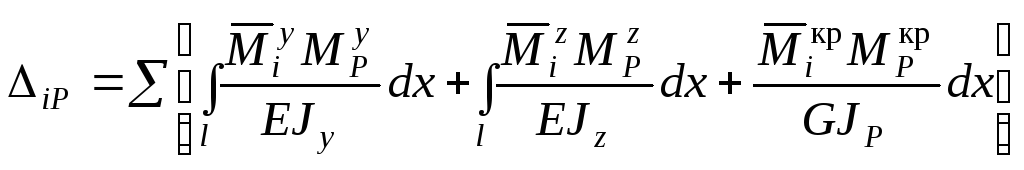(10.30)

При розрахунку шарнірних ферм, утворених прямими стержнями, у формулі Мора зберігається лише член, що містить поздовжню силу:

. (10.31)

Ця формула була отримана англійським вченим Джеймсом Клерком Максвеллом (1831–1879) і була узагальнена Мором.

Сформулюємо наступний порядок визначення переміщень за методом Мора:

1. Будують допоміжну систему, яку навантажують узагальненою одиничною силою в перерізі, де потрібно визначити переміщення. Визначаючи лінійні переміщення, у заданому напрямку прикладають одиничну силу, визначаючи кутові переміщення, прикладають одиничний момент.

2. Для кожної ділянки системи виписують вирази для силових факторів у довільному перерізі заданої (,,) і допоміжної (,,) систем.

3. Обчислюють інтеграли Мора (по ділянках у межах усієї системи). При розрахунку плоских рам і балок застосовують формулу (10.29), при розрахунку плоских ферм – формулу (10.31).

4. Якщо обчислене переміщення має додатний знак, то це означає, що його напрямок збігається з напрямком узагальненої одиничної сили. Від’ємний знак вказує на те, що дійсний напрямок шуканого переміщення протилежний напрямкові узагальненої одиничної сили.

Розглянемо приклади застосування методу Мора для визначення переміщень в стержневих системах.

Приклад 10.3. Використовуючи формулу Максвелла, знайти вертикальне переміщення вузла В (у мм) ферми, зображеної на рис.10.8,а, якщо жорсткість стержнів ферми однакова кН.

Розв’язок:

1. Визначаємо вантажні зусилля в стержнях ферми:

; (а)

. (б)

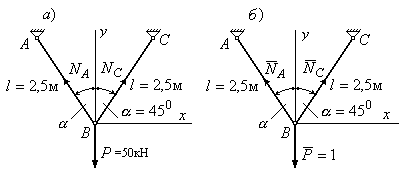
Рис.10.8

З рівняння (а) встановлюємо, що . З рівняння (б) знаходимо:

.

2. Зображуємо одиничний стан системи (Рис.10.8,б) і аналогічним чином знаходимо зусилля в стержнях ферми при одиничному стані:

.

3. Підставляємо отримані вирази для зусиль у вантажному та одиничному станах у формулу Максвелла (10.31) і перемножуємо. Одержуємо:

м = =50мм.

Приклад 10.4. Визначити за допомогою методу Мора прогин і кут повороту в перерізі В для балки, зображеної на рис.10.9,а, якщо жорсткість поперечного перерізу балки дорівнює кНм².

Розв’язок:

1. Зображуємо вантажний стан балки (Рис.10.9,а) і записуємо вираз для згинального моменту в перерізі :

. (в)

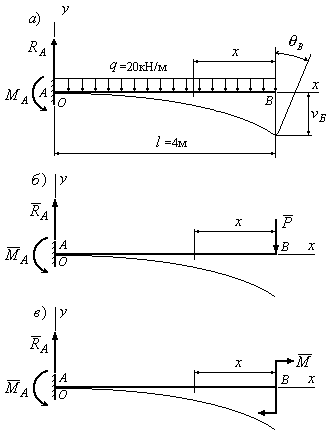
Рис.10.9

2. Зображуємо перший одиничний стан балки (Рис.10.9,б) і записуємо вираз для одиничного згинального моменту в перерізі :

. (г)

3. Підставляємо вираз (в) і (г) у формулу Мора (10.29) та обчислюємо інтеграл:

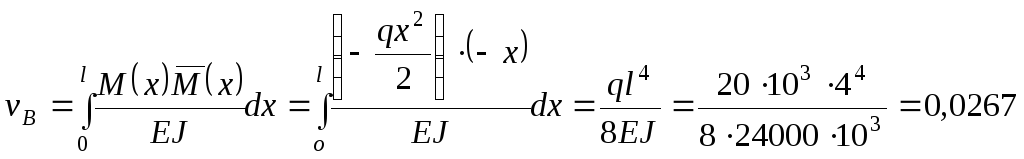м = 26,7мм.

4. Зображуємо другий одиничний стан (Рис.10.9,в), навантажуючи балку в перерізі В зосередженою одиничною парою сил і записуємо вираз для згинального моменту в перерізі :

. (д)

5. Підставляємо вираз (в) і (д) у формулу Мора (10.29) та обчислюємо інтеграл:

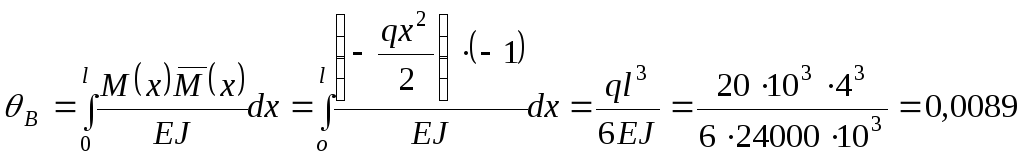рад.