Тема 10 загальні теореми про пружні системи. Загальні методи визначення переміщень

10.1. Закон збереження енергії. Узагальнена сила та узагальнена координата

Крім аналітичних методів обчислення прогинів і кутів повороту перерізів балок існують більш загальні методи, придатні для визначення переміщень у будь-яких пружних конструкціях. Ці методи засновані на двох основних принципах механіки: законі збереження енергії і початку можливих переміщень.

При статичному розтяганні або стисканні пружного стержня відбувається перетворення потенціальної енергії з одного виду в іншій. Як відомо, потенціальною називається такий вид енергії, яка накопичується в тілі при його пружних деформаціях. При навантаженні стержня зовнішніми силами частина потенціальної енергії вантажу, що діє на стержень, цілком переходить у потенціальну енергію деформації стержня. Дійсно, якщо ми будемо навантажувати стержень за допомогою малих вантажів (Рис.10.1), то при додаванні кожного такого вантажу підвішена вже частина навантаження буде опускатися і її потенціальна енергія буде зменшуватися, а потенціальна енергія деформації стержня відповідно збільшуватись.

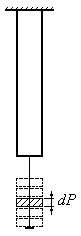
Рис.10.1

Це явище має місце при будь-якому виді деформації всякої пружної системи при статичному навантаженні. Таку систему можна розглядати як своєрідну машину, що перетворює один вид потенціальної енергії в інший.

Будемо називати “статичним” таке навантаження, що зростає поступово і таким чином, що прискореннями елементів конструкції можна нехтувати; передача тисків (сил) від однієї частини конструкції на іншу не змінює характеру руху цих частин, тобто швидкість залишається сталою і прискорення відсутнє.

При цих умовах деформація конструкції не буде супроводжуватися зміною кінетичної енергії системи, і буде мати місце лише перетворення потенціальної енергії з одного виду в іншій. При цьому ми нехтуємо магнітними, електричними і тепловими явищами, що супроводжують пружні статичні деформації тіла лише в дуже слабкій мірі.

Оскільки характер руху всіх елементів конструкції з часом не міняється, в кожний момент часу буде мати місце рівновага як для кожної частини конструкції в цілому під дією зовнішніх сил і реакцій, так і для кожного елемента цієї частини під дією зовнішніх сил і напружень, прикладених до цього елемента. Деформації конструкції, напруження в її частинах і реакції, що передаються від однієї частини до іншої, встигають змінюватися зі зростанням навантаження.

Таким чином, можна сказати, що повне перетворення одного виду потенціальної енергії в іншій має місце, якщо деформація відбувається без порушення рівноваги системи. Мірою енергії, що перетворилася на інший вид, є величина роботи, виконаної силами, які діють на конструкцію.

Позначимо величину накопиченої потенціальної енергії деформацій через , а зменшення потенціальної енергії зовнішніх навантажень через. Тоді величинавимірюється додатною роботою цих навантажень; з іншого боку, нагромадженню потенціальної енергії деформаціївідповідає від’ємна робота внутрішніх, міжчасткових сил , оскільки переміщення точок тіла при деформації відбуваються в зворотному стосовно внутрішніх сил напрямку.

Закон збереження енергії при деформаціях пружних систем набуває вигляду:

. (10.1)

Замінюючи в цій формулі величини ічисельно рівними їм значеннями робіті, одержуємо інше формулювання цього закону:

або . (10.2)

Це формулювання закону збереження енергії збігається є так званим “початком” або “принципом” можливих переміщень у застосуванні до пружних систем. Рівність (10.2) виражає ту думку, що при переміщеннях без порушення рівноваги сума робіт усіх сил, прикладених до точок тіла, дорівнює нулю.

Таким чином, принцип можливих переміщень у застосуванні до пружних систем є наслідком закону збереження енергії.

З формули (10.1) випливає, що потенціальна енергія деформації чисельно дорівнює роботі зовнішніх сил, виконаної ними при цій деформації:

(10.3)

Перш, ніж перейти до обчислення роботи зовнішніх сил, а через неї до потенціальної енергії деформації, розглянемо уявлення про узагальнену силу та узагальнену координату.

В задачах опору матеріалів і будівельної механіки зовнішнє навантаження відрізняється великою різноманітністю і зазвичай являє собою групи сил. Вираз для роботи групи постійних сил можна надати у виді добутку двох величин:

, (10.4)

у якому множник залежить тільки від сил групи і називаєтьсяузагальненою силою, а залежить від переміщень і називаєтьсяузагальненим переміщенням або узагальненою координатою.

Таким чином, під узагальненою силою варто розуміти будь-яке навантаження (зосереджені сили, зосереджені пари, розподілене навантаження), що викликає відповідне навантаженню переміщення. Узагальненою координатою будемо називати переміщення, що відповідає цій силі.

“Відповідність” полягає в тому, що мова йде про переміщення того перерізу, де прикладена розглянута сила, причому про таке переміщення, що добуток його на цю силу дає нам величину роботи; для зосередженої сили це буде лінійне переміщення в напрямку дії сили – прогин, подовження; для пари сил – це кут повороту перерізу в напрямку дії пари.

10.2. Робота зовнішніх сил. Теорема Клапейрона

Обчислимо роботу деякої узагальненої сили , прикладеної до будь-якої пружної лінійно деформівної системи (Рис.10.2,а). Припускається, що навантаження зростає від нуля до заданої величини досить повільно, щоб при цьому можна було знехтувати силами інерції мас, які переміщуються.

Припустимо, що у даний момент силі відповідає узагальнене переміщення. Нескінченно мале збільшення сили на величинувикликає нескінченно малий приріст переміщення. Елементарна робота зовнішньої сили, якщо знехтувати нескінченно малими другого порядку, дорівнює:

.

Повна робота, здійснена статично прикладеною узагальненою силою , на спричиненому цією самою силою узагальненому переміщенні, має вигляд:

. (10.5)

Інтеграл (10.5) становить площу діаграми для даної конструкції (Рис.10.2,б).

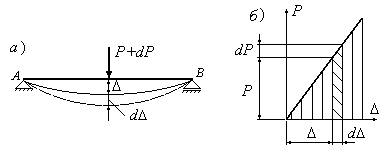
Рис.10.2

У лінійно деформівних системах переміщення пропорційні значенню сили (закон Гука):

, (10.6)

де  переміщення, спричинене силою .

Диференціюємо вираз (10.6):

.

Підставляючи цей вираз у формулу (10.5), матимемо:

.

З огляду на вираз (10.6), остаточно одержимо:

(10.7)

Отриманий вираз відомий як теорема Клапейрона: дійсна робота при статичній дії сили на пружну систему дорівнює половині добутку остаточного значення сили на остаточне значення відповідного узагальненого переміщення.

У разі статичної дії на пружну систему кількох узагальнених сил робота деформації дорівнює половині суми добутків остаточного значення кожної сили на остаточне значення відповідного сумарного переміщення і не залежить від порядку навантажування системи:

. (10.8)