
- •Тема 10 загальні теореми про пружні системи. Загальні методи визначення переміщень
- •10.1. Закон збереження енергії. Узагальнена сила та узагальнена координата
- •10.3. Обчислення потенціальної енергії деформації. Визначення переміщень при безпосередньому використанні потенціальної енергії
- •При плоскому поперечному згинанні:
- •10.5. Обчислення інтегралів Мора за способом Сімпсона
- •Таблиця 10.1
- •10.6. Матричний метод визначення переміщень за способом Мора-Сімпсона
- •10.7. Теореми про взаємність робіт та взаємність переміщень
- •10.8. Теорема Кастільяно. Теорема Лагранжа
- •10.9. Теорема про мінімум потенціальної енергії
- •10.10. Тести до теми №10 “Загальні теореми про пружні системи. Загальні методи визначення переміщень”
Таблиця 10.1
|
Значення
коефіцієнта
|
Вигляд
епюри
|
Вигляд
епюри
|
|
1 |
|
|
|
1/2 |
|
|
|
1/3 |
|
|
|
1/6 |
|
|
Формула
(10.37) одержала назву формули трикутників.
Тут
![]()
коефіцієнт, величина якого залежить
від вигляду епюр, що перемножуються
(Табл.10.1);
коефіцієнт, величина якого залежить
від вигляду епюр, що перемножуються
(Табл.10.1);
![]()
найбільший згинальний момент на
вантажний епюрі на ділянці;
найбільший згинальний момент на
вантажний епюрі на ділянці;
![]()
найбільший згинальний момент на одиничної
епюрі на ділянці;
найбільший згинальний момент на одиничної
епюрі на ділянці;
![]()
довжина ділянки.
довжина ділянки.
У таблиці
10.1 наводяться значення коефіцієнтів
![]() .
.
Метод Мора-Сімпсона називають методом перемножування епюр. Розглянемо порядок розв’язання задач методом Мора-Сімпсона.
1. Розбиваємо балку на ділянки і на кожній ділянці проставляємо по три “характерних” перерізи: на лівому кінці, посередині і на правому кінці ділянки.
2.
Обчислюємо значення вантажних моментів
у кожному з “характерних” перерізів
і будуємо епюру вантажних згинальних
моментів
![]() .
.
3. Зображуємо одиничний стан системи, прикладаючи в тому перерізі, де треба визначити переміщення, відповідну одиничну узагальнену силу: при визначенні прогину прикладають зосереджену одиничну силу; при визначенні кута повороту прикладають зосереджену одиничну пару.
4.
Обчислюємо значення одиничних моментів
в “характерних” перерізах і будуємо
епюру одиничних моментів
![]() .
Епюр одиничних моментів будуємо стільки,
скільки визначаємо переміщень.
.
Епюр одиничних моментів будуємо стільки,
скільки визначаємо переміщень.
5. Підставляємо обчислені значення вантажних і одиничних згинальних моментів у формулу Мора-Сімпсона й обчислюємо переміщення.
6. Знак переміщення буде додатним, якщо шукане переміщення збігається з напрямком відповідної узагальненої одиничної сили. Якщо напрямок переміщення і напрямок узагальненої одиничної сили не збігаються, знак переміщення буде від’ємним.
Розглянемо кілька прикладів визначення переміщень у стержневих системах за методом Мора-Сімпсона.
Приклад
10.5. Визначити методом
Мора-Сімпсона кут повороту перерізу В
балки, зображеної на рис.10.12,а, якщо
жорсткість поперечного перерізу балки
![]() кНм2.
кНм2.
Розв’язок:
1. Балка (Рис.10.12,а) має одна ділянку. Проставляємо “характерні” перерізи й обчислюємо в кожному з них вантажні моменти. Значення моментів в “характерних” перерізах проставлені на рис.10.12,б. Опорні реакції в даній задачі можна не визначати, згинальні моменти можна визначити, роблячи обчислення справа.
2.
Будуємо епюру вантажних згинальних
моментів
![]() .
.
3.
Зображуємо одиничний стан балки,
прикладаючи в перерізі В одиничний
момент
![]() (Рис.10.12,в). Знаходимо величини одиничних
згинальних моментів в “характерних”
перерізах. Значення цих моментів
проставлені на рис.10.12,г.
(Рис.10.12,в). Знаходимо величини одиничних
згинальних моментів в “характерних”
перерізах. Значення цих моментів
проставлені на рис.10.12,г.
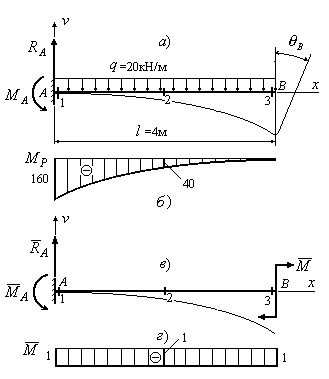
Рис.10.12
Будуємо епюру одиничних згинальних моментів (Рис.10.12,г).
5. Підставляючи знайдені значення вантажних і одиничних згинальних моментів у формулу (10.35), знаходимо кут повороту перерізу В:
![]() рад.
рад.
Приклад
10.6. Визначити вертикальне
і горизонтальне переміщення перерізу
В рами, зображеної на рис.10.13,а, якщо
жорсткість поперечного перерізу рами
![]() кНм2.
кНм2.
Розв’язок:
1. Розбиваємо раму на ділянки, розставляємо “характерні” перерізи і вибираємо точку спостереження (Рис.10.13,а).
2. Визначаємо вантажні згинальні моменти в “характерних” перерізах і будуємо епюру вантажних згинальних моментів (Рис.10.13,б).
3. Зображуємо перший одиничний стан (Рис.10.13,в), визначаємо згинальні моменти в “характерних” перерізах і будуємо епюру одиничних згинальних моментів (Рис.10.13,г).
4. Зображуємо другий одиничний стан (Рис.10.13,д), визначаємо згинальні моменти в “характерних” перерізах і будуємо епюру одиничних згинальних моментів (Рис.10.13,е).
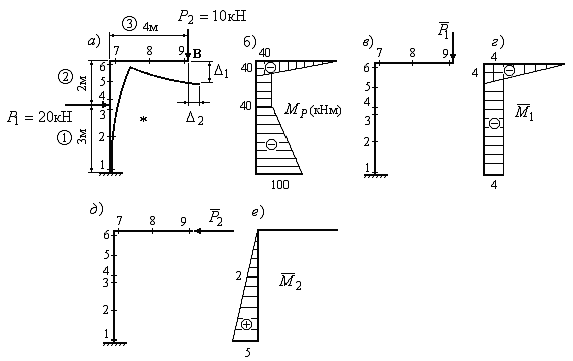
Рис.10.13
5.
Знаходимо вертикальне переміщення
вузла В, перемножуючи епюри згинальних
моментів
![]() і
і![]() .
Оскільки обидві епюри згинальних
моментів є лінійними, при перемножуванні
епюр скористаємося формулами трапецій
(10.36) і формулою трикутників (10.37). На
ділянці №1 будемо перемножувати епюри
за допомогою формули трапецій, на
ділянках №2 і №3 – за допомогою формули
трикутників:
.
Оскільки обидві епюри згинальних
моментів є лінійними, при перемножуванні
епюр скористаємося формулами трапецій
(10.36) і формулою трикутників (10.37). На
ділянці №1 будемо перемножувати епюри
за допомогою формули трапецій, на
ділянках №2 і №3 – за допомогою формули
трикутників:
![]()
![]() м
м
![]() мм.
мм.
Переміщення
вийшло додатним. Це означає, що напрямок
переміщення співпадає з напрямком
одиничної сили
![]() .
.
6.
Знаходимо горизонтальне переміщення
вузла В, перемножуючи епюри згинальних
моментів
![]() і
і![]() .
Так само, як і в попередньому пункті
будемо використовувати при перемножуванні
епюр формули трапецій і трикутників:
.
Так само, як і в попередньому пункті
будемо використовувати при перемножуванні
епюр формули трапецій і трикутників:
![]()
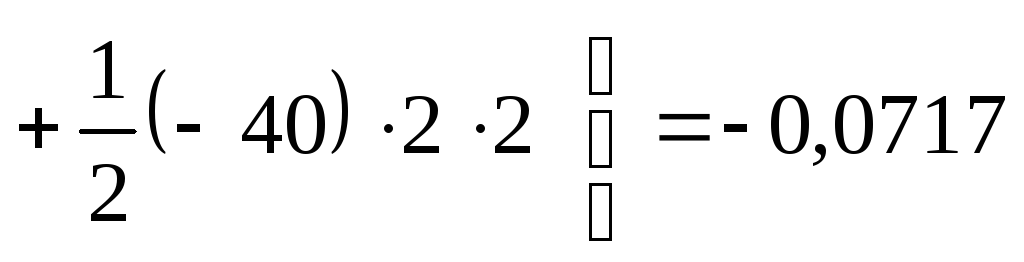 м
м
![]() мм.
мм.
Горизонтальне
переміщення
![]() виявилося від’ємним. Це означає, що
вузол В у горизонтальному напрямку
переміщується не ліворуч, куди була
спрямована одинична сила, а праворуч,
що відповідає фізичному змістові задачі.
виявилося від’ємним. Це означає, що
вузол В у горизонтальному напрямку
переміщується не ліворуч, куди була
спрямована одинична сила, а праворуч,
що відповідає фізичному змістові задачі.
