10.3. Обчислення потенціальної енергії деформації. Визначення переміщень при безпосередньому використанні потенціальної енергії

З виразу (10.3) випливає, що потенціальна енергія деформації чисельно дорівнює роботі зовнішніх сил на спричинених ними деформаціях і, отже, може бути обчислена з урахуванням теореми Клапейрона з виразу:

, (10.9)

де  узагальнена сила;  відповідна їй узагальнена координата.

Обчислимо потенціальну енергію для деяких видів деформації, використовуючи вираз (10.9).

При статичному розтяганні і стисканні стержня силами величина роботи, а, отже, і величина потенціальної енергіїдорівнює:

, (10.10)

де  поздовжня сила;  абсолютне подовження стержня;  модуль пружності першого роду;  площа поперечного перерізу стержня;  довжина стержня.

У разі зсуву:

, (10.11)

де  поперечна сила;  розмір поперечного перерізу;  величина абсолютного зсуву;  модуль пружності другого роду (модуль зсуву);  площа поперечного перерізу.

При крученні:

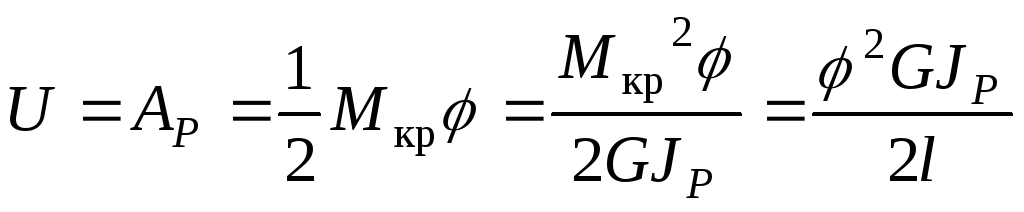, (10.12)

де  крутний момент;  кут закручування;  полярний момент інерції;  довжина стержня, що скручується.

При чистому згинанні кінцеві перерізи балки (Рис.10.3) під дією згинальних моментів повернуться на кут , де центральний кут осі балки, що зігнулася по дузі радіусом .

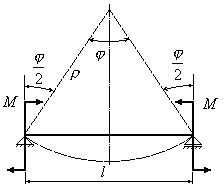
Рис.10.3

Тоді

. (10.13)

При плоскому поперечному згинанні роботу на спричинених зовнішніми силами переміщеннях виконує також і поперечна сила . Обчислимо цю роботу[3].

Як відзначалося раніше, поперечні сили є рівнодіючими розподілених у точках перерізу дотичних напружень (Рис.10.4,а). Останні в будь-якій елементарній площадці, паралельній нейтральної лінії перерізу (Рис.10.4,б), відповідно до формули Журавського є такими:

,

де  статичний момент площі відсіченої частини перерізу відносно нейтральної лінії .

На підставі закону Гука взаємний зсув двох розташованих на одній висоті площадок на торцяхі(Рис.10.4,в):

.

Отже, робота внутрішніх елементарних сил при їх зростанні від нуля до остаточного значення

Інтегруючи в межах перерізу , одержимо роботу поперчних сил:

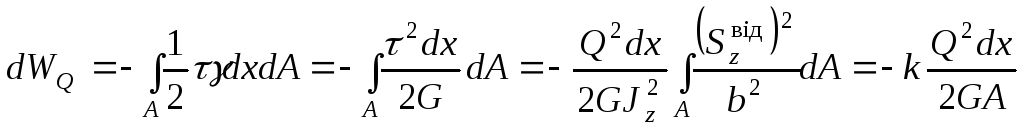, (10.14)

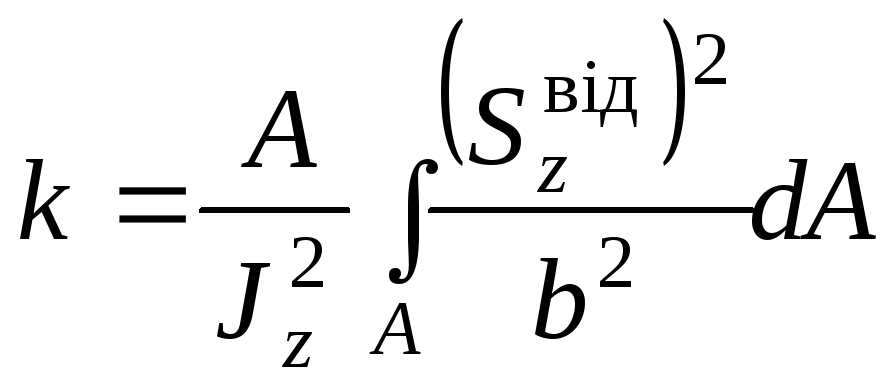
де  коефіцієнт, який залежить від форми поперечного перерізу;  жорсткість поперечного перерізу стержня при зсуві.

.

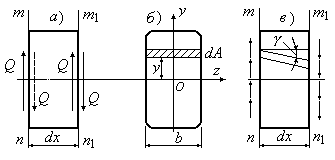
Рис.10.4

Для прямокутного перерізу ; для кругового ; для прокатних профілів приблизно, де площа стінки.

У випадку чистого зсуву дотичні напруження розподіляються рівномірно по перерізу:

.

Отже

. (10.15)

Отриманий вираз з точністю до знака збігається з виразом для потенціальної енергії при чистому зсуві (10.11).

Використовуючи чисельну рівність потенціальної енергії деформації абсолютній величині роботи внутрішніх сил, можна записати величину елементарної роботи при осьовому розтяганні і стисканні:

; (10.16)

при крученні:

. (10.17)