Щоб забезпечити запас стійкості для стиснутого стержня, потрібно, щоб стискальна сила , яка діє в стержні, не перевищувала допустимої величини:

, (13.1)

де  коефіцієнт запасу стійкості.

Отже, щоб виконати розрахунок стиснутого стержня на стійкість, потрібно вміти визначати для нього величину критичної сили.

13.2. Виведення формули Ейлера для визначення критичної сили стиснутого стержня

Задача визначення критичної сили для стиснутого стержня вперше була вирішена в 1744 році видатним математиком Леонардом Ейлером. Швейцарець за походженням, Леонард Ейлер значну частину свого життя прожив у Росії, був дійсним членом Петербурзької академії наук, написав близько 850 наукових праць, присвячених питанням астрономії, фізики, математики і механіки.

Метод Ейлера заснований на аналізі розгалуження можливих форм рівноваги пружної системи. Розглянемо його ідею більш докладно на прикладі центрально стиснутого, ідеально прямого стержня. При малих стискальних силах прямолінійна форма стержня є стійкою. При значних силах, що перевищують деяке критичне значення, вона є нестійкою, а стійкою буде криволінійна форма.

Таким чином, при теоретично можливе існування двох форм рівноваги.Найменше значення стискальної сили, при якому настає розгалуження форм пружної рівноваги, називається критичною силою. Отже, при критичній силі поряд з вихідною прямолінійною формою як би можлива суміжна, досить близька до неї викривлена форма.

Для виводення формули Ейлера розглянемо прямий стержень сталого перерізу, шарнірно обпертий на кінцях (Рис.13.2) [3]. Одна з опор стержня допускає можливість поздовжнього переміщення відповідного кінця стержня. Власною вагою стержня будемо нехтувати.

Навантажимо стержень центрально прикладеною поздовжньою стискальною силою і дамо йому досить незначне викривлення в площині найменшої жорсткості. Стержень утримується у викривленому стані. Це можливо, тому що.

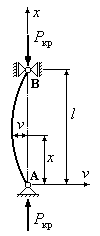
Рис.13.2

Деформація згинання стержня припускається досить малою, тому для розв’язання поставленої задачі скористаємося наближеним диференціальним рівнянням зігнутої осі стержня. Виберемо початок координат у точці А і напрямки осей координат, як показано на рис.13.2. Диференціальне рівнянням зігнутої осі стержня має вигляд:

. (13.2)

Обчислимо згинальний момент у перерізі , взятому на відстанівід початку координат:

. (13.3)

У формулі (13.3) знак “” взятий тому, що ордината є від’ємною. Якби стержень викривився опуклістю право, згинальний момент був би додатним при додатному прогині , а загальний результат від’ємним, тому що кривизна зігнутого стержня в обраній системі координат була б від’ємною. У цьому випадку перед додатним моментом проставляється знак “”.

Підставимо (13.3) у (13.2), одержимо:

. (13.4)

У формулі (13.4) взятий мінімальний момент інерції , тому що прогин відбудеться перпендикулярно осі найменшої жорсткості, якщо на кінцях стержня будуть кульові шарніри.

Поділяючи обидві частини рівняння (13.4) на мінімальну жорсткість і позначаючи дріб, приводимо рівняння (13.4) до вигляду:

. (13.5)

Загальний інтеграл цього рівняння має вигляд:

. (13.6)

Це рівняння укладає в собі три невідомих: А і В і значення , тому що величина критичної сили нам невідома.

Спочатку знайдемо сталі інтегрування А і В з граничних умов  умов поведінки стержня на опорах. Таких умов дві. Відповідно до першої умови на опорі А при прогин. Підставляючи ці значення поздовжньої координати і відповідне значення для прогину у рівняння (13.6), одержимо:

, звідки знаходимо .

Рівняння (13.6) набуває вигляду:

. (13.7)

Таким чином, стиснутий стержень викривляється за синусоїдою.

Для визначення другої сталої інтегрування А скористаємося другою граничною умовою: на опорі В при прогин.

Підставляючи значення поздовжньої координати і відповідне значення прогину у перерізі В у рівняння (13.7), маємо:

. (13.8)

З рівняння (13.8) випливає, що або стала , або нулю дорівнює.

Якщо коефіцієнт А дорівнюватиме нулю, то з рівняння (13.7) випливає, що прогин у будь-якому перерізі стержня дорівнює нулю, тобто стержень не буде викривлятися, залишаючись прямим. Це суперечить вихідним передумовам поведінки стержня. Отже, стала інтегрування . Нулю буде дорівнювати. Це можливо, коли аргумент функціїнабуває нескінченного ряду значень:

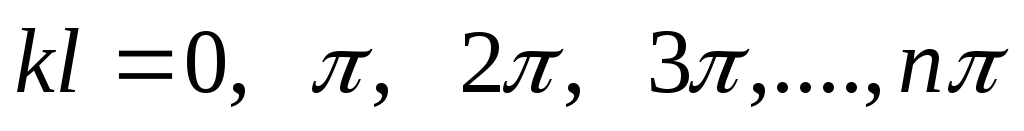, (13.9)

де  будь-яке ціле число.

Звідси . Зважаючи на те, що, величина критичної сили для стержня дорівнює:

. (13.10)

Таким чином, навантаження, здатне утримати злегка викривлений стержень у рівновазі, теоретично може мати цілий ряд значень. З практичної точки зору найбільш важливим є найменше значення осьової стискальної сили, при якій стає можливим поздовжнє згинання. Це значення стискальна сила буде мати при .

Якщо взяти перше значення кореня , то це буде означати, що критична силатакож буде дорівнювати нулю, а це суперечить умові задачі. Тому цей корінь відкидається і в якості найменшого значення приймається. Тоді критична сила набуває вигляду:

. (13.11)

Формула (13.11) називається формулою Ейлера для критичної сили стиснутого стержня з шарнірно обпертими кінцями. Значенню сили (13.11) відповідає згинання стержня за синусоїдою з однією напівхвилею (13.7):

. (13.12)

Значенням критичної сили вищих порядків відповідає викривлення за синусоїдами з двома, трьома і більше напівхвилями (Рис.13.3):

. (13.13)

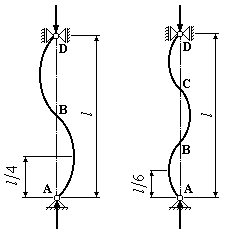
Рис.13.3

Таким чином, чим більше точок перегину буде мати синусоїдально викривлена вісь стержня, тим більшою має бути критична сила. Більш повні дослідження показують, що форми рівноваги, обумовлені формулами (13.8), нестійкі. Вони переходять у стійкі форми лише при наявності проміжних опор у точках В і С (Рис.13.3).

Величина сталої інтегрування залишилася невизначеною. Її фізичний зміст з'ясується, якщо визначимо максимальний прогин(стрілу прогину), скориставшись рівнянням (13.7). Максимальний прогинпри. Тоді.

Отже, загальний вигляд рівняння пружної лінії стиснутого стержня буде таким:

. (13.14)

Координату перерізу , у якому виникне максимальний прогин, знайдемо, узявши першу похідну від функції прогинупо поздовжній координатіі прирівнюючи її нулю:

, тобто або.

Найменше значення аргументу, при якому косинус дорівнює нулю, буде . Це означає, що:

, звідки . (13.15)

Якщо , то, а максимальний прогин виникне посередині стержня, що відповідає розглянутому випадкові закріплення опор стержня (Рис.13.2). Координати перерізів, у яких виникне максимальний прогин приі, відповідно дорівнюютьта(Рис.13.3). Як випливає з співвідношення (13.13) і рис.13.3, числоявляє собою число напівхвиль синусоїди, що розташовується на довжині зігнутого стержня.

13.3. Вплив способів закріплення кінців стержня на величину критичної сили

Формула Ейлера (13.11) для критичної сили виводилася для стержня з шарнірним закріпленням кінців. Цей випадок закріплення кінців стержня прийнято називати основним випадком. У цьому випадку на довжині стержня укладається одна напівхвиля синусоїди. З іншого боку, у практиці зустрічаються різні інші випадки обпирання кінців стержня. На рис.13.4 наведені деякі з них, які найбільш часто зустрічаються. Значення критичної сили для кожного з наведених випадків закріплення кінців можна вивести так само, як і формулу Ейлера для основного випадку, інтегруючи наближене диференціальне рівняння пружної лінії, але при інших граничних умовах. Однак на практиці застосовується більш простий спосіб визначення величини критичної сили, що використовує геометричну аналогію між поведінкою пружної лінії стиснутого стержня з шарнірним закріпленням кінців (основний випадок) і іншим способом обпирання кінців стержня. При використанні цього способу всі інші випадки закріплення кінців стержня зводяться до основного шляхом введення так званої зведеної або вільної довжини стержня.

Зведеною або вільною довжиною стержня називається умовна довжина шарнірно обпертого стержня, який має таку саму критичну силу, як і стержень з заданим закріпленням кінців. Судити про зведену довжину стержня можна по кількості напівхвиль, що укладаються на довжині стержня. З геометричної аналогії випливає, що в межах зведеної довжини стержень з довільним закріпленням кінців буде поводитися так само, як стержень з шарнірним обпиранням кінців. Уперше поняття зведеної або вільної довжини було введено професором Петербурзького інституту шляхів сполучення Ф.С.Ясинським.

Зведена довжина стержня обчислюється таким чином: , де довжина стержня з заданим обпиранням кінців;  коефіцієнт зведеної довжини.

З визначення зведеної довжини випливає, що коефіцієнт є деяким числом, на яке потрібно помножити довжину стержня з заданим закріпленням кінців, щоб одержати таку довжину умовного стержня, на якому розміститься одна напівхвиля синусоїди (13.7).

Рис.13.4

Для стержня, зображеного на рис.13.4,а довжина умовного стержня повинна бути в два рази більшою за задану довжину стержня. Верхня частина умовного стержня з шарнірним обпиранням кінців буде поводитися точно так само, як стержень з заданим закріпленням кінців. Коефіцієнт зведення довжини для цього випадку приймається . На рис.13.4,в одна напівхвиля поміщається на довжині, що складає 0,7 реальної довжини стержня. Коефіцієнт зведення довжини в цьому випадку складає. Для випадку жорсткого обпирання обох кінців стержня (Рис.13.4,г) довжина напівхвилі, заміряна між двома точками перегину, складає половину довжини стержня. Для цього випадку коефіцієнт. Для основного випадку (Рис.13.4,б) коефіцієнт, тому що на його довжині розміщається одна напівхвиля і, отже, зведена довжина стержнядорівнює реальній його довжині.

Для інших випадків закріплення кінців стержня значення коефіцієнтів зведення довжини стержня наведені в спеціальній довідковій літературі [4].