
- •Тема 15 задачі динаміки. Урахування сил інерції та ударної дії навантаження
- •15.1. Умови виникнення динамічних навантажень. Три задачі динаміки
- •15.2. Урахування сил інерції
- •15.2.1. Урахування сил інерції при поступальному русі
- •15.2.2. Урахування сил інерції при рівномірному обертанні
- •15.2.3. Урахування сил інерції при розрахунку на міцність стержня, що обертається навколо нерухомої осі
- •15.2.4. Урахування сил інерції при розрахунку дисків при їх обертанні
- •15.5. Виведення формули для коефіцієнта динамічності при ударі
- •15.6. Урахування власної ваги при ударі
- •15.7. Удар, що скручує, при екстреному гальмуванні
- •15.8. Тести до теми №15 “Задачі динаміки. Урахування сил інерції та ударної дії навантаження”
15.5. Виведення формули для коефіцієнта динамічності при ударі
Відразу ж відзначимо, що формула для коефіцієнта динамічності буде однаковою незалежно від виду деформації.
Розглянемо
балку, на яку з висоти
![]() падає вантаж
падає вантаж
![]() .
На балці в тому перерізі, у якому
відбувається удар, знаходиться вантаж
.
На балці в тому перерізі, у якому
відбувається удар, знаходиться вантаж
![]() (Рис.15.10).
(Рис.15.10).
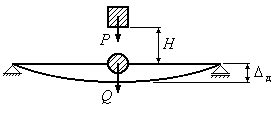
Рис.15.10
Відповідно
до прийнятої гіпотези удар будемо
вважати прилипаючим (абсолютно непружним).
У цьому випадку обидва вантажі об'єдналися
в один (![]() +
+![]() ), який, продовжуючи переміщатися униз,
згинає балку.
), який, продовжуючи переміщатися униз,
згинає балку.
П'ята
гіпотеза технічної теорії удару
стверджує, що вся кінетична енергія
удару
![]() переходить у потенціальну енергію
деформації
переходить у потенціальну енергію
деформації
![]() (
(![]() ).
).
Кінетичну енергію визначимо з виразу:
![]() .
(15.44)
.
(15.44)
Потенціальна енергія деформації, що накопичується в балці при дії динамічного навантаження, дорівнює:
![]() .
(15.45)
.
(15.45)
Коефіцієнт
![]() у формулі (15.45) береться тому, що сила
у формулі (15.45) береться тому, що сила
![]() змінюється від нуля до свого кінцевого
значення.
змінюється від нуля до свого кінцевого
значення.
Дорівнюючи значення кінетичної енергії (15.44) величині потенціальної енергії деформації (15.45), одержимо:
![]() .
(15.46)
.
(15.46)
Виражаючи
динамічне переміщення
![]() і підставляючи у формулу (15.46), маємо:
і підставляючи у формулу (15.46), маємо:
![]()
або після деяких перетворень:
![]() .
(15.47)
.
(15.47)
Рівняння (15.47) має два корені:
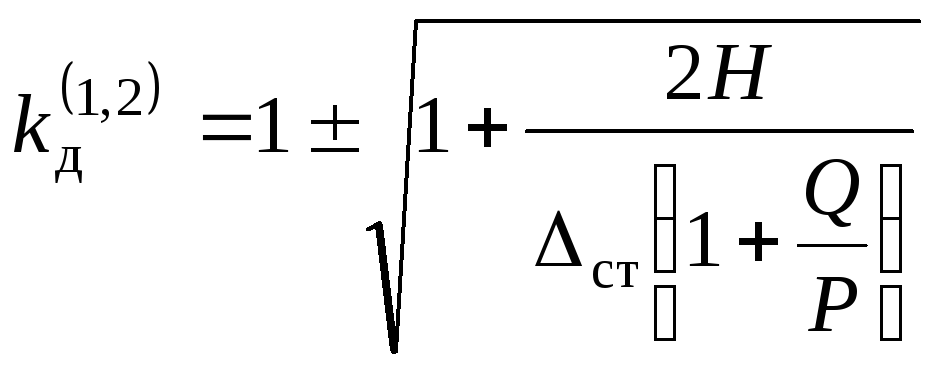 .
(15.48)
.
(15.48)
З двох коренів (15.48) залишаємо додатний:
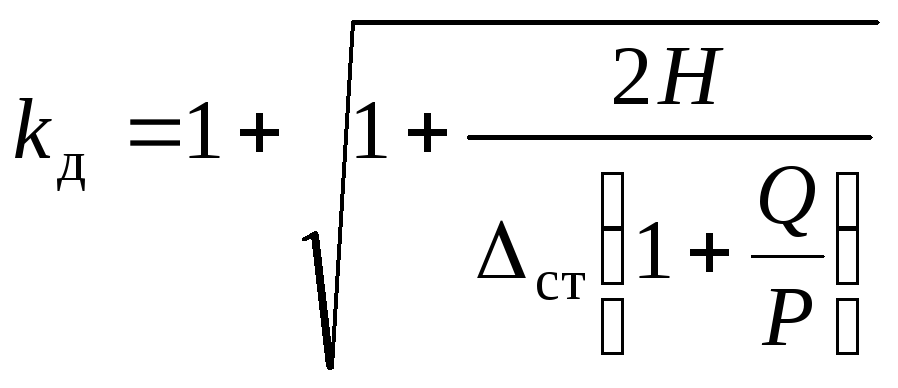 .
(15.49)
.
(15.49)
Таким чином, остаточно динамічний коефіцієнт при ударі набуває вигляду (15.49).
Отримане вирішення є наближеним, тому що при виводі формули (15.49) не був врахований цілий ряд факторів, а саме: удар вважався абсолютно непружним, у реальній системі він є частково пружним. Не були враховані місцеві деформації у точці, по якій наносився удар. Урахування місцевих деформацій може вплинути на остаточний результат. Через зроблені відступи від реальних умов формула (15.49) дає завищене значення динамічного коефіцієнта.
Якщо маса
на балці відсутня, тобто
![]() ,
а тіло
,
а тіло
![]() падає на невагому балку, то динамічний
коефіцієнт дорівнюватиме:
падає на невагому балку, то динамічний
коефіцієнт дорівнюватиме:
![]() .
(15.50)
.
(15.50)
З формули
(15.50) випливає, чим більше статичне
подовження
![]() ,
тим менший динамічний коефіцієнт. Чим
більша жорсткість системи, тим більша
величина ударної сили. Зменшити силу
удару можна, збільшивши
,
тим менший динамічний коефіцієнт. Чим
більша жорсткість системи, тим більша
величина ударної сили. Зменшити силу
удару можна, збільшивши
![]() .
При поздовжньому ударі, чим більша
довжина стержня і менша його жорсткість,
тим менший динамічний коефіцієнт, а
отже, менша динамічна сила і динамічні
напруження. Цим можна пояснити те, що
при буксируванні важких барж канати,
що з'єднують буксирний катер з баржею,
мають значну довжину. Короткі канати
при випадковому ударі, що виникає
внаслідок різних причин, не витримують
динамічного навантаження і розриваються.
.
При поздовжньому ударі, чим більша
довжина стержня і менша його жорсткість,
тим менший динамічний коефіцієнт, а
отже, менша динамічна сила і динамічні
напруження. Цим можна пояснити те, що
при буксируванні важких барж канати,
що з'єднують буксирний катер з баржею,
мають значну довжину. Короткі канати
при випадковому ударі, що виникає
внаслідок різних причин, не витримують
динамічного навантаження і розриваються.
Цим же пояснюється установка пружин і ресор, деформація яких сильно збільшує статичне переміщення, і в результаті зменшується динамічний коефіцієнт і динамічні напруження.
Величину
динамічного коефіцієнта при падінні
вантажу на невагому балку можна виразити
через швидкість падіння вантажу в момент
підльоту до балки. Для цього необхідно
замість величини
![]() підставити
величину
підставити
величину
![]() ,
тому що швидкість падіння вантажу в
момент, що передує ударові, пов'язана з
висотою падіння рівнянням
,
тому що швидкість падіння вантажу в
момент, що передує ударові, пов'язана з
висотою падіння рівнянням
![]() .
Отже:
.
Отже:
![]() .
(15.51)
.
(15.51)
Коли висота падіння дорівнює нулю, динамічний коефіцієнт дорівнює двом. Таке навантаження називається раптовим. Фізично цю задачу можна надати так: якщо на нитці підвісити вантаж, закріпивши його над балкою таким чином, щоб він торкався верху балки, але не тиснув на неї, а передавався цілком на нитку, і якщо при цьому нитку миттєво розсікти, то вантаж усією своєю величиною передасться на балку. Напруження і прогини в цьому випадку будуть у два рази більші, ніж при статичному навантаженні, при якому передбачається поступове наростання величини навантаження від нуля до кінцевого значення.
Якщо висота
падіння значно перевищує статичний
прогин
![]() ,
то одиницею у порівнянні з другим членом,
що стоїть під коренем, можна знехтувати.
Тоді:
,
то одиницею у порівнянні з другим членом,
що стоїть під коренем, можна знехтувати.
Тоді:
![]() .
(15.52)
.
(15.52)
