15.2.3. Урахування сил інерції при розрахунку на міцність стержня, що обертається навколо нерухомої осі

Розглянемо стержень довжиною , що обертається з постійною кутовою швидкістю навколо нерухомої осі (Рис.15.4,а). Відомі площа поперечного перерізу стержня , густина матеріалу . Потрібно визначити максимальну величину поздовжньої динамічної сили, що діє у стержні і величину максимальних нормальних напружень у стержні. Крім цього потрібно одержати закон зміни сил інерції уздовж стержня.

Помістимо початок координат на лівому кінці стержня у точці і виріжемо зі стержня на відстані від початку координат нескінченно малий елемент стержня довжиною . На вирізаний елемент будуть діяти нормальне прискорення , спрямоване убік початку координат і сила інерції (Рис.15.4,а).

Максимальну поздовжню силу в стержні, викликану дією сил інерції знайдемо з інтеграла:

. (15.10)

Максимальні нормальні напруження в стержні й умова міцності набувають вигляду:

. (15.11)

Рис.15.4

Так само, як і в ободі, міцність стержня від розміру площі не залежить, а залежить від квадрата колової швидкості на вільному кінці стержня .

Інтенсивність розподіленого навантаження уздовж стержня:

. (15.12)

Вираз (15.12) являє собою закон розподілу інтенсивності навантаження уздовж стержня. З нього видно, що інтенсивність розподілених сил інерції є лінійною функцією поздовжньої координати. Графік цієї залежності наведений на рис.15.4,б.

15.2.4. Урахування сил інерції при розрахунку дисків при їх обертанні

Зазвичай диск, що обертається, зазнає розтягання під дією відцентрових сил, що є для нього основним навантаженням, а також згинання. Зазвичай, сили інерції діють симетрично щодо осі диска, внаслідок чого напруження є функцією відстані від осі обертання.

Будемо вважати, що в тонкому плоскому диску сталої товщини , напруження за товщиною розподілені рівномірно, а напруження, паралельні осі диска, відсутні (). Таким чином, в диску виникає плоский напружений стан.

Розглянемо диск, що обертається зі сталою кутовою швидкістю [4]. Питома вага матеріалу диску . Сили інерції, що діють на виділену частину диску, виразимо у вигляді рівнодіючої (Рис.15.5), що лежить у серединній площині елемента:

.

Рис.15.5

Спроектуємо всі сили, що діють на виділений елемент, на вісь і прирівняємо нулю. Після деяких скорочень і перетворень, одержимо рівняння рівноваги у вигляді:

. (15.13)

Геометричні і фізичні рівняння при розрахунку обертових дисків будуть такими самими, як і в задачі Ламе (13.18)(13.21). Тому диференціальне рівняння (15.13) у переміщеннях з урахуванням (13.20), (13.21) має вигляд:

. (15.14)

Переписавши (15.14) у вигляді

і інтегруючи його послідовно двічі, знайдемо:

. (15.15)

Підставивши (15.15) у (13.20)(13.21), одержимо:

; (15.16)

, (15.17)

де

; .

Сталі і визначаються з граничних умов. Для диска з центральним отвором маємо наступні умови на внутрішньому () і зовнішньому ( ) контурах:

;

.

Відповідно до (15.16) ці умови дають два рівняння:

;

.

Вирішуючи сумісно цю систему рівнянь, знаходимо:

; (15.18)

. (15.19)

У випадку, коли і ,

; (15.20)

. (15.21)

Підставляючи останні значення та у формули (15.16) і (15.17), одержимо:

; (15.22)

. (15.23)

Введемо позначення:

; ; ; . (15.24)

Перепишемо з урахуванням введених позначень рівняння (15.22) і (15.23) для радіальних і колових напружень у вигляді:

; (15.25)

. (15.26)

Напруження додатне і досягає найбільшої величини при :

. (15.27)

Напруження теж додатне при всіх значеннях і досягає максимуму при :

. (15.28)

Порівнюючи (15.27) і (15.28), приходимо до висновку, що завжди має місце нерівність . Тому, використовуючи третю теорію міцності, умову міцності запишемо у вигляді:

. (15.29)

Формули для напружень у суцільному диску ( ) на підставі (15.16) і (15.17) набувають вигляду:

; (15.30)

. (15.31)

Якщо зовнішнє навантаження на зовнішньому контурі ( ) відсутнє, тобто , то згідно з (15.30) знаходимо:

. (15.32)

Підставляючи (15.32) у (15.30) і (15.31), одержимо:

; (15.33)

. (15.34)

Обидва напруження додатні і зростають з наближенням до центра. У центрі диска при

. (15.35)

Відповідно до (13.19) радіальне переміщення

. (15.36)

Зважаючи на те, що

,

радіальне переміщення дорівнює

. (15.37)

Для визначення переміщення на зовнішньому контурі диска у формулу (15.37) необхідно підставити значення ; ; .

15.3. Приклади розрахунку елементів конструкцій з урахуванням впливу сил інерції

Приклад 15.1. Вантаж вагою 30кН піднімається рівноприскорено за допомогою сталевого троса, причому за перші дві секунди він піднімається на висоту м. Площа поперечного перерізу троса см², довжина троса м, питома вага матеріалу кН/м³. Визначити найбільше нормальне напруження в тросі без урахування і з урахуванням його власної ваги.

Розв’язок:

1. Скориставшись формулою для для рівноприскореного руху , знайдемо величину прискорення руху вантажу:

м/с².

2. Знаходимо динамічний коефіцієнт при поступальному русі:

.

4. Визначаємо динамічне напруження в тросі без урахуванням його ваги:

МПа.

5. Визначаємо динамічне напруження в тросі з урахуванням його власної ваги:

МПа.

Приклад 15.2. На двох балках коритного профілю №20 встановлено лебідку вагою кН, що піднімає вантаж кН за допомогою сталевого троса (Рис.15.6,а). Підйом вантажу відбувається із сталим прискоренням м/с². З огляду на вагу вантажу, лебідки і власну вагу балок, визначити величину найбільшого нормального напруження в балках і тросі.

Рис.15.6

Розв’язок:

1. Визначаємо коефіцієнт динамічності:

.

2. Визначаємо динамічне зусилля в тросі:

кН.

3. Обчислюємо динамічне напруження в тросі:

МПа.

4. Розрахункова схема наведена на рис.15.6,б. Максимальний згинальний момент у балках від ваги лебідки , динамічного зусилля в тросі і власної ваги балок:

кНм,

де кН/м – вага одного метра швелера №20.

4. Визначаємо максимальне нормальне напруження в балках:

МПа.

Приклад 15.3. Чавунний стержень круглого поперечного перерізу, що несе на вільному кінці вантаж (Рис.15.7), обертається навколо горизонтальної осі з постійною кутовою швидкістю с^1. Визначити величину вантажу , при якому відбудеться руйнування стержня, якщо границя міцності чавуну при розтяганні дорівнює МПа, питома вага кН/м³.

Рис.15.7

Розв’язок:

1. Обчислимо сумарну інерційну силу, викликану обертанням вантажу і стержня:

.

2. Повне динамічне зусилля в стержні:

.

3. Умова руйнування стержня має вигляд:

.

4. Руйнівна сила дорівнює:

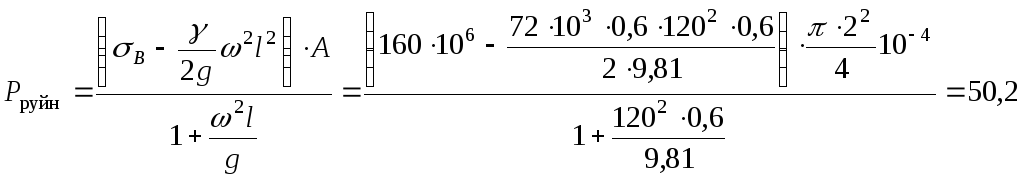Н.

Приклад 15.4. Найбільша безпечна колова швидкість для чавунних маховиків приймається м/с. Нехтуючи впливом спиць і вважаючи питому вагу чавуну кН/м³, визначити найбільше розтягальне напруження в ободі маховика при зазначеній коловій швидкості.

Розв’язок:

Найбільше розтягальне напруження в ободі маховика визначимо, скориставщись формулою:

МПа.

Приклад 15.5. Швидкість обертання чавунного маховика за секунди рівномірно змінюється з об/хв до об/хв. Обід маховика важить кН, радіус інерції його дорівнює см. Визначити величину крутного моменту і найбільше дотичне напруження, що виникає внаслідок цієї зміни швидкості вала, на який насаджений маховик, якщо діаметр вала дорівнює мм.

Розв’язок:

1. Визначаємо величину прискорення обертання вала:

с ^1.

2. Визначаємо величину крутного моменту, що виникає внаслідок зміни швидкості вала:

кНм.

3. Визначаємо максимальне дотичне напруження, що виникає у валу:

МПа.

Приклад 15.6. На вал діаметром мм насаджений маховик з моментом інерції Нмс². Швидкість обертання вала дорівнює об/хв. Раптово починає діяти гальмо, що зупиняє маховик через обертів. Вал з маховиком відключаються від двигуна до початку гальмування. Визначити величину найбільшого дотичного напруження у валі. Тертям у підшипниках знехтувати.

Розв’язок:

1. Визначаємо прискорення, що виникло в результаті гальмування:

1/хв².

2. Визначаємо час до зупинки:

об.

Звідки:

хв = 6 с.

3. Визначаємо величину крутного моменту:

кНм.

4. Обчислюємо максимальне дотичне напруження у валі:

МПа.

Приклад 15.7. Шкіряний ремінь шириною см і товщиною мм перекинутий через шків діаметром м і передає потужність к.с. Шків обертається з постійною швидкістю і робить об/хв. Вага 1см³ ременя дорівнює 10Н ( кН/м³). Визначити напруження у ремені без урахування і з урахуванням виникаючих у ньому сил інерції, якщо відношення зусиль у гілках ременя дорівнює .

Розв’язок:

1. Визначаємо величину зовнішнього моменту, що передає вал при обертанні:

кНм.

2. Крутний момент, що діє у валу, дорівнює за величиною зовнішньому і складається з моментів, що створюють зусилля в ремені:

кНм,

Звідки

кН.

Натяг у тій гілці ременя, що набігає, без урахування сил інерції буде в 2,5 рази більший: кН.

3. Напруження у гілці ременя, що набігає, без урахування впливу сил інерції знайдемо, розділивши зусилля в ній на площу поперечного перерізу:

МПа.

4. При урахуванні сил інерції, що виникають у ремені, зусилля у гілках збільшаться на величину:

.

Додаткові напруження від впливу сил інерції складають:

МПа.

Сумарні напруження у ремені дорівнюватимуть:

МПа.

Приклад 15.8. Вантаж вагою Н обертається з постійною кутовою швидкістю с^–1 у горизонтальній площині, утримуваний сталевою пружиною, що має до деформації довжину см (Рис.15.8). Знайти подовження пружини і найбільше дотичне напруження в ній, якщо вона має витків при середньому радіусі витка см і радіусі дроту мм. Тертям вантажу об горизонтальну площину знехтувати.

Рис.15.8

Розв’язок:

1. Визначаємо динамічну силу, що виникає в пружині при обертанні:

, (а)

де  маса вантажу;  подовження пружини, викликане силою інерції;  модуль зсуву.

З рівняння (а) динамічна сила дорівнює:

Н.

2. Обчислюємо подовження пружини :

м.

3. Визначаємо максимальне дотичне напруження, що виникає у пружині:

МПа.

Приклад 15.9. Вал і жорстко зв'язаний з ним ламаний стержень того ж поперечного перерізу обертаються з постійною кутовою швидкістю навколо осі АВ (Рис.15.9). Діаметр вала мм. Визначити допустиме число обертів вала за хвилину при допустимому напруженні МПа і питомою вагою матеріалу . Довжина ділянки ламаного стержня м.

Рис.15.9

Розв’язок:

1. Складемо розрахункову схему (Рис.15.9,б). Для цього прикладемо до елемента DK розподілене навантаження інтенсивності , викликане обертанням вала навколо осі , а також рівнодіючу сил інерції , що виникає у вертикальному стержні CD. Для зручності розрахунків виразимо рівнодіючу сил інерції через інтенсивність розподіленого навантаження .

2. Знайдемо опорні реакції в перерізах А і В. Для цього складемо два рівняння рівноваги у загальному виді:

;

.

Вирішуючи ці рівняння щодо опорних реакцій, знаходимо:

; .

3. Розбиваємо раму, зображену на рис.15.9,б, на ділянки, вибираємо точку спостереження, проставляємо на кожній ділянці “характерні” перерізи, обчислюємо в цих перерізах у загальному виді згинальні моменти і будуємо епюру згинальних моментів (Рис.15.9,в).

4. Визначаємо розрахункове значення згинального моменту. Розрахунковим є максимальний згинальний момент, що діє в перерізі С:

.

5. Обчислюємо в загальному виді максимальне нормальне напруження у валу, викликане силами інерції, і записуємо умову міцності:

.

6. З умови міцності визначаємо допустиму кутову швидкість обертання вала:

с ^–1.

Або

об/хв.

Приклад 15.10. Суцільний сталевий диск сталої товщини обертається з постійною кутовою швидкістю с^–1 навколо центральної осі, перпендикулярної до його серединної площини. Визначити найбільше нормальне напруження в диску, якщо його діаметр м.

Розв’язок:

Для суцільного диску радіальні й колові напруження визначаються за допомогою виразів (15.33) і (15.34):

;

.

Максимальне напруження виникає у центрі диска при і визначається за допомогою формули (15.35):

МПа.

Приклад 15.11. Сталевий диск сталої товщини, діаметром см має центральний отвір діаметром см і рівномірно обертається навколо центральної осі, перпендикулярної до його серединної площини. Визначити найбільшу допустиму кількість обертів диска, при якій максимальне нормальне напруження в ньому не перевищить МПа.

Розв’язок:

1. Для дисків з отвором запишемо умову міцності за третьою теорією (15.29):

(а)

і визначимо значення коефіцієнтів і , що входять у це рівняння:

; (б)

; . (в)

2. Підставимо (б), (в) у (а), звідки знайдемо величину максимально допустимої кутової швидкості:

с ^–1

або

об/хв.

15.4. Розрахунок на міцність при ударних навантаженнях. Технічна теорія удару

Під ударом варто розуміти взаємодію тіл, що рухаються, в результаті їх зіткнення, зв'язане з різкою зміною швидкостей точок цих тіл за досить малий проміжок часу. Час удару вимірюється в тисячних, а іноді в мільйонних частках секунди, а сила удару досягає значної величини, наприклад, удар падаючого вантажу при забиванні паль, дія ковальського молота на шматок металу при куванні та ін. При розрахунку конструкцій, що зазнають удару, доводиться мати справу не з прискореннями, а з імпульсом сили удару. Тому принцип Д'Аламбера (кінетостатики) при ударі не працює.

У фізиці розрізняють дві фази удару. У першій фазі центри ваги тіл, що зазнають удару, зближуються, а сила взаємодії між тілами зростає, досягаючи максимального значення в момент найбільшого зближення тіл, коли швидкість відносного руху зменшується до нуля.

У другій фазі (фазі відновлення) центри ваги тіл віддаляються один від одного, сили взаємодії зменшуються до нуля наприкінці удару, коли припиняється контакт тіл, або обертаються в сталу величину, якщо удар не є абсолютно пружним. Відбувається швидкий обмін енергіями між тілом, що вдаряє, та тілом, яке зазнає удару. Такий удар вважається відскакуючим. Урахування такого удару пов'язане з вивченням місцевих деформацій у місці контакту (так звана контактна задача теорії пружності), а також з вивченням явища хвильового поширення деформації в пружному тілі. Задача виявляється складною, тому при інженерних розрахунках використовується наближена технічна теорія удару, заснована на наступних гіпотезах:

1. Удар є прилипаючим на відміну від пружного удару, який розглядається у фізиці. При ударі, що прилипає, обидва тіла починають рухатися спільно.

2. Напруження в стержні не перевищують границі пропорційності, виконується закон Гука, модуль пружності залишається таким самим, як і при статичному навантаженні.

3. Деформації розповсюджуються по тілу миттєво.

4. Деформовані стани тіл при статичному і динамічному навантаженнях подібні.

5. Уся кінетична енергія удару переходить у потенціальну енергію пружної деформації .

15.5. Узагальнення динамічного коефіцієнта

Розглянемо докладніше гіпотезу технічної теорії удару №4. Гіпотеза стверджує наявність подібності між деформованими станами при статичному і динамічному навантаженнях. Ця подібність між динамічними і статичними зусиллями, напруженнями та , деформаціями та може бути виражена за допомогою коефіцієнта динамічності у вигляді:

. (15.38)

Встановимо зв'язок між потенціальною енергією деформації, що накопичується в тілі при ударі, і потенціальною енергією при статичному навантаженні.

Загальний вираз для потенціальної енергії деформації при статичному навантаженні має вигляд:

. (15.39)

Аналогічний вид набуває загальний вираз для потенціальної енергія при динамічному навантаженні:

, (15.40)

де:  будь-яке внутрішнє зусилля (, , та ін.);  жорсткість поперечного перерізу при будь-якому виді деформації ( , , та ін).

Виразимо динамічне зусилля через статичне з (15.38) і підставимо в (15.40). Одержимо:

. (15.41)

Доповнимо ряд співвідношень (15.38) отриманим співвідношенням між динамічною і статичною потенціальними енергіями:

. (15.42)

Аналізуючи останній вираз, дістаємо висновку, що, знаючи коефіцієнт динамічності і статичні зусилля, напруження, переміщення, потенціальну енергію та ін., можна знайти динамічні значення зусиль, напружень, переміщень і потенціальної енергії. Зокрема, умову міцності при ударі можна записати у вигляді:

. (15.43)