- •Chapter 14. Gas turbine engine starting systems
- •14.1. General information
- •14.1.1. Starting system designation
- •14.1.2. Requirements to the starting system
- •14.2. Structure of gas turbine engine starting systems
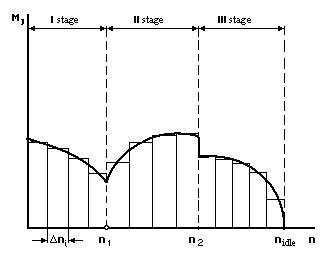
- •14.3. Gas turbine engine starting diagram. Characteristic of start stages
- •Table 14.1 Typical rotational speeds of gte rotor
- •14.4. Calculation of gas turbine engine starting system
- •14.4.1. Determination of necessary maximum power of the starter
- •14.4.2. Starting diagram calculation
- •Fig. 14.5. Starter power dependence versus rotor rotational speed, for constant torque
- •Using equation (14.1), we will get
- •From equation (14.1) and in view of formula (14.6) we will get:
- •For the tpEs a rotor dynamical moment of inertia equals:
- •Fig. 14.8. Diagram of the redundant torque
- •14.5. Types of aeroengine starters
- •14.5.1. Electrical starters
- •14.5.2. Turbine starters
- •Fig. 14.17. Schematic of an air turbine starter
- •Fig.14.19. Schematic of the gas turbine starters:
- •Fig. 14.21. Cartridge-pneumatic starter scheme
- •14.5.3. Hydraulic starters
- •Questions for self-check
From equation (14.1) and in view of formula (14.6) we will get:
![]() (14.8)
(14.8)
Equating the right members of ratios (14.7) and (14.8), we will get the formula for calculation of a constant С:
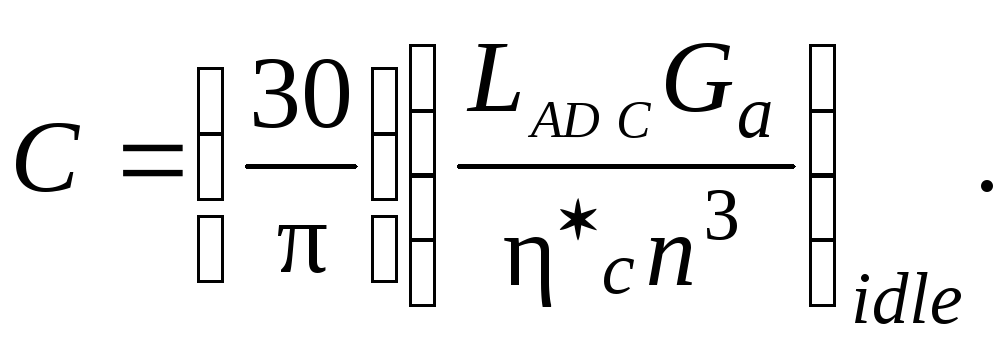
All values of this formula given in brackets should correspond to an idle. They are determined with the help of the engine throttling characteristics. For an approximate estimation of C constant, specified values, which would correspond to a design rating, can be used.
With C known, antitorque moment is calculated by the formula
MR = (1,05...1,07)С n2. (14.9)
The numeric values of expression (13.9) given in brackets can be augmented up to values 1,25...1,30 for the TPEs, prop-fan engines and multishaft TFEs with large by-pass ratio. This method is correct because in these types of a turbine engine a transfer of a considerable part of energy from a starter device to a propeller or in the secondary flow takes place.
The reliable data for determination of the turbine torque МТ (n) can be got only on the basis of bench tests of the turbine unit or engine as a whole. In approximate calculations this function is approximated by segments of two straight lines, which pass through known points on a MR (n) curve (Fig. 14.7). The turbine torque for the second stage of start МТ II is determined with the help of a straight line segment. It is drawn through points 1 and 2. A straight line segment for the torque МТ III (third stage of starting) is drawn through points 2 and 3. The position of the point 2 is in the middle of the third stage. The position of the point 3 corresponds to condition of МТ =MR at an idling.
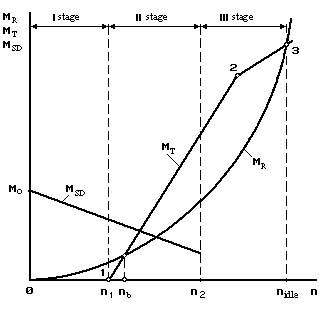
Fig. 14.7. Linear approximating of the turbine torque characteristics
The starting duration is calculated on the basis of a dynamic equation of unsteady rotated motion of a rotor (second Newton’s law for rotation of a body with acceleration), pursuant to which the moment of inertia forces of a rotated rotor Мj, is equal to product of its mass polar moment of inertia JP and an angular acceleration:
![]() (14.10)
(14.10)
Using another formula of equation (14.10)
![]()
we have
![]() (14.11)
(14.11)
For the TJEs and TFEs rotor mass polar moment of inertia JPequals, [kgm2]:
![]() ,
,
where
J0
is a rotor dynamical moment of inertia; Jc
and Jt
are the compressor and turbine rotor mass polar moment of inertia; kc
and
kt
are the statistical coefficients (![]() =3,5…5,5;
=3,5…5,5;![]() =9,5…10,5);ic
and it
are the compressor and turbine stages quantities; Dc max
and Dt max
are the maximum compressor and turbine rotor diameters.
=9,5…10,5);ic
and it
are the compressor and turbine stages quantities; Dc max
and Dt max
are the maximum compressor and turbine rotor diameters.
For the tpEs a rotor dynamical moment of inertia equals:
![]() ,
,
where
for single row propeller
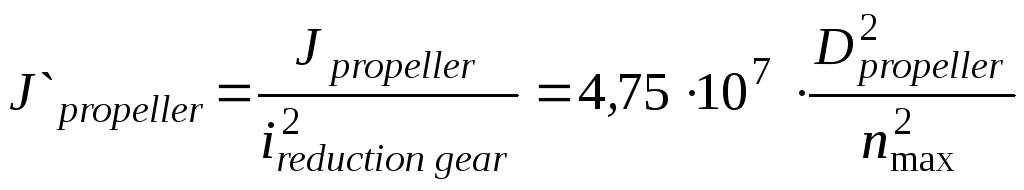 ,[kgm2];
Jpropeller
is
a propeller moment of inertia;
ireduction
gear
is a reduction gear ratio; Dpropeller
is a propeller diameter; nmax
is a maximum rotor rotational speed; and for double-row propeller
,[kgm2];
Jpropeller
is
a propeller moment of inertia;
ireduction
gear
is a reduction gear ratio; Dpropeller
is a propeller diameter; nmax
is a maximum rotor rotational speed; and for double-row propeller
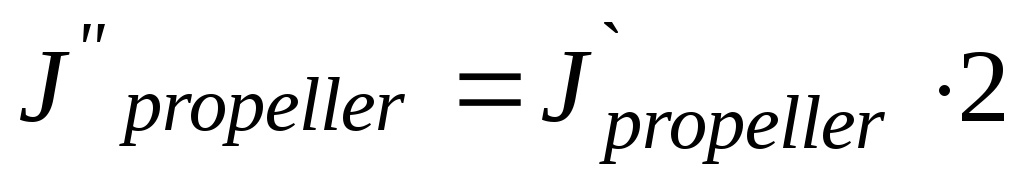 .
.
Starting duration is discovered by integration of a ratio (14.11)
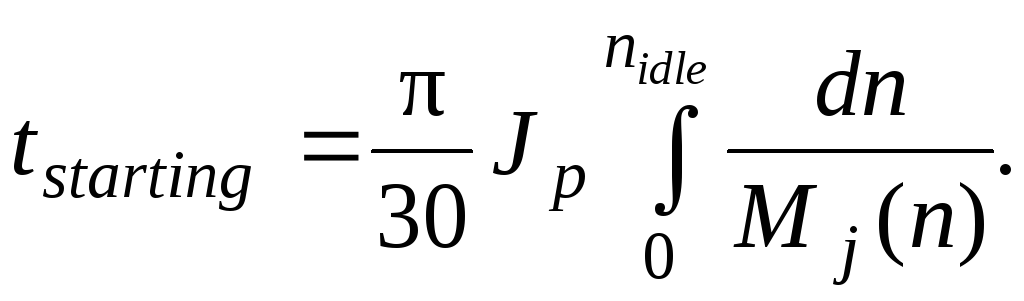
According to the third Newton’s law the moment of inertia forces, which counteracts to accelerated rotation of the rotor, should be overcome by supply of redundant torque to the rotor (concerning the requirement of uniform rotation).
The redundant torque can be determined, using the starting diagram (see Fig.14.3), with the help of such formulas:
- for the first stage of starting Мj I (n) = МSD – МR ;
- for the second stage of starting Мj II (n) = МSD + МТ – МR;
- for the third stage of starting Мj III (n) = МТ – МR .
The diagram of the redundant torque is shown in Fig. 14.8.