3. Алгебраїчні конгруенції -го степеня за складеним модулем

Теорема. Якщо – канонічний розклад модуля 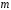на множники, то алгебраїчна конгруенція 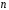-го степеня за складеним модулем

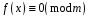, (4)

еквівалентна системі конгруенцій

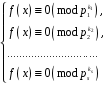(5)

і число розв’язків конгруенції (за 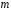модулем ) (4) дорівнює добутку чисел розв’язків конгруенцій (5) (кожен з розв’язків за відповідним модулем).

Можливі наступні випадки розв’язування конгруенції (4):

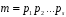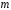1. Модуль конгруенції (4) має лише прості множники . Якщо відповідна система (5) сумісна, то число розв’язків конгруенції (за модулем ) (4) дорівнює добутку чисел розв’язків конгруенцій (5) (кожен з розв’язків за відповідним модулем). Розв’язуючи систему (5), розв’яжемо спочатку кожну конгруенцію окремо, потім знайдені розв'язки скомбінуємо між собою.

2. Модуль конгруенції (5) має вигляд , де 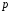– просте число.

Спочатку розв’яжемо конгруенцію за простим модулем

.

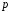
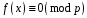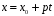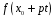Припустимо, що вона має розв'язки , де . Розкладемо функцію у ряд Тейлора:

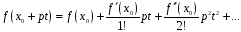
Усі члени даного ряду, починаючи з третього, діляться на 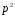. Отже, конгруенція має місце при

.

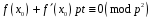Значення 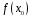ділиться на , тому що 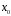– розв'язок конгруенції за модулем . Із знайденої конгруенції легко визначити 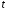за умови, що 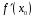не ділиться на :

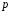Розв’язком останньої конгруенції бу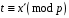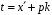де , , де 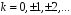. Тоді

,

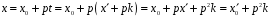де . В результаті . Підставимо це значення замість 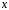в даний многочлен і знову розкладемо функцію 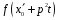у ряд Тейлора:

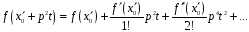
Усі члени даного ряду, починаючи з третього, діляться на 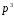. Звідси випливає, що весь многочлен ділиться на 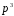тоді, коли вираз 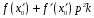ділиться на 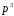. Отже, конгруенція має місце при

.

Значення 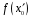ділиться на 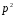, тому що 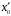– розв'язок конгруенції за модулем 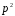. Із знайденої конгруенції легко визначити 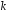за умови, що не ділиться на :

.

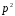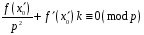Розв’язком останньої конгруенції бу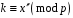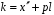де , , де 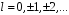. Підставивши це значення у вираз для 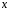, дістанемо загальний розв'язок за модулем :

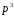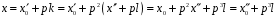
де .

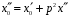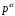Продовжуючи аналогічним чином, дійдемо до конгруенції за модулем , тобто дістанемо розв'язок вихідної конгруенції за цим модулем.

4. Алгоритм Берлекемпа розкладання многочлена на незвідні множники над скінченним полем

Нехай 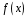– нормований, вільний від квадратів многочлен степеня 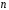над полем . Для розкладання його на незвідні над полем 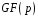множники застосовується алгоритм, запропонований Е. Берлекемпом.

1. Побудувати матрицю порядку

,

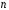
рядки якої є коефіцієнтами многочленів-лишків за модулем . Перший рядок цієї матриці завжди являє собою коефіцієнти многочлена 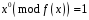, тобто 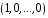, другий рядок являє собою коефіцієнти многочлена 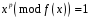, третій – 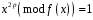, останній – . Щоб знайти коефіцієнти цих многочленів, треба побудувати множину лишків за модулем 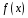для степенів , .

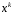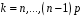2. Побудувати матрицю 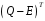і знайти базис простору розв’язків системи лінійних алгебраїчних рівнянь 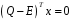. Нехай 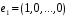, , 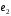…, 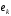– знайдений базис.

Зауваження. Оскільки перший рядок матриці 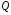(7) є 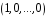, то перший стовпець матриці 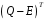буде нульовим. Тому вектор 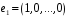завжди буде базисним.

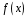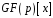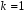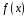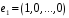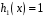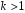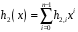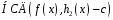3. Число знайдених базисних векторів дорівнює числу незвідних дільників многочлена в . При многочлен незвідний, вектору відповідає сталий многочлен . При треба взяти базисний вектор і побудувати многочлен . Обчислюючи для всіх , знайти розклад на множники, де , .

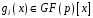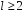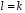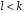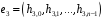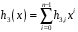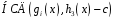Якщо , то алгоритм зупиняється. Якщо , то треба взяти базисний вектор , побудувати , обчислюючи для вже знайдених множників 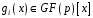, знайти подальший розклад 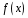, і т.д., доки не знайдемо всі 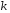множників.

Алгоритм зупиняється, коли знайдений розклад многочлена на 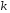множників, де .
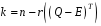