39

Т е м а 2 Электромагнитные колебания в регулярных волноводах и резонаторах без потерь

2.1. Классификация линий передач

Направляющей системой, волноводом или линией передачи (ЛП) электромагнитной энергии называют совокупность тел, осуществляющих передачу электромагнитной энергии в определенном направлении без излучения в окружающее пространство.

Линии передач называют регулярными, если их свойства вдоль направления распространения неизменны или меняются по периодическому закону. В первом случае ЛП называется продольно-однородной, во втором - периодической.

Если электромагнитное поле ЛП не ограничено в поперечном направлении, то её называют открытой. В закрытых ЛП электромагнитное поле существует только внутри замкнутой металлической оболочки.

В соответствии с материалом тел, образующих ЛП, их делят на металлические, диэлектрические и металлодиэлектрические.

Свойства ЛП существенно зависят от связности их поперечного сечения. Если любой контур, расположенный в сечении ЛП, можно стянуть в точку, не пересекая границу раздела металл-диэлектрик, то ЛП называют односвязной. В противном случае ЛПмногосвязная, причем степень связности соответствует числу различных типов контуров, которые можно выделить в её поперечном сечении.

Примеры основных типов ЛП показаны на рисунке 2.1.

а б в

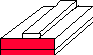
г д

Рис 2.1. Основные типы линий передач : а - закрытая металлическая односвязная , б - закрытая металлическая двусвязная , в - открытая диэлектрическая односвязная , г - открытая металлодиэлектрическая двусвязная, д - периодическая ЛП.

2.2. Общие свойства электромагнитного поля в регулярных волноводах с идеально проводящими стенками

Рассмотрим регулярный волновод с произвольным контуром сечения L ,

идеально проводящими стенками и вакуумом внутри. Источников нет (рис.2.2).

x z

y J_e = 0

L Рис. 2.2.

Согласно принципу поляризационной двойственности поле внутри волновода равно :

Е = Е_e + E_h , H = H_e + H_h . (2.1)

Рассмотрим первую возможную реализацию волновых процессов, описывающихся с помощью однокомпонентного вектора Герца П_e(0,0,П_ez ) .

Векторное волновое уравнение для П_e в этом случае переходит в скалярное волновое уравнение для его компоненты :

 ²П_ez /x² +  ²П_ez /y² + ²П_ez /z² + k²П_ez = 0 . (2.2)

При решении (2.2) воспользуемся методом Фурье :

П_ez(x,y,z) = (x,y) q(z) . (2.3)

Из (2.2) и (2.3) имеем :

(1/)( ² /x² +  ² /y²) +(1/q)(d²q /dz²) + k² = 0 (2.4)

Сумма двух функций, зависящих от разных переменных, может быть равна константе только в том случае, кода обе функции являются константами.

 ² /x² +  ² /y² + æ² = 0 , (2.5)

d²q/dx² + h²q = 0, (2.6)

æ² + h² = k² , (2.7)

h - продольное волновое число, æ - поперечное .

Уравнение (2.6) имеет решение q = Aexp(ihz) + Bexp(-ihz) , (2.8)

представляющее собой наложение двух волн, распространяющихся вдоль оси z . Первое слагаемое есть функция от комбинации (hz-t), второе - от комбинации (hz + t).

Величина ( hz  t ) называется фазой волны. Фиксированное значение этой величины позволяет определить направление и скорость распространения волнового процесса. Если (hz - t) = const, то это процесс, движущийся по направлению оси z.

Если (hz + t) = const, то это процесс, движущийся против направления оси z.

Скорость распространения обоих процессов ( её называют фазовой скоростью волны и обозначают _ф ) определяется из уравнения :

(hdz  dt) = 0. Иначе : _ф = dz/dt =  /h (2.9)

Принимая вышесказанное, найдём компоненты векторов Е и Н :

Е = rotrot{П_е(х,y)exp(ihz)}, H = -i₁rot{П_е(х,y)exp(ihz)}, (2.10)

Е_ex = ih(П_e /х)exp(ihz), E_ey = ih(П_e/y)exp(ihz), E_ez = æ2П_e exp(ihz), (2.11)

Н_ex = -i₁(П_e/z)exp(ihz) , H_ey = i₁(П_e /z)exp(ihz) , H_ez = 0 (2.12)

Определим граничные условия для П_е(x,y) . Тангенциальная составляющая электрического поля на поверхности стенок равна нулю :

Е_et /s = 0. (2.13)

Вводя правую тройку векторов s , n , z, по аналогии с (2.11) имеем :

Е_es /s = ih(П_e /s)exp(ihz) = 0 , E_ez /s = æ²П_е exp(ihz) = 0 . (2.14)

Таким образом, из (2.14) видно, что если

Е_ez = Е_es = 0 , то П_е/s = 0. (2.15)

Итак, задача нахождения ТМ-поля свелась к следующей :

П_ez (x,y,z) = П_e(x,y) exp(ihz),

²П_е/x² + ²П_е/y² +æ²П_е = 0, (2.16)

П_е/s = 0 , æ² + h² = k² .

Формулировка (2.16) известна в математической физике под названием внутренней задачи Дирихле. Отличные от нуля решения этой задачи возможны лишь для спектра собственных значений æ²_n . Каждому собственному значению æ²_n соответствует собственная функция П_еn(x,y) и два значения волнового числа h_n = ± (k² - æ²_n)^1/2. Величина h²_n может быть как положительной, так и отрицательной (в зависимости от величин к² и æ²_n). При h²_n  0 в волноводе существует незатухающий волновой процесс П_en , распространяющийся вдоль оси z. При h²_n  0 волновой процесс П_en экспоненциально затухает. Частоты _n , при которых k = æ_n и h_n = 0 , называются критическими частотами :

_nкр = æ_n/(₁₁)^1/2 . (2.17)

Каждой критической частоте _nкр в свободном пространстве соответствует

критическая длина волны

_nкр=2/æ_n, (2.18)

определяющая границу распространения волнового процесса П_en в волноводе . Именно : вычисление z компоненты вектора Пойтинга :

S_kz =(1/2)Re{[E,H^]_z} =

= (1/2)Re{ih(П_е/х)exp(ihz)(-i₁)(П_е/х)exp(-ihz) - ih(П_е/y)exp(ihz)

(i₁)(П_е/y)exp(-ihz)} = (1/2)₁{(П_е/х)² + (П_е/y)²}Reh (2.19)

показывает, что

при h²_n  0 , S_kz  0 , при h²_n  0 , S_kz = 0 . (2.20)

Это означает, что при   _nкр , или   _nкр , переноса энергии по волноводу нет и имеются лишь отражения волн от стенок в плоскости, перпендикулярной оси распространения (так называемые местные волны ).

Волны, распространяющиеся по волноводу имеют определённые значения длины волны (_n) и фазовой (_фn) скорости, связанные с  и _nкр следующими соотношениями :

_n = 2/h_n = 2/[(2/)² - (2/_nкр)²]^1/2 = /[ 1 - (/_nкр)² ]^1/2 , (2.21)

 = 2/k = 2/(₁₁)^1/2 = 2C/ , C = 1/(₁₁)^1/2 , (2.22)

_фn = /h_n = /[(2/)² - (2/_nкр)²]^1/2 = C/ [1 - (/_nкр)²]^1/2. (2.23)

Таким образом, _n   , _фn  C , т.е. фазовая скорость волны в волноводе больше скорости света (что, впрочем, не противоречит теории относительности, так как фазовая скорость не является характеристикой распространения энергии).

Здесь следует напомнить, что помимо фазовой скорости распространения волны, в общей электродинамике существует понятие групповой скорости волн. Последнее связано с тем, что реальные электромагнитные волны не являются монохроматическими, хотя бы уже потому, что они всегда имеют ограниченную протяженность в пространстве и ограниченную длительность во времени. Такие волны могут быть представлены в виде совокупности монохроматических волн и называются группой волн, или волновым пакетом. В диспергирующих средах (т.е. таких, где значение фазовой скорости зависит от частоты) происходит искажение формы группы волн в процессе её распространения, обусловленное различием фазовых скоростей отдельных монохроматических компонент группы. Для характеристики распространения такого процесса понятия фазовой скорости уже недостаточно, и поэтому понятие групповой скорости вводится как характеристика распространения огибающей волнового пакета. В отсутствии потерь (а также когда они малы и слабо зависят от частоты) групповая скорость совпадает со скоростью распространения энергии. В противном случае (большие потери и сильная зависимость от частоты) понятие групповой скорости теряет смысл. Пользуясь известным из общей электродинамики выражением для вычисления групповой скорости _гр = d/dh найдём, что

_грn = d/dh_n = d/d{[(2/)² - (2/_nкр)²]^1/2} = [(2/)² - (2/_nкр)²]^1/2d/d(2/) =

= C [1 - (/_nкр)²]^1/2 < C , _фn _грn = C² . (2.24)

На этом этапе мы рассмотрели первую возможную реализацию класса волновых процессов, описываемых при помощи вектора П_е (Е волны).

Теперь рассмотрим реализацию, описываемую при помощи вектора П_h ( H волны ).

Здесь можно было бы также записать волновое уравнение для компоненты П_hz и решить его методом Фурье , но в этом нет необходимости, если вспомнить принцип перестановочной двойственности и провести замену :

Е_е  -(₁/₁) H_h , H_e  E_h .

Единственная разница заключается в граничных условиях для П_h(x,y) .

Именно : нам нужно удовлетворить условию Е_ = 0  E_z/s = E_s/s = 0 . (рис.2.3)

s z

J_e = 0

n

S

L Рис. 2.3.

Поскольку E_h = -i rotП_h , H_h = rot rot П_h , то отсюда имеем :

Е_hz  0 , E_hs = -i(П_h/n) exp(ihz) = 0  (П_h/n)/s = 0 . (2.25)

Таким образом, задача нахождения волнового процесса, описываемого магнитным вектором Герца, свелась к внутренней задаче Неймана :

П_hz (x,y,z) = П_h(x,y) exp(ihz) ,

²П_h/x² + ²П_h/y² +æ²П_h = 0 , (2.26)

(П_h/n)/s = 0 , æ² + h² = k² .

Решение для П_h , как и решение для П_е также возможно лишь для спектра собственных значений æ_n и обладает теми же общими свойствами, что и решение для П_е . На этом этапе перейдём к рассмотрению конкретных сечений (типов) волноводов.