69. Сферические функции

Полиномы Лежандра и их свойства

Рекуррентная формула позволяет вычислить полиномn+1 степени, если известны значения полиномовn иn-1 степеней

(4.1)

Производящая функция полиномов Лежандра используется в представлении потенциала притяжения рядом по сферическим функциям. Она имеет вид

(4.2)

Ортогональность сферический функций

Ортогональность полиномов Лежандра определяется формулой

(4.3)

где - символ Кронекера. Присоединенные функции Лежандра также обладают свойством ортогональности. Из теории специальных функций известно, что

(4.4)

Сферические функции также образуют класс ортогональных функций. Докажем свойство ортогональности сферических функций. Возьмем две шаровые функции первого рода 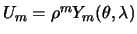и. Применим к ним вторую формулу Грина для сферы. Учитывая, что, формула Грина принимает вид

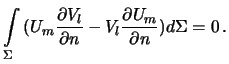(4.5)

Для сферы производная по нормали совпадает с производной по радиус-вектору ᵨ, поэтому

Подставляя полученные выражения в формулу (4.5), будем иметь

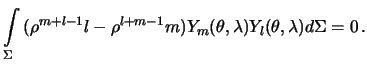Поскольку радиус-вектор -- постоянная величина, полученное выражение можно переписать в следующем виде

(4.6)

При приведенный интеграл равен нулю, что указывает на ортогональность сферических функций.

Вернемся теперь к сферическим функциям степени , заданной в общем виде

(4.7)

Функции вида

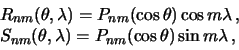(4.8)

называются сферическими гармониками. Очевидно, что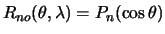,. Можно показать,что

(4.9)

Все основные выкладки можно найти в учебниках по специальным функциям.

Нормированные сферические функции

Как мы видели, средние значения квадратов сферических гармоник достаточно сложно выражаются через постоянныеm и n. Однако, каждую из гармоник можно умножить на постоянные так, чтобы интегралы в формулах (4.9) были равны единице. Эта операция называется нормировкой. Обозначая чертой сверху нормированные функции, можно записать

где - нормировочный множитель. Выберем его так, чтобы выполнялись равенства

(4.10)

Обращаясь к формулам (4.9) легко устанавливаем, что

Полученную формулу можно переписать следующим образом

(4.11)

Операции нормировки подвергают не только сферические гармоники, но и полиномы и функции Лежандра. В частности, если нормированная сферическая функция имеет вид

(4.12)

то

70. Применение специальных функций.

Специальные функции используются для решения уравнений с частными производными, например, метод разделения переменных в цилиндрических и сферических координатах приходим к цилиндрическим и сферическим функциям.

Одна из характерных особенностей этих функций состоит в том, что как правило, являются решением уравнения: с особыми точками, т.е. коэффициент обращается в нуль в одной или нескольких точках промежутка изменения переменной. Решение таких уравнений имеет ряд специфических свойств. Также используются для решения многих задач в физике, математике и технике.