40. Задачи с данными на характеристиках.

Понятие характеристик для уравнения позволяет найти существенно новое явление описываемое этим процессом. Рассмотрим уравнение: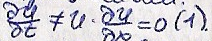

Уравнение характер. имеет вид: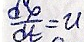значит в левой части уравнения (1) диффер. прошло вдоль характер.Поэтому (1) можно записать в видегдеr- искомая характеристика. Поэтому вдоль этой характер. Функция принимает постоянные значения. Рассмотрим задачу КошиЕсли фи имеет видто на участке [0;X1] характер. Будет расходиться так как угловые коэффициенты растут, а на участке (Х1 Х2) характер. Сходиться т.к. угловой коэффициент убывает с ростом Х,а значит характеристики пересекутся в некоторой точке (t0 x0). Однако функция U на каждом характер. примет своё постоянное значение .Поэтому в точке пересечения (t0 x0) иметься 2а значения U чего быть не может.По этому в этой точке частная производная уходит в бесконечность.

41. Метод Римана решения задачи Коши для гиперболического уравнения на плоскости.

Пусть Gобозначает треугольную область, ограниченную характеристиками ε=и 𝝶=и отрезком гладкой кривой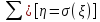. Для определенности считаем , что кривая ∑ проходит через точки () и (). Предполагаем что кривая ∑ нигде не касается характеристик , т.е.<0, 0≤𝝽≤. Поставим задачу Коши для уравнения в областиG. Найти функцию U(x,y), Uϵ, , удовлетворяющих уравнениюLu=+a(1) вGи данным Коши на ∑ :.

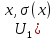Теорема: Если ∑-кривая класса , функцииa,b,c,принадлежат С(),fϵC(),и]ϵ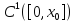, торешение задачи Коши существует, единственно и выражается формулой Римана

U(x,y)= , где - части областиGи кривой ∑, лежащие между характеристиками 𝝽=xи 𝝶=y ; y=𝞂(,.

Отметим некоторые качественные следствия , вытекающие из формулы Римана. Из этой формулы видно, что решение задачи Коши в точке (x,y) полностью определяется значениями данных f,в замкнутой треугольной области-области зависимости точки (x,y). Поэтому если эти данные изменять вне фиксированной области( с соблюдением надлежащих свойств гладкости), то т решение будет меняться лишь вне этой области. Таким образом , мы приходим к следующему выводу: к данному решению задачи Коши зафиксированному в области, можно присоединить вдоль характеристик𝝽=x* и 𝝶=y*, вообще говоря , различные решения, являющиеся его продолжением.

42.Уравнение распространения тепла.

Пусть функция u(t,x) определяет поле температур в точке x(x₁, x₂,x₃) в момент времени t. Будем считать среду изотропной. Обозначим ρ(x), c(x), k(x) ей плотность, теплопроводность и коэффициент теплопроводности в точке x соответственно. Пусть F(t,x) – интенсивность источников тепла в точке x в момент времени t. Выделим некоторый объём V и подсчитаем баланс тепла за промежуток времени (t;t+t). Пусть S- граница объёма V, -внешняя нормаль к этой границе. Соответственно закону Фурье, через поверхностьS в объём V поступает количество тепла:

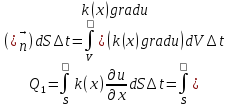
От тепловых источников выделяется количество тепла в объём V.

Для этого изменения температуры необходимо затратить количество тепла:

По закону сохранения энергии:

Откуда в силу произвольности выбора объёма V получаем равенство подынтегральной функции:

, которое относится к параболическому типу. В случае, когда среда однородная, параметры c, ρ и k – постоянные:

Где 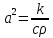,. Это уравнение теплопроводности. При выводе уравнения теплопроводности рассматривали пространственный случай, когда количество пространственных переменных равно 3. Вообще говоря, их в уравнении теплопроводности может быть сколько угодно.