50. Понятие обобщённого решения для уравнения с частными производными.

П1.Основные ф-ции. Пусть множество Ω отсутствует: Опр1: Ф-цияf(x)не=0, Vх€Ω; f(x)=0, Vx€Rⁿ- Ω-наз.финитной. Замкнутое множество Ω наз.

Финитной множества f: Ω=Suppf .

f_xесли выполняются след. условие:

1. F_k(x)→f(x)

2. D^Jf₀(x)→D^Jf(x) , D^J=d^J/dx^J,dx_2....dx_n^Jn

3. Сущ. ограниченное множество :ΩᴄRⁿ,Suppf*ᴄΩ,VkᴄN, SuupfᴄΩ

Пространство D, Rⁿcуказанной сход.будет наз. с пространством основных ф-ций.

П.2 понятие обобщённых ф-ций .

Рассмотрим некоторую линейную ф-циюf действующую f€D (Rⁿ) f-линейный ф-онал.

П.3 Регулярные обобщенные ф-ции .

Рассмотрим, произвольную, интегрируемую ф-циюg. На её основании постоим, линейный ф-нал g€Dˡ(Rⁿ)

(g,f)= ∫g(x)f(x)dxпроверим условия непрерывности функционала: Придельный переход под знаком интеграла возможен в силу равномерной сходимости, последовательностейf.

П4. Фундамент решения дифф.ур-ния.

Рассмотрим произвольноеур-ние порядка n:

Σa(x)D^JИ=f (3)

Длялюбой ф-цииfиз пространства основных ф-ции

L[И]=Σа(х) D

L*[v]=Σ(-1)^J(-1^J)D^J(a(x)v),

если в качестве первой части взять ур-ние Дирака, то получим L[и]=δ_Χ

Естественно, что обобщённая ф-ция оператора обозначается не однозначно. Учитывая прикладной характер ур-нения .

51. Уравнение Лапласа. Формулы Грина.

Ур-ние Лапласа.

Введем n- мерный оператор Лапласа: А_n=d²/dx²+d²/dx²₂+.....+ d/dx_n², И=0,

Оно приводится к эллиптическому типу и описывает различного рода стационарные процессы: форму мембраны устоявшееся поле температур, потенциал поля притяжения.

Ур-ниеПуассона. Опред.1.Ф-ция И наз. Ограниченной области Ω если она в этой области имеет непрерывные производные до 2-ого порядка включительно и удовлетворяют ур-нию Лапласа во всех областях Ω.

Опр.2. И(М)→0

И(x,y,z)=(3.)

М₀()-не является решением.

Ф-ция наз. Фундаментальным решением трехмерной

ур-нияЛапласа. Ф-ция

И(x,y)=

Удовлетворяет, двухмерномуур-нию Лапласа и наз. Фундаментальным решением двумерного ур-ния Лапласа.

П2. Формула Грина. Ф-ла Грина, выводится на основании ,ф-лы Остроградского связаны тройные и поверхностные интегралы. ΩᴄR³ограничена кусочно-гладкой ориентированной поверхности S и пусть р, g, R имеет w:

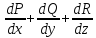∫∫∫()dV=∫∫Pcos(n^˄,x)+Qcos(n^˄,y)+Rcos(n^˄,z)ds

В формуле Остроградского положим:

P=и;Q= и;R= и;тогда:

∫∫иds-∫∫∫и - первая ф-ла Грина.

∫∫∫(и)=∫∫(u)ds- вторая ф-ла Грина.

Заметим, что первая и вторая ф-ла Грина, могут быль применены и тогда когда Ω ограничена несколькими замкнутыми областями в этом случае поверхность интегрирована необходимо брать по всем областям ограниченным Ω.

Лемма. Пусть ф-ция и непрерывна и имеет непрерывные производные 1-ого порядка на области Ω и непрерывны вплоть до ее границеS:

u()=-

r=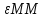₀ǀ, M₀(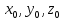)- лежащий в области Ω.

n- внешняя нормаль поверхностиS.

Вначале предложим, что ф-ция И имеет непрерывная производная 2-ого порядка на границе S.

dv=-

52. Общие особенности гармонических функций.

Будем исходить из формулы Гаусса-Остроградского

Справедливой для кусочно-гладкой поверхности, ограничивающей область Ω.- векторное поле,- вектор нормали к поверхности.

Пусть функции u и v имеют непрерывные вторые производные в Ω и непрерывны вместе с первыми производными в ее замыкании .

Положим , тогда:;

где.

Поэтому из формулы (1) с учетом получим :.

Это - первая формула Грина.

Меняя в формуле (2) u и v местами, получим : .

Вычитая равенства (2) и (3) почленно, находим : .

Это - вторая формула Грина.

Наконец, полагая в (2) u = v, получим : .

Это - третья формула Грина.

Здесь всюду- вектор внешней нормали к гладкой или кусочно-гладкой замкнутой поверхности.

Замечание: Граница области Ω может состоять из нескольких замкнутых поверхностей. В этом случае поверхностные интегралы в правых частях формул Грина следует брать по всем поверхностям, ограничивающим область Ω.