1. Тригоном. Сист ф-ций. Тригоном ряд Фурье.

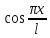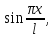
Опр.1.систему ф-ций 1/2, , , 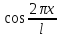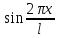…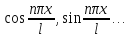(1) - наз тригоном системой ф-ций.

Для системы ф-ций (1) справедливо св-во ортогональности.

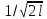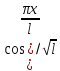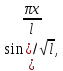
Св-во1: тригоном ф-ция (1) ортогональна на отрезке [-l,l]. Квадрат нормы тригоном сист (1) равен l, а первой ф-ции l/2, поэтому из (1) получают др системы ф-ций (2): ,, , 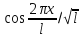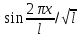…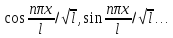кот явл нормированной на отрезке [-l,l].

Из св-ва 1 вытекает св-во 2: тригоном ф-ция (2) ортонормированна на отрезке [-l,l].

Тригоном ряды Фурье:

Опр1. Функциональный ряд вида 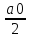(1): +a1

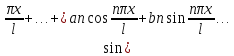
где aiєR, bjєR, iєN0, jєN будем наз тригоном рядом.

Более кратко тригоном ряд (1) запис в виде: .a0,an,bn – коэф-ты тригоном ряда.

Будем считать, что 2l периодическая ф-ция f представляется тригоном рядом (1) на интервале [-l,l], т.е. : f(x)=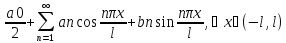(2)

Будем считать, что для тригоном ряда стоящего в правой части (2) выполняются все условия о почленном интегрировании.

Выразим коэф-ты ряда (2) через саму ф-цию f, для этого проинтегрируем ф-цию по отр (-l,l):

,

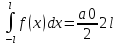
(3)

для нахождения an умножим (2) на 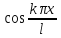и проинтегр по отр (-l,l):

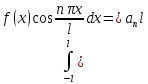
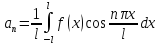- (4)

для нахождения bn умножим (2) на 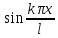и проинтегр по отр (-l,l):

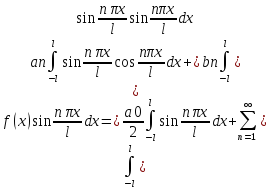
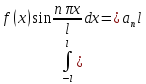
bn=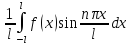- (5)

метод нахождения (3-5) – метод Эйлера-Фурье.

Опр2: ф-лы (3-5) – ф-лы Эйлера-Фурье ф-ции f.

Опр3: коэф a0,an,bn вычисленные по ф-лам Эйлера-Фурье наз коэф-ми Фурье заданной ф-ции f.

Опр4: тригоном ряд, коэф-ты кот явл коэф-ми Фурье ф-ции f наз тригоном рядом Фурье или просто рядом Фурье ф-ции f

2. Ряд Фурье по ортогон-й системе элементов гильбертова пр-ва. Неравенство Бесселя.

Рассм-м гильбертово пр-во ф-ций L2[a;b] – пр-во ф-ций интегрируемых вместе со своим квадратом на отр [a;b].

В этом пр-ве ф-ции введем скалярное произвед-е (f,g)=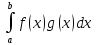, тогда норма ф-ции f вводится:

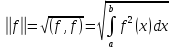
В данном гильб-м пр-ве L2[a;b] выберем ортогон систему ф-ций: 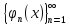- (1)

Ортогон-ть означает: 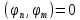, n≠m, n,mєN

Будем считать, что в сиситеме ф-ций (1) нет нулевых, это значит, что 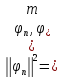- (2)

Замечание: если 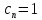при всех натуральныхn. То сист ф-ций (1) будет ортонорм-й. В противном случае ее можно нормировать и рассм-ть сист

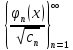
Поставим задачу об разложении опр ф-ции f на отр [a,b] в ряд по сист ф-ций (1). Это значит нам необходимо найти коэф разложения (3): f(x)= 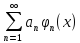- (3)

Воспользуемся методом Фурье - умножим на 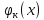и проинтегр на [a;b]: ,

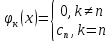учитывая св-во ортогон-ти и (2) т.о. имеем: ,

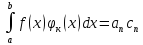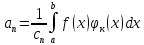
Учитывая (2): 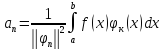- (4)

Опр1: Ряд (3) по ортогон сист ф-ций (1) гильб пр-ва L2[a;b] коэф-ты кот находящийся по ф-ле (4) наз обобщ-м рядом Фурье ф-ции f. Сами коэф-ты an- обобщ коэф Фурье.

Неравенство Бесселя.

Т1. Пусть ф-ция f из пр-ва L2[a;b]. - ортогон сист ф-ций пр-ва L2[a;b]. Тогда длю коэф Фурье ф-ции f по ортогон системе выполняется неравенство Бесселя:

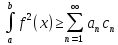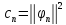, где - (1)

В обозначениях нормы неравенство Бесселя (1) запис в виде:

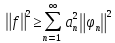
Док-во: исп-я св-во ортогон-ти для m-х частичных сумм ряда Фурье ф-ции f имеем:

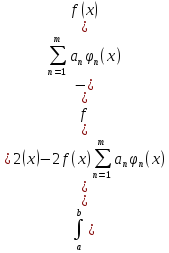
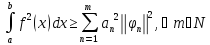
Последнее неравенство означает, что все частные суммы ряда Фурье ограничены сверху квадратом нормы ф-ции f. Поэтому данный числовой ряд сх-ся, а его сумма не превосходит квадрат нормы ф-ции f. Т.е. неравенство Бесселя верно, т-ма док-на.

Для тригоном систем ф-ций неравенство Бесселя принимает вид: