реалогия мустафина

кейін де деформация байқалады. Үшінші денелер – ағады, яғни деформация ұдайы күштің әсерінен тоқтаусыз өседі.

Реологиялық құбылыстар механикалық процестер болғандықтан, реологияда механиканың негізгі заңдары қолданылады:

F арқылы күш векторын, ал a - жылдамдату векторын өрнектесек,

онда

мұндағы: å белгісі векторлық сумманы көрсетеді, сондықтан

åF - денеге әсер ететін барлық күштің нәтижесі; m – масса;

а0 - жиын центрі жылдамдатуы;

Егер åМ =åFr қозғалмайтын нүктеге қатысты нәтиже моменті деп алсақ (мұндағы r – осы нүктеге қатысты күш иығы), онда

мұндағы формуланың оң жағындағы интеграл бүкіл бөлшектерге қатысты, а - dm массалы бөлшектің жылдамдатуы; r – қозғалмайтын нүктеден жылдамдатуға дейінгі түзудің арақашықтығы.

Егер моменттер дене массасы центріне қатысты есептелсе, онда (1) теңдеуі массалар центрі тынышталмаған кезде ғана тура болады, яғни бұл жағдайда басы масса центрімен сәйкес келетін және үнемі бірге қозғалғанда салыстырмалы қозғалыстағы координат жүйесіне жылдамдату болып табылады.

(1) және (2) теңдеулері келесідей түрде жазылуы мүмкін:

(4)

(x,y,z) жазуы өзі жасалған теңдеудің құбылыстың мағлұматтарын сипаттайтын үш теңдеулер жүйесінің бірін көрсететінін сипаттайды. Мұндағы теңдеудің индекстері айналмалы алмасуға тиісті: z-ті х-ке, х-ті у-ке және у-ті z-ке. Мысалы, (4) теңдеуден келтірілген ауыстыру арқылы алынған теңдеудің түрі:

åM х =å(Fz x -Fz y) = ò(az x -ay z)dm

(5)

Егер бір ғана бөлшекті немесе «материалдық нүктені» қарастырсақ, онда теңдеулер мынандай түрге келеді:

21

Бұл теңдеу Ньютонның І-ші және ІІ-ші заңдарын көрсетеді. (1.3) және

(2) теңдеулері а немесе r кинематикалық шамалары және F , M динамикалық шамалары арасындағы арақатынасын береді.

Бұл шамалар өзара массалар арқылы байланысқан V - дененің көлемі және dv – дене бөлшегінің көлемі болсын, онда

Бұл шама заттың тығыздығы деп аталады және денені құрайтын затты сипаттайтын шама болып табылады. (1) және (2) теңдеулеріне (7) теңдеуінен m массасын енгізу арқылы механика теңдеулеріне кіретін заттың жалғыз параметрі болатын тығыздық арқылы кинематикалық және динамикалық шамалар байланысатынын көреміз.

Реологияда әртүрлі заттардың реологиялық жүрісін сипаттайтын заттың константасы болып келетін параметрлер арқылы деформация деп аталатын кинематикалық шаманы кернеу деп аталатын динамикалық шамамен байланыстыратын теңдеулер негізгі теңдеулер болады.

Бақылау сұрақтары?

1.Ығысу деформациясы дегеніміз не?

2.Реологиялық механика неге байланысты?

3.Ағымды деформация дегеніміз не?

ДӘРІС №4 Реологиялық кинематика. Реологиялық динамика

Дененің кинематикалық жағдайы оның барлық бөлшектерінің уақыттың әрбір моментіндегі жылдамдығымен және күйімен анықталады.

Бөлшектің күйі оның х, у, z координаттарымен математикалық түрде сипатталады, ал оның жылдамдығы мына компоненттер арқылы өрнектеледі:

Сондықтан t моментіндегі кинематикалық күйді анықтау үшін алты шама енгізу қажет. Дене саны шексіз көп бөлшектерден тұратындықтан, «алты еселі шексіз» санды енгізу керек болып көрінуі мүмкін. Алайда, бұл жағдай тек қана дене бөлшектері бір-бірінен тәуелсіз болған кезде ғана болады, ал мұндай бөлшектер дене құрай алмайды. Бөлшектер t уақытында және t уақытынан кейін де жақын тұрған кезде ғана дене құрайды.

22

Сондықтан, егер біз (х, у, z) және (x+dx, y+dy, z+dz ) координаттарымен екі бөлшекті қарастырсақ, онда олардың жылдамдықтарының бағыты бойынша айырмашылығы да шексіз аз шама болады.

Басқа сөзбен, бөлшектердің жылдамдықтары координаттардың үздіксіз функциялары болады.

t уақытының шамалы созылуын қарастырайық. Бұл уақыт аралығында әрбір бөлшек өзінің күйін ығысу деп аталатын u шамасына өзгертеді.

Мұнда жылдамдықты төмендегідей табамыз:

Егер жылдамдық координаттардың үздіксіз функциясы болса, онда ығысу да осы координаттардың үздіксіз функциясы болуы керек. Сондықтан берілген бөлшектен көршісіне өткенде олардың ығысу айырмашылықтары мына шамаларға (х координаты үшін) тең болады:

Осылайша у және z осьтері бойынша ығысу үшін де өрнек жазуға болады.

Белгілі бір бөлшектен келесі бір бөлшекке S бағытта өткенде:

Бұл шама тоғыз санмен де табылуы мүмкін:

23

Мұндай шама тензор деп аталады. Тензор деформацияның нақты шамасы және реологиялық кинематикалық шама бола алмайды. Жеңіл өзгертулер арқылы тензорды деформация тензорына келтіруге болады.

(1.8)

(1-3) тензоры негізгі реологиялық кинематикалық шама болып табылады.

ε×xx және т.б. шамалар деформация тензорының компоненттері деп аталады.

Реологиялық динамика

Дененің ішінен шекті тұйықталған бет арқылы ойша бөлшек бөліп аламыз.

24

Осы бет арқылы бөлшекке қалған бүкіл дене әсер етеді, ал бөлшек Ньютонның үшінші заңы бойынша дененің қалған бөліктеріне әсер етеді. Ойша алынған шекті беттің элементін қарастырайық. Оның ауданын S , ал кеңістіктегі ориентациясын қарастырып отырған беттің элементіне сыртқы нормальдің n бағыты деп белгілейік (1 сурет).

pn - беттік күштің шамасы, онымен дененің қалған бөлігі бөлшекке

кернеуі деп атаймыз. Кернеу векторлық шама және ол беттің элементінің алаң ориентациясына байланысты болады.

pn беттік күшінің кернеуі жалпы жағдайда n нормалімен бұрыш құрайды және pnn мен pnt (нормаль және жанама) компоненттеріне жіктелуі мүмкін.

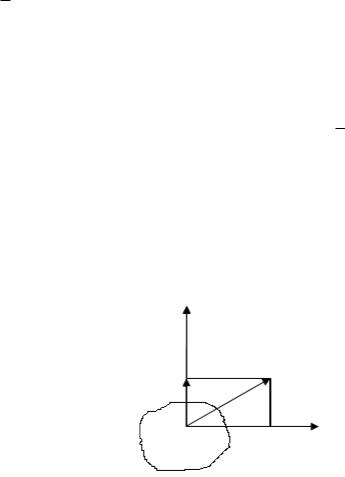
Тікбұрышты параллелепипед пішінді қарапайым бөлшекті қарастырайық (2 сурет).

Алаң ориентациясы кез келген болуы мүмкін, сондықтан беттің нүктесіндегі қызу (напряженный) күйінің шексіз көп берілу әдістері бар болып көрінуі мүмкін.

1сурет. Ойша алынған шекті беттің элементіне әсер ететін күштің жоспары.

Бірақ А нүктесі арқылы өтетін өзара үш перпендикулярлы кез келген алаңдағы кернеу векторларының компоненттерін беру арқылы дененің кез келген нүктесіндегі қызу күйді толығымен анықтауға болады (2-сурет).

25

2 сурет. Тікбұрышты параллелепипед пішінді қарапайым бөлшектің кернеулері.

Қызу күйді сипаттау үшін әрбір вектор үшін үш-үштен, барлығы тоғыз кернеу компонентін білу қажет. Ыңғайлы болу үшін әрбір компонентті і және j индекстерімен жазуға болады.

Бірінші индекс нормальдің алаңға бағытын, ал екіншісі күш әрекетінің бағытын көрсетеді.

Мысалы, τyz - у осіне перпендикуляр алаңда z осі бағытында әсер ететін күш. Сондықтан, (1.4) және (1.6) теңдеулерінен тоғыз компонентті σij кернеу тензорының бар екендігін көреміз.

мұндағы σxx ,σyy ,σzz - нормальді кернеулер;

τxy ,τxz және т.б. – жанама кернеулер;

Осылайша, σij кернеу тензоры реологиялық динамикалық шаманы сипаттайды.

Бақылау сұрақтары?

1.Тензор деформациясы дегеніміз не?

2.Реологиялық кинематика дегеніміз не?

3.Реологиялық динамика дегеніміз не?

4.Кинематика мен динамиканың айырмашылығы?

ДӘРІС №5 Релаксация кернеуі, тамақ өнімдерінің

сырғығыштығы, тиксотропия

26

Гук моделін кезекпен серпімділік модулі G -мен және Ньютон моделін η тұтқырлықпен қоссақ, релаксацияланған тұтқыр-серпімді Максвелл денесін аламыз. Бұл дененің серпімділігі не тұтқырлық қасиеті уақыт релаксациясының басталуы мен эксперимент өту уақытына тәуелді болып келеді.

Егер серіппені созып, сосын күш түсірсек, онда поршень қозғалысын бастап үлгермейді, сондықтан барлық жүйе Гуктың серпімді денесі болады. Ал егер де пружинаны жібермей созылуды тұрақты сақтаса, онда пружина поршеньді жоғарыға көтеріп, тұрақты тұтқырлықты системаға Ньютонның сұйықтық қасиетін береді.

Максвелл денесінің реологиялық теңдеуін келесідей алуға болады. Максвелл денесінің жалпы деформациясы Гук пен Ньютон денесінің қосындысына тең:

Ньютон денесінің реологиялық теңдеуінен көлемін ( ddtγ н ) анықтаймыз:

Гук денесінің реологиялық теңдеуінің көлемінің ( ddtγ г ) анықталуы:

(1.3 және 1.4) теңдеуіне (1.2) теңдеуін қойып, Максвелл денесінің реологиялық теңдеуін аламыз:

Бірқалыпты деформация (γ = const , ddtγ = 0 ) теңдеуінің шешімі берілген кернеудің уақыт бойынша өзгеруін береді:

27

мұндағы: τ1 - сол уақыттағы кернеу, ол деформациядан кейін бірқалыпты

(1.6) теңдеуі Максвелл денесінің кернеуі бірқалыпты деформация кезінде, уақыт өткен сайын төмендеуін көрсетеді. Бұл құбылыс кернеу

1 - суретінде Максвелл денесінің кернеуінің өзгеру графигі көрсетілген. Бұл графиктен уақыт интервалы 0-ден t1 (γ -const)кернеуіне қарай t → ∞ соңғы бірқалыпты мәнге жеткенше ұмтылып, өсетінін көруге болады.Бірақ, егер t t1 жағдайындағы уақытта деформация жылдамдығы 0-ге тең болады. ( γ = 0,γ = const ), бұл құбылыс 1.6 релаксация кернеу бойынша өзгереді. Енді тұтқыр-серпімді дененің элементтерінің параллель жалғанған кездегі құбылысын қарастырайық. Бұл жағдайда Максвелл моделімен салыстырғанда өзгеше қасиетке ие Кельвин-Фойгтың моделін аламыз. Созылмалы күштің әсерінен серіппе созылып, сұйықтық ішіндегі поршень қозғала бастайды. Поршень қозғалысы сұйықтықтың тұтқырлы қозғалысына байланысты болғандықтан, поршеньнің толық созылуы тез арада болмайды. Күш алынғаннан кейін, пружина өзінің бастапқы ұзындығына тез оралмайды. Оған сұйықтың тұтқырлық кедергісі әсер етеді.

Сонымен, Кельвин-Фойг моделі кешігіп келетін серпімділікпен сипатталады, себебі серпімді Гук денесіне тән. Серпімді деформациясыз тез арада пайда болып және жойылатын қасиеті болуы мүмкін емес.

1 - сурет Максвель денесінің кернеуінің өзгеру диаграммасы Кельвин-Фойг моделінің реологиялық теңдеуін былай аламыз: параллель

жалғанған деформацияның әрбір элементтері өзара тең, сонда

28

мұндағы γ – жалпы деформация.

Бұл кезде күрделі дененің жалпы жанама кернеуі, жеке элементтердің қосындысына тең:

мұндағы τг және τн - Гук пен Ньютон денелеріне сәйкес қатысты дене.

1.8 теңдеуінің оң жағына Ньютон мен Гук денесінің реологиялық теңдеуінің τг және τн мәндерін қойсақ, бұл түрлендіруден кейінгі КельвинФойг денесінің реологиялық теңдеуін аламыз.

Кернеуді τ =const деп ала отырып, (1.9) теңдеуінен мына теңдікті аламыз:

жетпей кешігіп жететінін көреміз. Кешігіп жету уақытының теңдеуі былай анықталады:

λ = ηG

(1.11)

Егер t1 уақытында кернеуді алып тастасақ, деформация жылдам жоғалып кетпейді, керісінше, ақырындап бірқалыпты мәнге жеткенше төмендеуін көруге болады. Бұл байланыс:

(1.12)

(1.12) теңдеуінің қорытындысы t → ∞ деформация 0-ге ұмтылғанда кез келген соңғы уақытта материалда қалдық деформацияның болатындығын көрсетеді.

29

2- сурет Кельвин-Фойгт денесінің кернеуінің өзгеру диаграммасы

төмендейді.

Реалды тағам материалдары жылдам серпімділікке, кешігіп келетін серпімділікке және қалдықты деформация қасиетіне ие. Бұндай материалдарға мысал ретінде, қамырды, конфеттік массаны және т.б тағамдық материалдарды жатқызуға болады. Бұл модельдер тізбектеліп байланысқан 2 немесе одан да көп модельдерден тұрады.

Реалды материалдардың бірқалыпты кернеуінде, уақыт бойынша деформациясын арттыру сырғанағыштық деп аталады. Ал графиктегі уақытқа тәуелді деформация сырғығыштық деп аталады.

Кернеуді τ тез арада t =0 жағдайында қойса, серпімді жылдам аралық деформация γ1 = τ / G1 пайда болады. Ары қарай деформация қисық АВ сызығымен жалғасады.

3- сурет

Бұл бөлікте бір мезгілде кешігіп келетін серпімді деформация

30