Типовой вариант контрольной работы №1 (тема «Дифференциальное исчисление функции одной переменной»)

1. Найдите пределы: а) 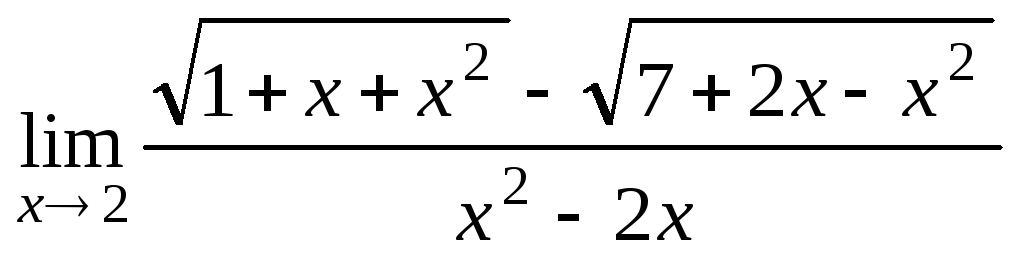;б) .

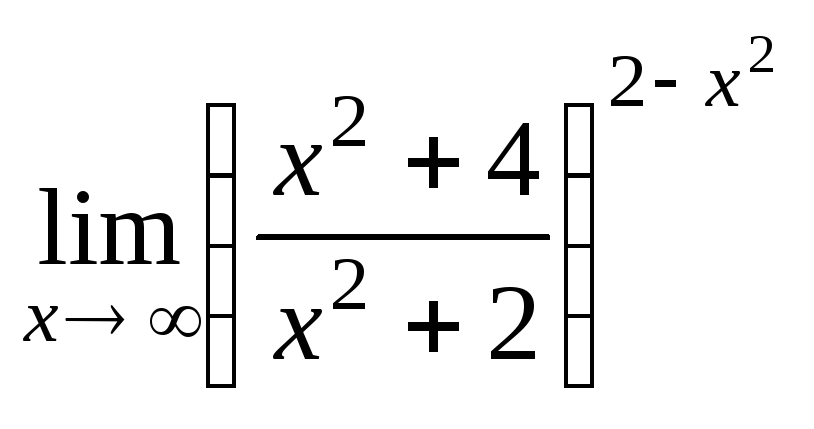2. Найдите производную : а) ; б) ;

в) .

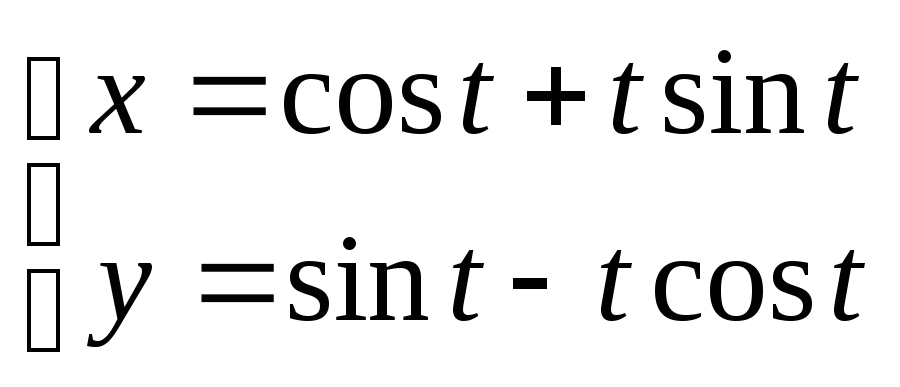3. Исследуйте на экстремум функцию:

4. Найти экстремум функциипри условии.

Решить задачу с помощью введения функции Лагранжа. Изобразить:

• график условия,

• изолинии, проходящие через стационарные точки функции Лагранжа,

• градиент в этих точках.

5. Спроси предложениезависят от ценыследующим образом:,. Найти наибольшее значение дохода и определить эластичность функции дохода в точке максимума.

Дополнительные задания (засчитываются при условии, что в первой части было набрано шесть баллов)

1. Доказать, что градиент функции в точкеи изолиния, проходящая через эту точку, ортогональны.

2. Доказать монотонность последовательности .

3. Найдите значения AиB, при которых функцияявляется бесконечно малой :

.

Типовой вариант контрольной работы № 2 (тема «Интегральное исчисление функции одной переменной»)

1. Найдите интегралы:

;	;	;
;	;

2. Исследовать ряды на сходимость:

3. Исследовать на сходимость интеграл .

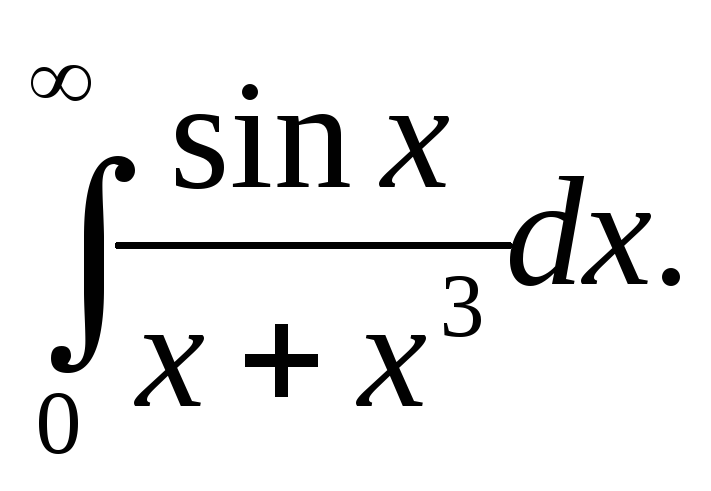4. Найти производную функции

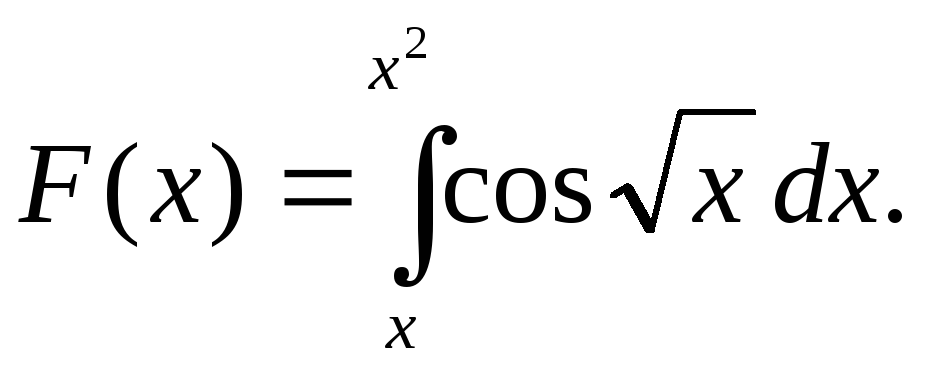
Типовой вариант контрольной работы № 3 (тема «Линейная алгебра и аналитическая геометрия»)

1. Решить систему алгебраических линейных уравнений по правилу Крамера, матричным способом и методом Гаусса:

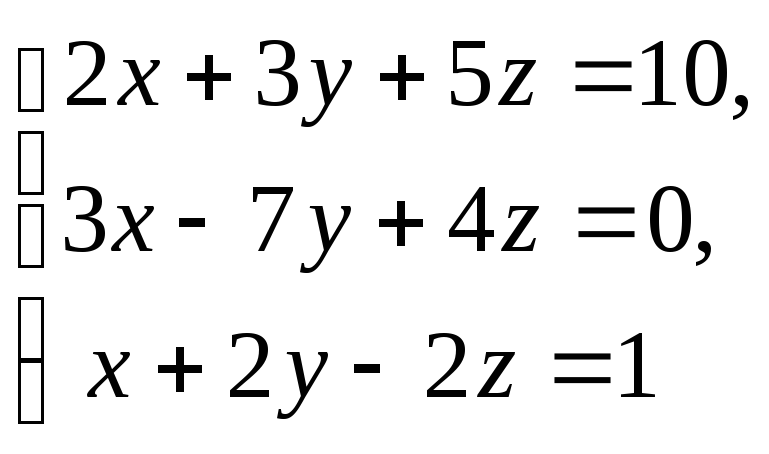
2. Даны координаты точек: .

Найти:

1. Координаты векторов 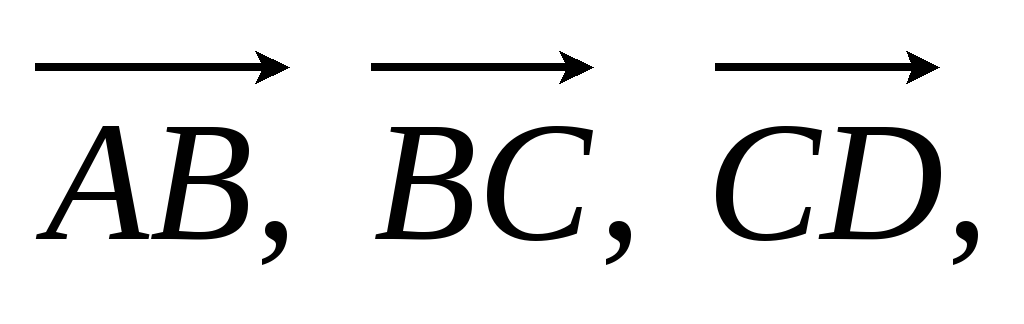и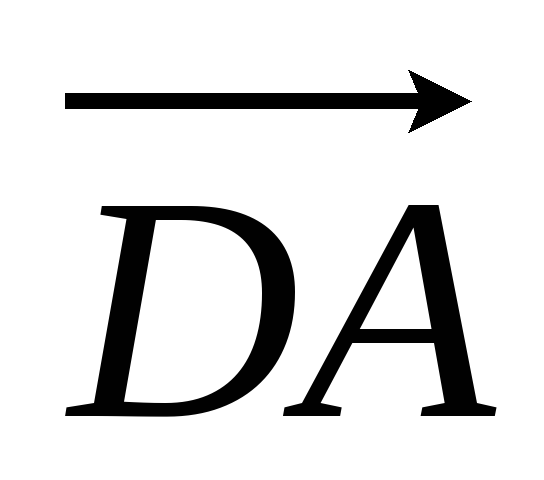, записать их разложение по базису.

2. Координаты вектора .

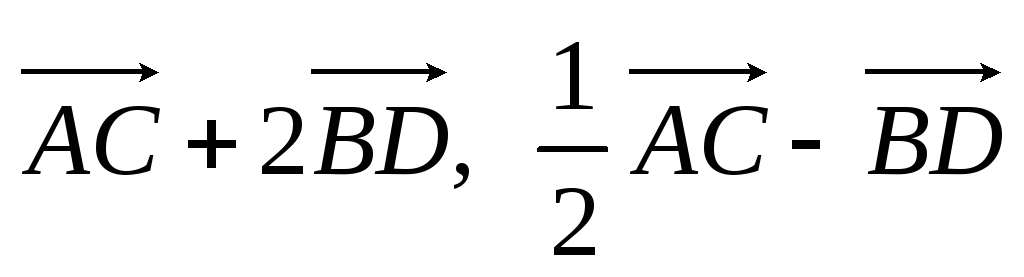3. Периметр треугольника .

4. Косинус внутреннего угла .

5. Площадь треугольника .

6. Длину высоты треугольника 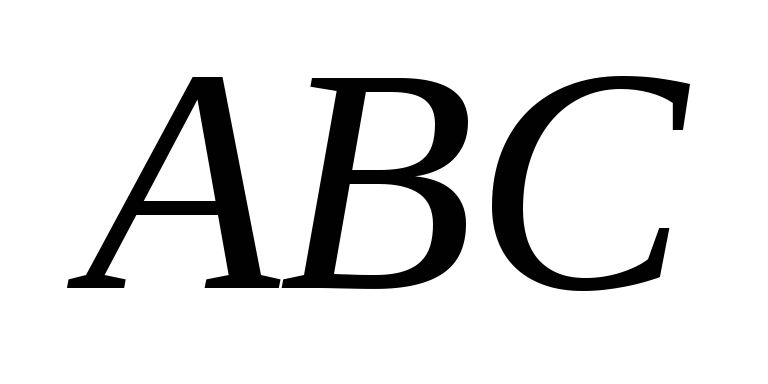, лежащего в основании пирамиды, опущенную из вершинына сторону.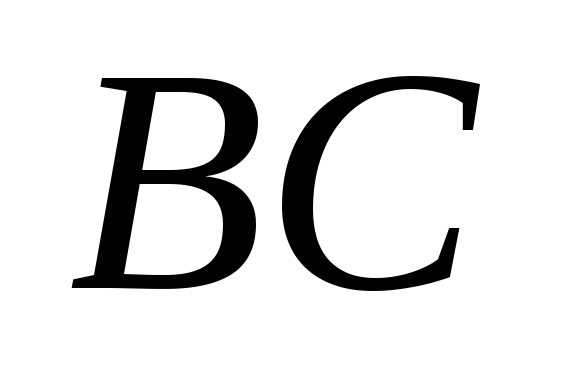

3. Даны вершины треугольника А(-1; 2);В(7; -2);С(3; -5). Составить уравнения:

1) Медианы, проведенной из вершины А.

2) Высоты, проведенной из вершины В.

3) Уравнение прямой, проходящей через вершину Впараллельно сторонеАС.

Типовой вариант контрольной работы № 4 (тема «Теория вероятностей и элементы математической статистики»)

1. На четвертом курсе одного из факультетов читается шесть спецкурсов. Каждый четверокурсник обязан выбрать для посещения два спецкурса. Сколькими способами он может это сделать?

2. Среди 100 изделий 20 бракованных. Найти вероятность того, что среди шести наугад взятых изделий будет четыре бракованных.

3. В магазин поступила партия из 20 пар мужских туфель и 25 пар женских. В среднем 12 % мужских туфель и 6 % женских имеют различные дефекты отделки. Наугад выбрали одну пару, которая оказалась с дефектами отделки. Какова вероятность того, что это мужские туфли.

4. В среднем 10 % автомобилей, производимых заводом, имеют брак. Для контроля из партии автомобилей взяли пять машин. Найти вероятность того, что среди них будет: а) три машины без брака; б) не более трех машин без брака.

5. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка разобьется, равна 0,03. Найти вероятность того, что магазин получит разбитых бутылок: а) ровно две; б) более двух.

6. В среднем 7 % книг, выпускаемых типографией, имеют мелкие полиграфические дефекты. Найти вероятность того, что в партии из 400 книг дефекты будут иметь: а) 28 книг; б) от 34 до 45 книг; в) не менее 52 книг.

7. Плотность распределения вероятностей НВС Химеет вид:

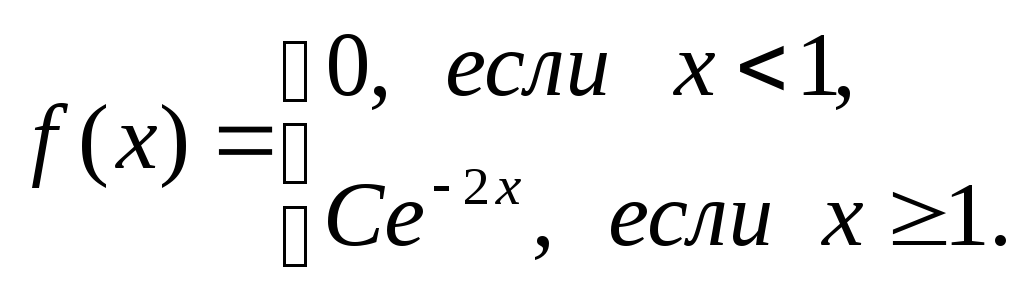
Найти: а) константу С; б) Р(|Х|2); в) функцию распределенияF(х).

Дополнительные задания (засчитываются при условии, что в первой части было набрано пять баллов)

1. Функция распределения НВС Химеет вид:

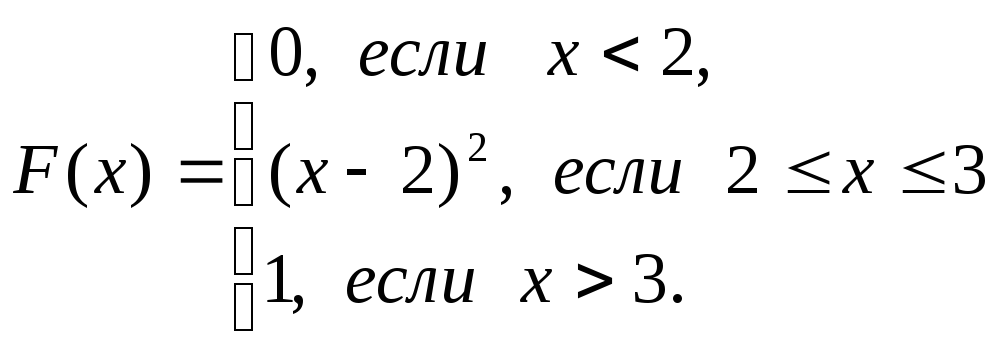
Найти: а) Р(0,5Х2,5); б)M[X]; в)D[X].

2. Автобусы идут с интервалом в пять минут. Считая, что случайная величина Х– время ожидания автобуса на остановке – распределена равномерно на указанном интервале, найти среднее время ожидания и дисперсию времени ожидания.

3. Время ожидания у бензоколонки АЗС является случайной величиной Х, распределенной по показательному закону со средним временем ожидания, равным шести минутам.

Найти: а) Р(3Х<9); б) Р(Х12).

4. Длина детали, изготавливаемой на автоматическом станке, является случайной величиной, распределенной по нормальному закону с параметрами m = 20,= 0,2. Найти вероятность того, что длина детали будет находиться в интервале (19,7; 20,3). Какую точность изготовления можно гарантировать с вероятностью 0,9?