2.7 Практические занятия № 13 – 15. Алгебры с двумя бинарными операциями. Кольца. Поля. Решетки. Булевы алгебры

2.7.1 Теоретические сведения и методические рекомендации по решению задач

Алгебра называетсякольцом, если выполняются следующие условия:

1) – абелева группа;

2) ­– полугруппа;

3) операция дистрибутивна справа и слева относительно операции.

Кольцо называетсякоммутативным, если–коммутативная операция.

Если в кольце есть единица, т.е., тоназываетсякольцом с единицей.

Алгебра называетсяполем, если выполняются следующие условия:

1) –абелева группа;

2) –абелева группа, в которой обратим каждый ненулевой элемент;

3) операция дистрибутивна относительно операции.

2.7.2 Примеры решения задач

Задача 1. Доказать, что все обратимые элементы кольца <К, +, ∙> с единицей образуют группу относительно умножения.

Решение.Умножение во множестве К ассоциативно, единица содержится во множестве обратимых элементов (в самом деле, единица себе обратна), и произведение не выводит из множества обратимых элементов, так как если элементыaиbобратимы то. Тем самым, в кольце для обратимых элементов выполняются все аксиомы группы относительно умножения.

Задача 2. Доказать, что алгебра, называемая двоичной арифметикой, является полем. Здесь- сложение по модулю 2 и· - конъюнкция.

Решение. Очевидно, что сложение по модулю 2 и конъюнкция замыкают бинарное множество {0, 1}.

В курсе математической логики доказано, что конъюнкция и сложение по модулю 2 – коммутативные, ассоциативные операции, эти факты подтверждаются следующими равносильными формулами алгебры логики:

;

;

;

.

Также ранее было доказано, что конъюнкция дистрибутивна относительно сложения по модулю 2, т.е.

.

Нейтральным элементом относительно операции является 0. В самом деле,. Аналогично, нейтральным элементом для операции конъюнкция является 1, так как.

Найдем симметричные для 0 и 1 элементы относительно операции и симметричный 1 элемент относительно операции конъюнкция:

, так как;

, так как;

, так как.

Обратим внимание на то, что симметричный 0 элемент относительно операции конъюнкция искать не нужно, так как 0 является нейтральным элементом относительно операции .

Таким образом, все аксиомы поля выполняются, а алгебра образует поле.

2.7.3 Задачи для самостоятельного решения

1. Доказать, что матрицы вида 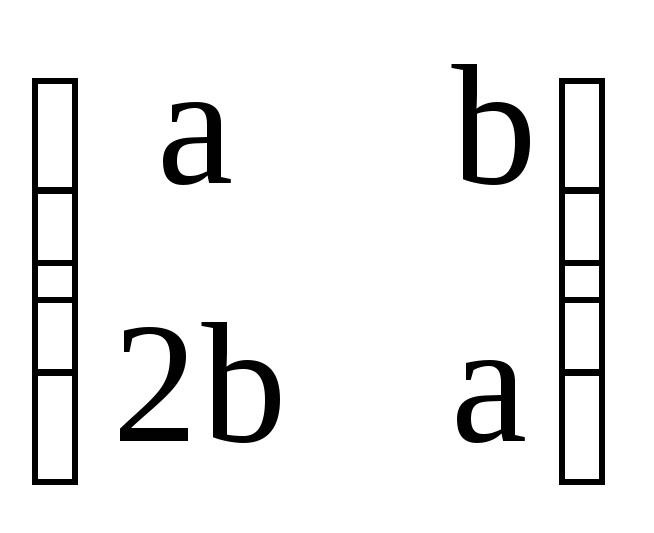с действительными коэффициентамиa, bобразуют кольцо относительно операций «сложение» и «умножение» матриц.

2. Образует ли поле относительно операций «сложение» и «умножение» множество матриц вида :

а) с рациональными коэффициентами;

б) с действительными коэффициентами?

3. Образует ли булеан коммутативное кольцо относительно операций «объединение» и «пересечение» множеств?

4. Образует ли булеан поле относительно операций «симметрическая разность» и «пересечение» множеств?

5. Образуют ли поле относительно операций сложения и умножения комплексные числа a+bi:

а) с целыми а иb;

б) с рациональными а иb;

в) с действительными а иb?

6. Образует ли множество {a, b} поле относительно операций * и, заданных таблицами Кэли:

*	a	b
a	a	b
b	b	a

	a	b
a	a	a
b	a	b

7. Пусть –множество простых чисел, не превосходящихp, а- множество произведений различных чисел из. Доказать, что <P; НОД, НОК, ДОП>–булева алгебра, где НОД – наибольший общий делитель, НОК – наименьшее общее кратное, ДОП(n)=.

8. Проиллюстрировать изоморфизм между булевыми алгебрами множеств и логических функцийдля.

9. Выполнить булевы операции над логическими функциями трех переменных f₁ и f₂, используя изоморфизм булевых алгебр логических функций и двоичных векторов, если:

а) f₁ и f₂ определены таблицами истинности

xyz	f1	f2
000	0	0
001	0	0
010	0	1
011	1	1
100	1	0
101	0	1
110	1	1
111	1	1

б) f₁ и f₂ определены своими СДНФ:,.