Дифференциальные уравнения второго порядка Уравнения допускающие понижение порядка

1. Уравнение вида

Это уравнение не содержит в явном виде искомой функции у(х). Сделаем замену Тогда

2. Уравнение вида

Это уравнение не содержит в явном виде аргумент х, поэтому для его решения предлагается замена т.е.z является функцией от у, а не от х.

Тогда

Итак,

Пример 6. Решить уравнение

Решение:

1)

линейное однородное уравнение первого порядка, решение которого

2) уравнение с разделяющимися переменными.

Линейным однородным дифференциальным уравнением второго порядканазывается уравнение вида

для нахождения линейно независимых решений иуравнениянадо записать по линейному однородному дифференциальному уравнению второго порядка характеристическое уравнение:

и решить его, т.е. найти корни и.

Возможны три случая

1. Корни ихарактеристического уравнения вещественные и различные,т.е.тогда общее решение дифференциального уравнения имеет вид:

2. Корни ихарактеристического уравнения вещественные и равные друг другут.е.тогда общее решение дифференциального уравнения имеет вид:

3. Корни ихарактеристического уравнения комплексно–сопряжённыет.е.гдетогда общее решение дифференциального уравнения имеет вид:

Пример 7. Решить уравнение:

Решение:

Составим и решим характеристическое уравнение:

Мы получили действительные и различные корни, следовательно, общее решение данного уравнения находим по формуле:

Получим:

Задания для самостоятельного решения

1.Решить уравнение:

а)

б)

2.Найдите частное решение данного уравнения

а)

б)

3. Решить уравнение:

а)

б)

в)

г)

д)

4. Решить уравнение:

1)

2)

3)

5. Найдите частное решение уравнения удовлетворяющее начальным условиям

6. Решить уравнение:

1)

2)

3)

4)

Рекомендуемая литература: 1.1, 1.2, 2.2.

Самостоятельная работа №11

Тема: «Разложение функций в степенные ряды»

Цель: Закрепление умения использования формул Тейлора и Маклорена для разложения функций в степенные ряды.

Время выполнения: 6 часов

Теоретические сведения

Числовым рядом называется бесконечная последовательность чисел , соединенных знаком сложения:

Числа называютсячленами ряда, а член -общим или n-м членом ряда.

Среди рядов особое место занимают степенные ряды, членами которых являются степенные функции аргумента х:

Действительные числаназываются коэффициентами ряда,х – действительная переменная.

Рассмотренный степенной ряд расположен по степеням х.

Имеют место ряды, расположенные по степеням , т.е. ряд вида

,

где - некоторое постоянное число.

Для приложений важно уметь данную функцию f(x) разлагать в степенной ряд, т. е. функцию f(x) представлять в виде суммы степенного ряда.

Для любой функции f(x), определённой в окрестности точки и имеющей в ней производные до(n+1)-го порядка включительно, справедлива формула Тейлора:

где ,- остаточный член в форме Лагранжа.

Число с можно записать в виде , где.

Без остаточного члена имеем – многочлен Тейлора:

.

Если функция f(x) имеет производные любых порядков (т. е. бесконечно дифференцируема) в окрестности точки и остаточный членстремится к нулю при, то из формулы Тейлора получается разложение функцииf(x) по степеням , называемое рядом Тейлора:

.

Если в ряде Тейлора положить , то получим разложение функции по степенямx в так называемый ряд Маклорена:

.

Формально ряд Тейлора можно построить для любой бесконечно дифференцируемой функции (это необходимое условие) в окрестности точки . Но отсюда ещё не следует, что он будет сходиться к данной функции f(x); он может оказаться расходящимся или сходиться, но не к функцииf(x).

Пример1. Разложить многочлен

в ряд Тейлора при

Решение:

Найдём производные данного многочлена:

В точке имеем:

По формуле

получаем:

Пример 2. Записать формулу Тейлора и выражение остаточного члена для

при n = 4 и

Решение:

Формула Тейлора имеет вид:

где

Найдём производные функциив точке

Искомая формула имеет вид:

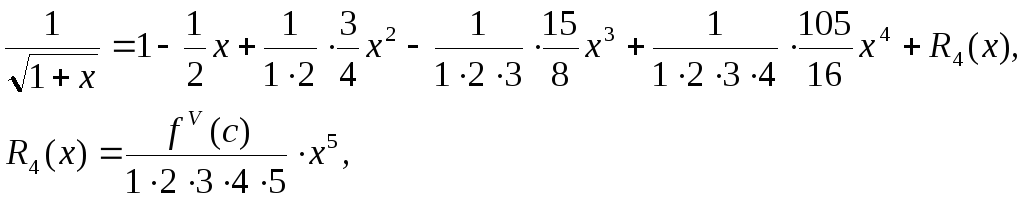
где и, т.е.

.

Для того чтобы ряд Тейлора функции f(x)

сходился к f(x) в точке x, необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора стремился к нулю при , т. е..