Задания для самостоятельной работы

1. Вычислите скалярное произведение векторов:

2. Ортогональны ли векторы:

3. Найдите угол между векторами:

Рекомендуемая литература: 1.1, 2.1,2.5.

Самостоятельная работа №4

Тема: «Кривые второго порядка»

Цель: Формирование умения составления уравнений кривых второго порядка

Время выполнения: 4 часа

Теоретические сведения

Если Р(х; у) многочлен второй степени, то линии, определяемые уравнением

Р(х; у)=0 (1),

называются линиями второго порядка, а уравнение (1) может быть записано в виде

Линия второго порядка, задаваемая уравнением (2) в зависимости от коэффициентов А, В, С, D, Е, F, определяет эллипс, гиперболу или параболу, а при некоторых значениях коэффициентов - точку или две прямые (последние случаи называют вырожденными).

Окружность

Окружностью радиуса R с центром в точке называется множество всех точек М плоскости, удовлетворяющих условию(см. рис.1).

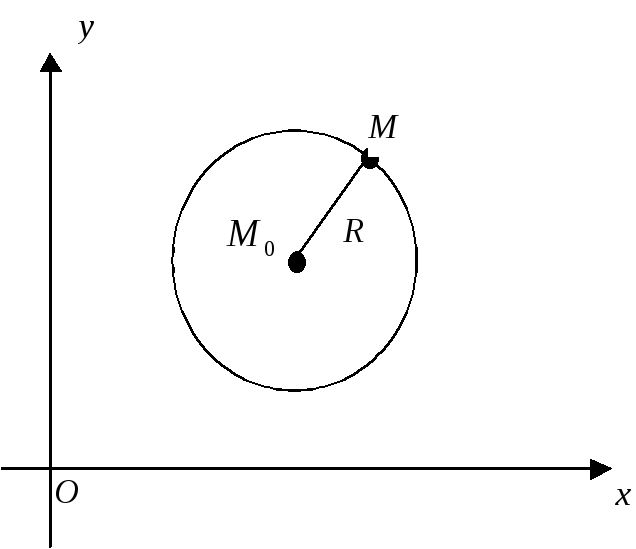
Рис.1.

Каноническое уравнение окружности имеет вид:

где х, у – текущие координаты,

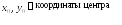
R – радиус окружности.

В частности, полагая получим уравнение у первого коэффициенты приодинаковы и отсутствует окружности с центром в начале координат

Как было сказано выше, окружность является линией второго порядка, следовательно, её уравнение тоже можно рассматривать как частный случай уравнения (2).

Если мы раскроем скобки в уравнении (3), то после некоторых преобразований мы получим уравнение вида

Мы видим, что уравнение (4) отличается от уравнения (2) только тем, что член, содержащий произведение ху.

Таким образом, окружность определяется общим уравнением второй степени с двумя переменными, если в нём коэффициенты при равны между собой и отсутствует член с произведениемху.

Эллипс

Эллипсом называется множество точек плоскости, декартовы координаты, которых удовлетворяют уравнению:

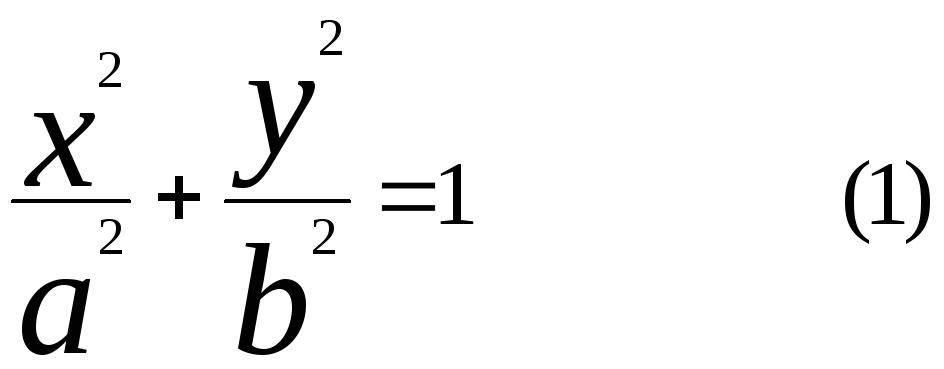
Числа а и b - полуоси эллипса.

Эллипс - это линия симметричная относительно осей Ох и Оу.

Точки

называются вершинами эллипса.

Из канонического уравнения эллипса мы можем вывести формулы для вычисления х и у:

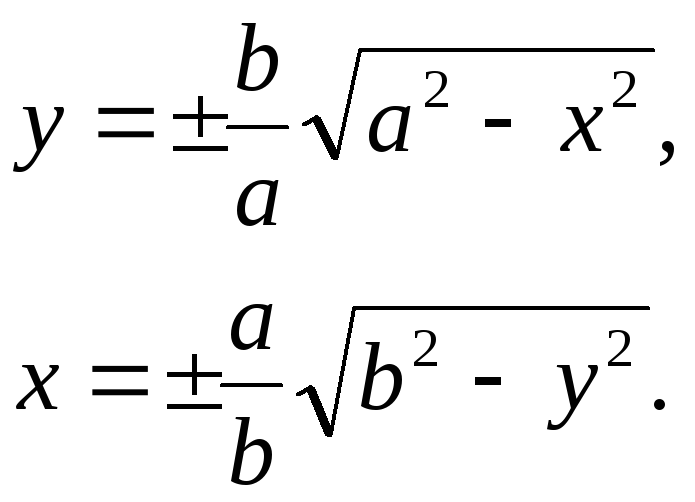
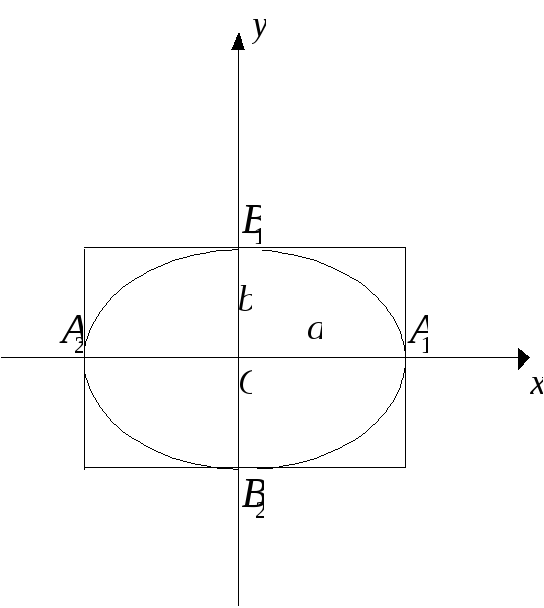
Рис.1.

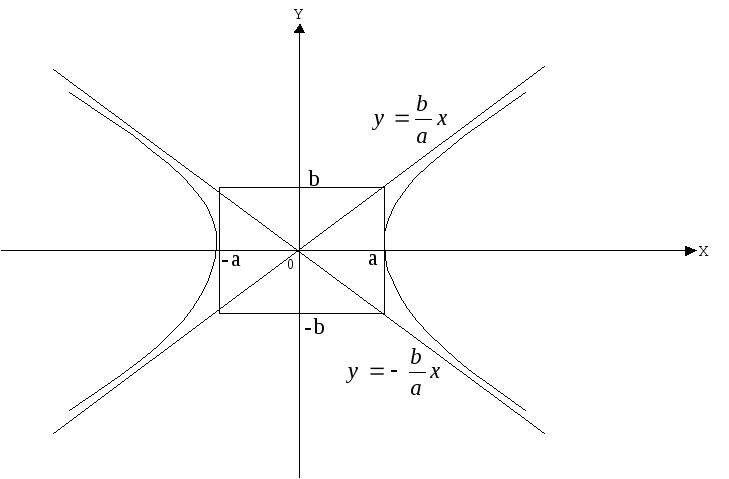
Гипербола

Гиперболой называется множество точек плоскости, декартовы координаты, которых удовлетворяют уравнению:

Из канонического уравнения гиперболы выводим уравнения х и у:

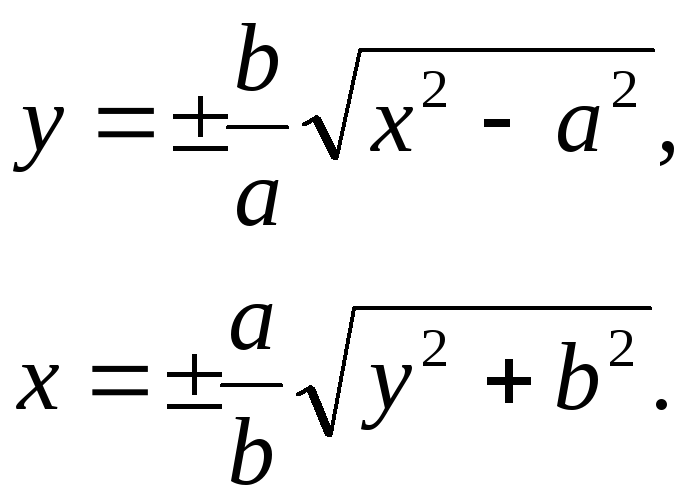
Гипербола состоит из двух частей, называемых ветвями.

При a=b гипербола называется равносторонней (равнобочной) и её уравнение имеет вид

Гипербола, заданная уравнением вида имеет вид:

Гипербола, заданная уравнением вида называетсясопряжённой гиперболе .

Центром гиперболы является начало координат. Точки пересечения гиперболы с осями симметрии называются вершинами гиперболы.

Числа a ,b –полуосями.

Прямые

являются асимптотами гиперболы.

Задание для самостоятельной работы

Номер задачи	Текст задачи
1	Составить уравнение гиперболы с фокусамина оси Ох, если расстояние между ее фокусами равно 20, а уравнение ее асимптот . Составить уравнение директрисы параболы у2-4у-12х+16=0.
2	Составить уравнение эллипса с фокусами на оси Ох, если расстояние между фокусами равно16, а эксцентриситет равен ½. Составить уравнение оси параболы у2-6у-12х-15=0.
3	Составить уравнение эллипса с фокусами на оси Ох, если расстояние между фокусами равно12, а эксцентриситет равен 3/10. Составить уравнение оси параболы у2+6у-8х+1=0.
4	Составить уравнение эллипса с фокусами на оси Ох, проходящего через точки А(6;4) и В(). Составить уравнение директрисы параболы у2+8у+28х+72=0.
5	Составить уравнение эллипса с фокусами на оси Ох, проходящего через точки () и (). Составить уравнение оси параболы у2-4у-16х+52=0.
6	Найти эксцентриситет эллипса . Составить уравнение оси параболы Х 2 +8х+16у+48=0.
7	Найти эксцентриситет гиперболы . Составить уравнение директрисы параболы Х 2 +8х-28у+44=0.
8	Дан эллипс . Найти его полуоси и расстояние между фокусами. Написать уравнение гиперболы, проходящей через точку (2;1) , асимптоты которой .
9	Дана гипербола . Найти ее оси и расстояние между фокусами. Написать уравнение параболы с вершиной в начале координат, если координаты фокуса равны F(0;-5).
10	Найти эксцентриситет эллипса 4х2+9у2=180. Написать уравнение директрисы и найти координаты фокуса параболы У2=4х.

Рекомендуемая литература: 1.1, 2.1.