2.1. Запись уравнения теплопроводности для ограниченного стержня. Формулировка задачи.

В качестве дальнейшего примера возьмем задачу о распространении тепла в ограниченном стержне. Стержень представляет собой одномерное пространственное тело (т.е. его радиус не учитывается) расположенное вдоль координаты (см. рисунок 2). Температура стержня в каждой точке будет определяться сложной функцией зависящей от координатыи времени- .

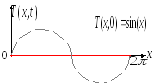
Рисунок 2. Задача распространение тепла в стержне

Рассмотрим задачу распространения тепла в стержне, предполагая, что тепловыделение отсутствует (нет внутренних источников). В этом случае процесс теплопередачи будет описываться уравнением теплопроводности для частного случая (10) и одной координаты:

или

Примем следующие допущения: значение коэффициента ; стержень ограничен с двух сторон – в точке и.Получим следующую запись уравнения с учетом ограничений:

, ,(данное ограничение говорит о том, что мы не рассматриваем процессы до начала моделирования)

Для того чтобы сформулировать задачу, необходимо дополнить уравнение начальными и краевыми условиями.

Начальные условия – пусть в начальный момент времени () стержень нагрет так, что профиль его температуры по координате представляет собой синусоиду, т.е. при(см. рисунок 2).

Краевые условия – пусть на концах стержня (, ) температура не изменяется с течением времени, т.е. ипри

Таким образом, постановка задачи для данного примера означает нахождение функции удовлетворяющей следующим условиям:

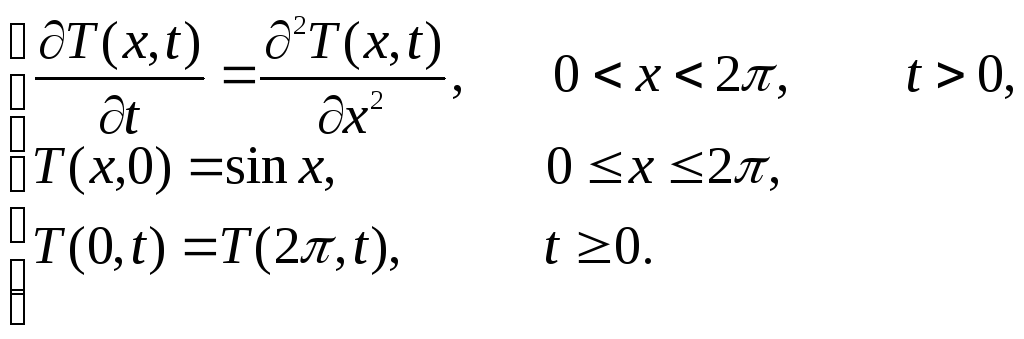
2.3 Решение задачи распространения тепла в ограниченном стержне. Метод разделения Фурье.

Решение задачи означает нахождение конкретного вида (частного) функции -частного решения исходного дифференциального уравнения.

Для решения поставленной задачи воспользуемся методом разделения Фурье. Алгоритм решения по этому методу для данного примера следующий:

• представление функции 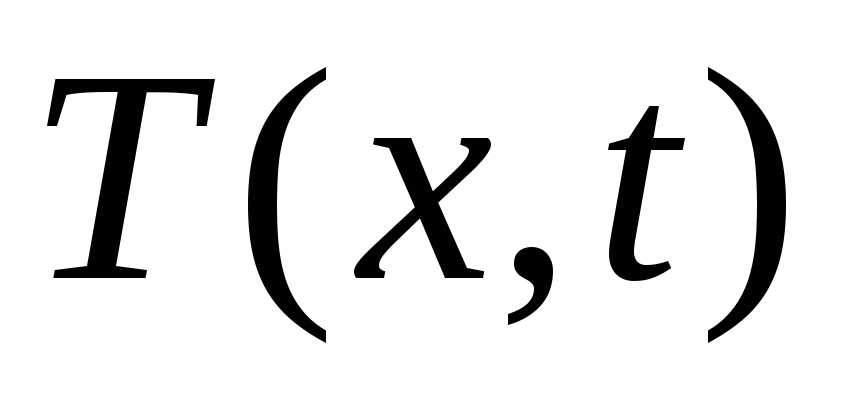как совокупности функций в раздельных переменных

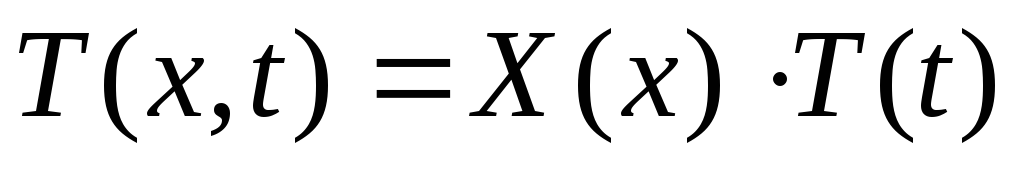
• нахождение решений функци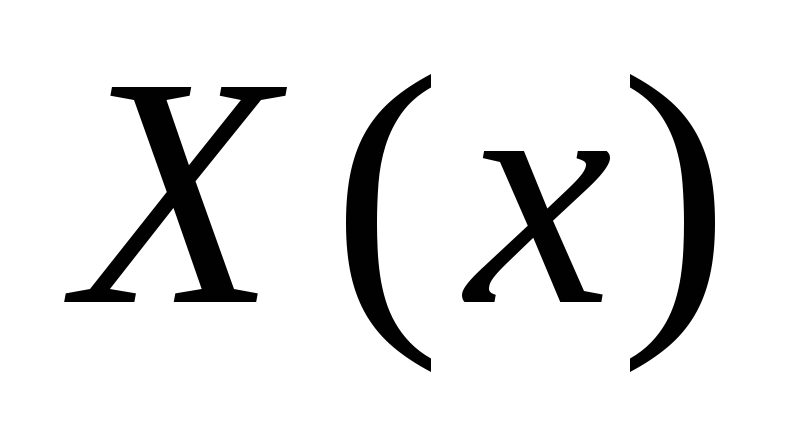й и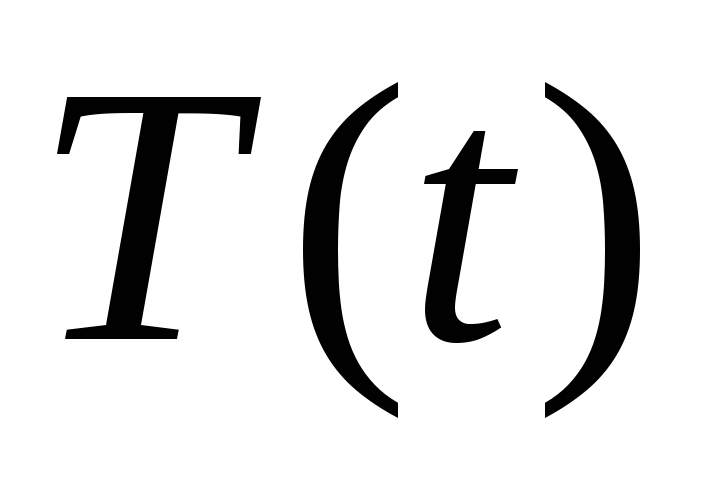раздельно

• объединение решений функци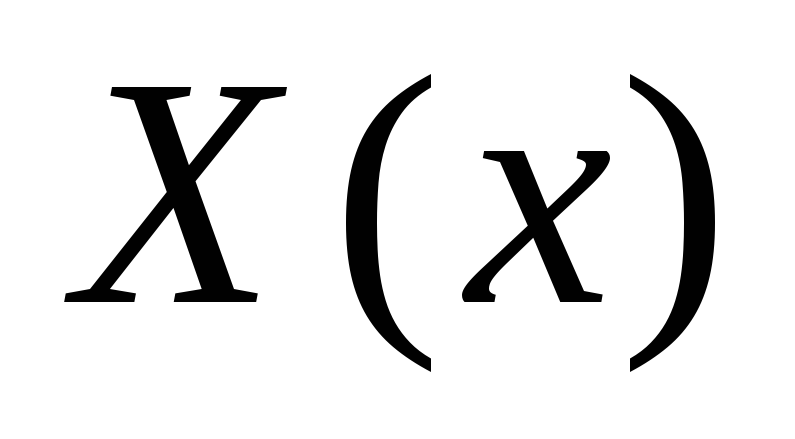й и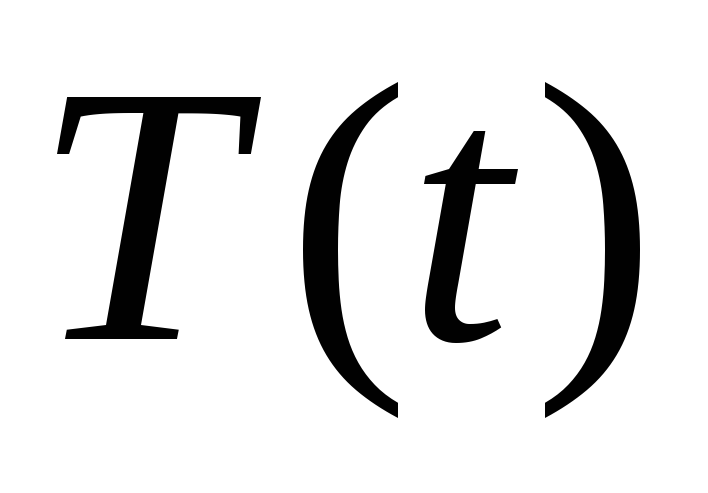

• нахождение искомого частного решения исходной функции

2.3.1 Преобразование исходной функции

Преобразуем функцию и подставим ее в исходное уравнение:

Поскольку под знаком производной стоят функции от одного аргумента (по которому и берется производная), то частные производные обратятся в обыкновенные:

Это уравнение в разделенных переменных, которое можно записать в виде:

или в кратком виде

Так как правая и левая части этого уравнения зависят от разных переменных, то они равны только в том случае, если являются константой, т.е. при:

что равносильно записи и

2.3.2 Поиск решений функции

Будем искать решение уравнения , для чего примеми отсюда:

Получим обыкновенное линейное однородное дифференциальное уравнение. Для его решения необходимы краевые условия, которые наследуются из краевых условий исходной задачи:

и

В итоге пришли к тому, что нам необходимо решить систему:

Данная система представляет собой т.н. задачу Штурма-Лиувилля, связанную с нахождением общего решения дифференциального уравнения системы с учетом всех возможных значений параметра .

Можно показать, что общее решение данного уравнения запишется в виде:

где - константа. Среди всего множества значенийнетривиальному решению (отличному от нуля) выбираются только удовлетворяющие следующему условию:

где . Т.е. от бесконечного множества решений переходим к бесконечному счетному множеству вида:

зависящему от (в т.ч. с константой различной для разных)

2.3.2 Поиск решений функции

Будем искать решение уравнения

Получим обыкновенное линейное однородное дифференциальное уравнение. Поскольку значения параметра уже получены, то искомое решение данного уравнения сразу можно записать в виде:

где - константа.

2.3.3 Объединение решений

Подставляя полученные решения в формулу получим следующую запись:

Данное уравнение отражает множественность общих решений дифференциального уравнения в частных производных. Доказано, что линейная комбинация общих решений также является общим решением, поэтому «наиболее полное» общее решение исходной задачи представляется зависимостью в виде ряда:

2.3.4 Нахождение частного решения

Для нахождения частного решения (а с ним и решения задачи) необходимо воспользоваться начальным условием :

Для любых нет значений коэффициентовприводящих данное выражение в верное тождество. Соответственно только приуравнение имеет искомое решение, при этом коэффициентопределиться следующим образом:

,

а остальные коэффициенты будут равны нулю: ,.

Итоговое частное решение уравнения (задачи) запишется так:

Для проверки найденного решения его необходимо подставить в исходное уравнение:

получаем верное тождество.