
- •«Системи та методи прийняття рішень»
- •Перелік практичних занять практичне заняття 1
- •Короткі теоретичні відомості
- •1 Постановка задачі прийняття рішень
- •2 Приклади задач прийняття рішень
- •3 Класифікація задач прийняття рішень
- •Розв’язування задач
- •1.3 Контрольні питання
- •2.2 Розв’язування задач
- •2.3 Контрольні питання
- •3.2 Розв’язування задач
- •Контрольні питання
- •Література: [2, 119-123; 4, 40-45]. Практичне заняття 4
- •4.1 Короткі теоретичні відомості
- •1 Розв’язання задач багатокритеріальної оптимізації
- •2 Принцип головного критерію
- •3 Функціонально-вартісний аналіз
- •4 Принцип послідовної оптимізації ( лексикографічного впорядкування)
- •4.2 Контрольні питання
- •2 Вимірювання та шкалування частинних критеріїв
- •3 Формування функції корисності частинних критеріїв
- •4 Перетворення дихотомічного якісного фактора
- •5 Перетворення багатозначного якісного фактора
- •5.2 Контрольні питання
- •2 Універсальна математична модель багатокритеріального оцінювання й оптимізації
- •3 Реалізація адитивної оцінки
- •4 Реалізація моделі послідовної оптимізації
- •5 Реалізація мінімаксної та максимінної оцінок
- •6.2 Розв’язування задач
- •6.3 Контрольні питання
- •Література: [14, 119-123; 17, 140-145].
- •7.1.2 Аналіз рішень в екстенсивній (узагальненій) формі
- •7.1.3 Аналіз рішень у нормальній формі
- •7.1.2 Критерії прийняття рішень в умовах стохастичної невизначеності
- •7.2 Розв’язування задач
- •7.3 Контрольні питання
- •8.2 Розв’язування задач
- •8.3 Контрольні питання
- •Література: [14, 119-123; 17, 140-145]. Практичне заняття 9
- •9.2 Розв’язування задач.
- •9.2 Розв'язування задач
- •9.3 Контрольні питання
- •Практичне заняття 10
- •10.2 Розв’язування задач.
- •10.1 Короткі теоретичні відомості
- •3 Критерій мінімаксного ризику Севіджа
- •10.2 Розв’язування задач
- •10.3 Контрольні питання
- •11.2 Розв’язування задач
- •11.3 Контрольні питання
- •Принцип оптимальности Беллмана
- •Задача о наборе высоты и скорости летательного аппарата.
- •Функциональное уравнение Беллмана.
- •Задача распределения ресурсов.
- •Распределение по неоднородным этапам.
- •Распределение ресурсов между тремя и более отраслями.
- •Распределение ресурсов с резервированием.
- •Распределение ресурсов «с вложением доходов в производство».
- •Учёт предыстории процесса.
- •Задача с мультипликативным критерием.
- •Література: [14, 119-123; 17, 140-145].
- •13.2 Розв’язування задач.
- •4.11. Применение метода динамического программирования для решения задачи управления запасами
- •13.3 Контрольні питання Література: [8, 119-123; 17, 140-145]. Список літератури
- •39614,М.Кременчук, вул. Першотравнева, 20
2.2 Розв’язування задач
Приклад 2.1 Нехай функція корисності особи, що не схильна до ризику зображена на рис. 2.3.
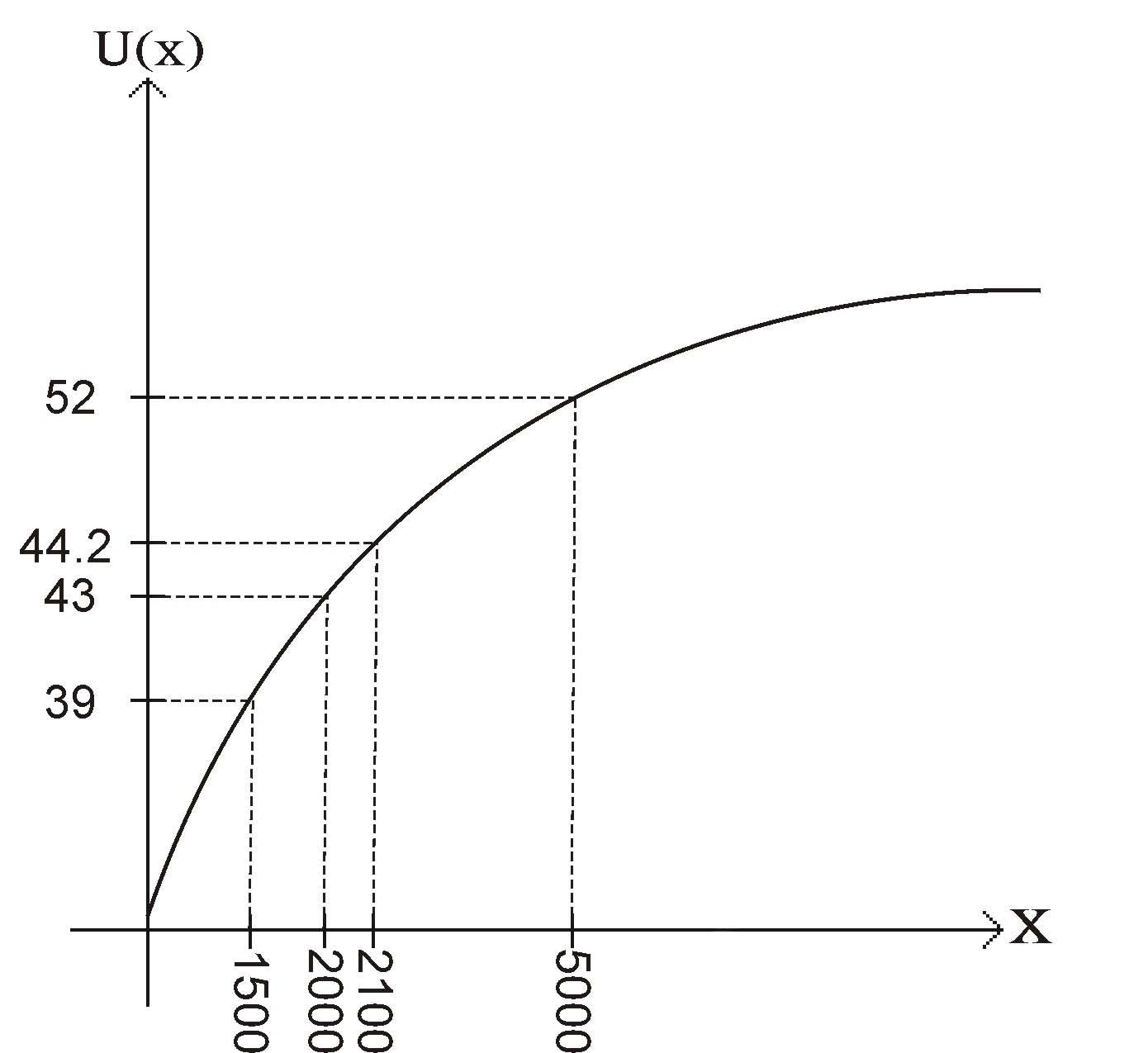
Рисунок 2.3
У лінії прийняття рішень має 2 альтернативи: або мати постійний дохід 2000 грн., або погодитись на нову роботу, де він зможе отримати 5000 грн. з ймовірністю 0,4. Або 1500 грн. з ймовірністю 0,6.
Яке рішення потрібно прийняти?
Розв’язання: За формулою (2.2) знаходимо корисність:
![]()
Відповідне
значення корисності роботи, на якій він
зараз знаходиться
![]() .
.
Так
як корисність отриманої функції більше,
тобто
![]() ,
тому краще змінити роботу.
,
тому краще змінити роботу.
Знайдемо
детермінований еквівалент
![]() ,
,![]() .
.
За формулою (2.1):
![]()
![]()
Відповідь. Роботу краще буде змінити, премія за ризик буде складати 800 грн.
Приклад 2.2 Особа яка схильна до ризику має функцію корисності зображену на рис. 2.4.
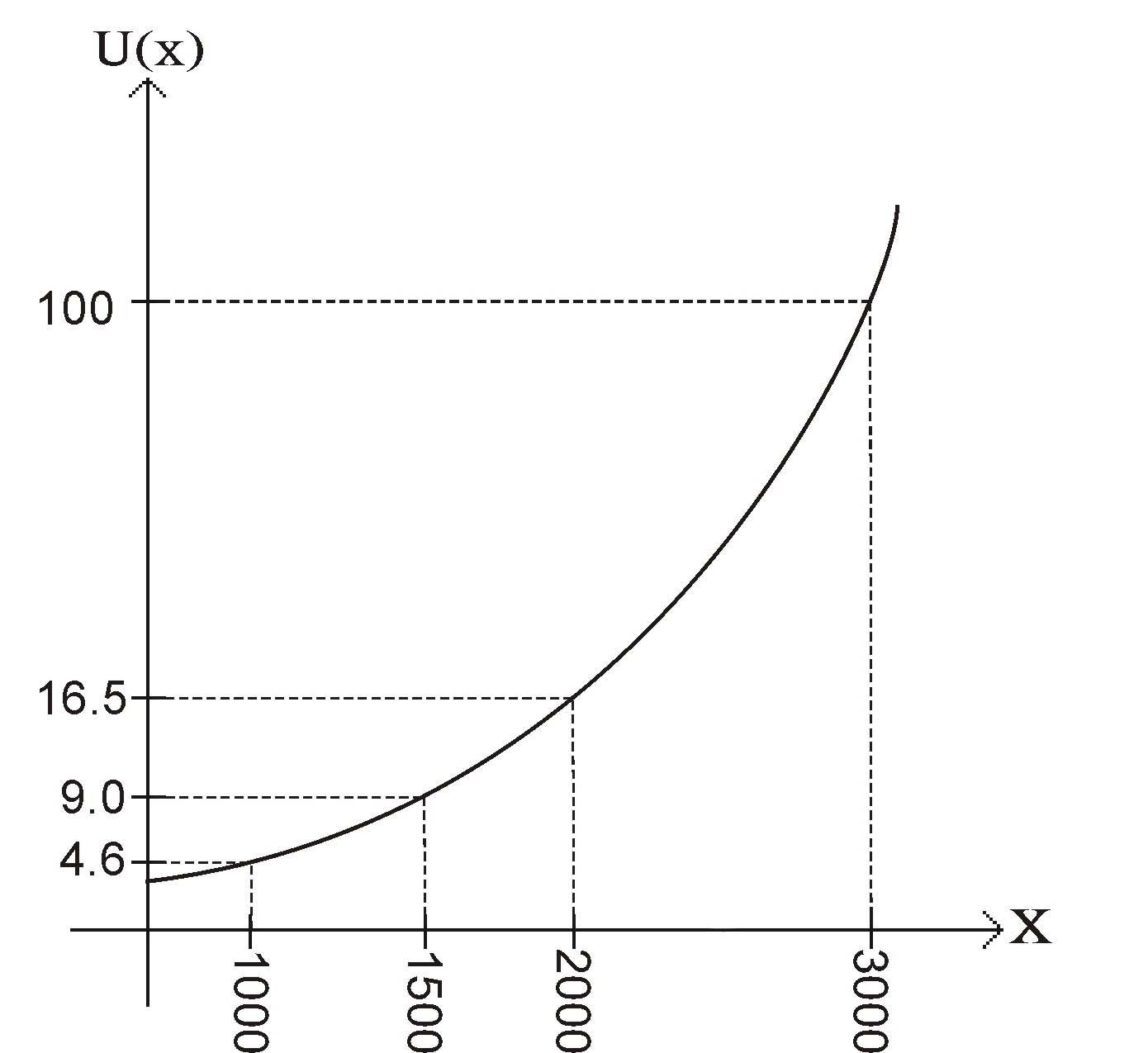
Рисунок 2.4
Особа що приймає рішення:
Прийняти участь у лотереї, яка може дати виграш в 3000 грн. з ймовірністю 0,3, або програш в 1000 грн. з ймовірністю 0,7. Або лотерею, яка обіцяє виграш в 2000 грн., або в 1000 грн. з рівними ймовірностями.
Яке рішення має прийняти особа?
Розв’язання: Очікуваний виграш при першій ситуації знаходимо за формулою (2.2)
1)
![]()
![]()
2)
![]()
![]()
Відповідь.
Краще
прийняти участь у першій лотереї, так
як
![]() .
.
2.3 Контрольні питання
Основні поняття теорії корисності.
Визначення очікуваної корисності.
Ризик та його вимірювання, ризик у відносному виразі.
Дослідження кривих байдужості.
Література: [2, 19-23; 16, 40-45].
ПРАКТИЧНЕ ЗАНЯТТЯ 3
Тема. Метод гілок та границь до розв’язання детермінованих задач теорії прийняття рішень. Розв’язання мінімаксної узагальненої задачі про призначення.
Мета: навчитися застосовувати метод гілок до розв’язання детермінованих задач теорії прийняття рішень. Формувати навички самостійного опанування необхідної наукової літератури.
3.1 Короткі теоретичні відомості.
3.2 Розв’язування задач.
3.3 Контрольні питання.
3.1 Короткі теоретичні відомості
1 Аналіз процедури прийняття рішень
Незважаючи на різноманітність існуючих проблем, виділяють такі основні етапи процедури прийняття рішення:
Визначення цілі.
Формування множини альтернатив (задача визначення множини припустимих рішень).
Побудова оцінки, що дозволяє порівнювати альтернативи (задача оцінювання).
Вибір із множини припустимих рішень найкращого за якістю єдиного рішення (задача оптимізації).
У теорії прийняття рішень сукупність перелічених задач складає загальну проблему прийняття рішень.
Теоретичною основою розв'язання трьох перших задач є системний аналіз, а четвертої - теорія математичного програмування. Прикладні методи розв'язання задач прийняття рішень у різних предметних галузях вивчаються науковим напрямом, який називається дослідження операцій.
Задача
прийняття рішень полягає у виборі із
множини припустимих рішень X
єдиного
кращого (ефективного) рішення (варіанта,
альтернативи) ![]() .
.
Розв'язання цієї задачі пов'язане з формалізацією поняття краще (ефективне) рішення, тобто формуванням деякої оцінки, що дозволяє об'єктивно порівнювати ефективність рішень між собою. Як така оцінка виступають критерії ефективності рішень.
Мета задачі прийняття рішень характеризується частинними властивостями, а рівень її досягнення - їхніми кількісними значеннями. Таким чином, порівняння рішень можна здійснювати за досягнутим рівнем частинних властивостей. Реалізація кожного рішення вимагає в загальному випадку витрат різних ресурсів (фінансових, матеріальних, часових, екологічних і т.д.). У сукупності витрати визначають "ціну", яку необхідно "заплатити" за досягнення цілі.
Визначення. Частинні властивості рішень і пов'язані з ними витрати, зведені до вигляду, який допускає вимірювання у кількісних або якісних шкалах, називаються частинними критеріями.
Множина критеріїв, які оцінюють корисні функціональні властивості рішень, позначається
![]()
Розглянемо
відношення порядку на множині X
виду:
альтернатива хр
домінує
альтернативу хq,
якщо ![]()
Тоді
множину ![]() називають
множиною Слейтера. У цьому випадку
говорять про строге домінування. Тут
називають
множиною Слейтера. У цьому випадку
говорять про строге домінування. Тут
![]() означає
означає
![]() ,якщо
критерій
,якщо
критерій ![]() максимізується,
та
максимізується,
та ![]() -
у протилежному випадку.
-
у протилежному випадку.
Образами
множин ![]() у
результаті відображення
у
результаті відображення
![]() будуть відповідно множини
будуть відповідно множини
![]() .
.
Для
випадку двох критеріїв ![]() та
та
![]() ,
кожний
з яких
,
кожний
з яких
максимізується,
різні ілюстрації образу
![]() безперервної й дискретної множини
припустимих рішень X
наведені
на рис.3.1-3.7.
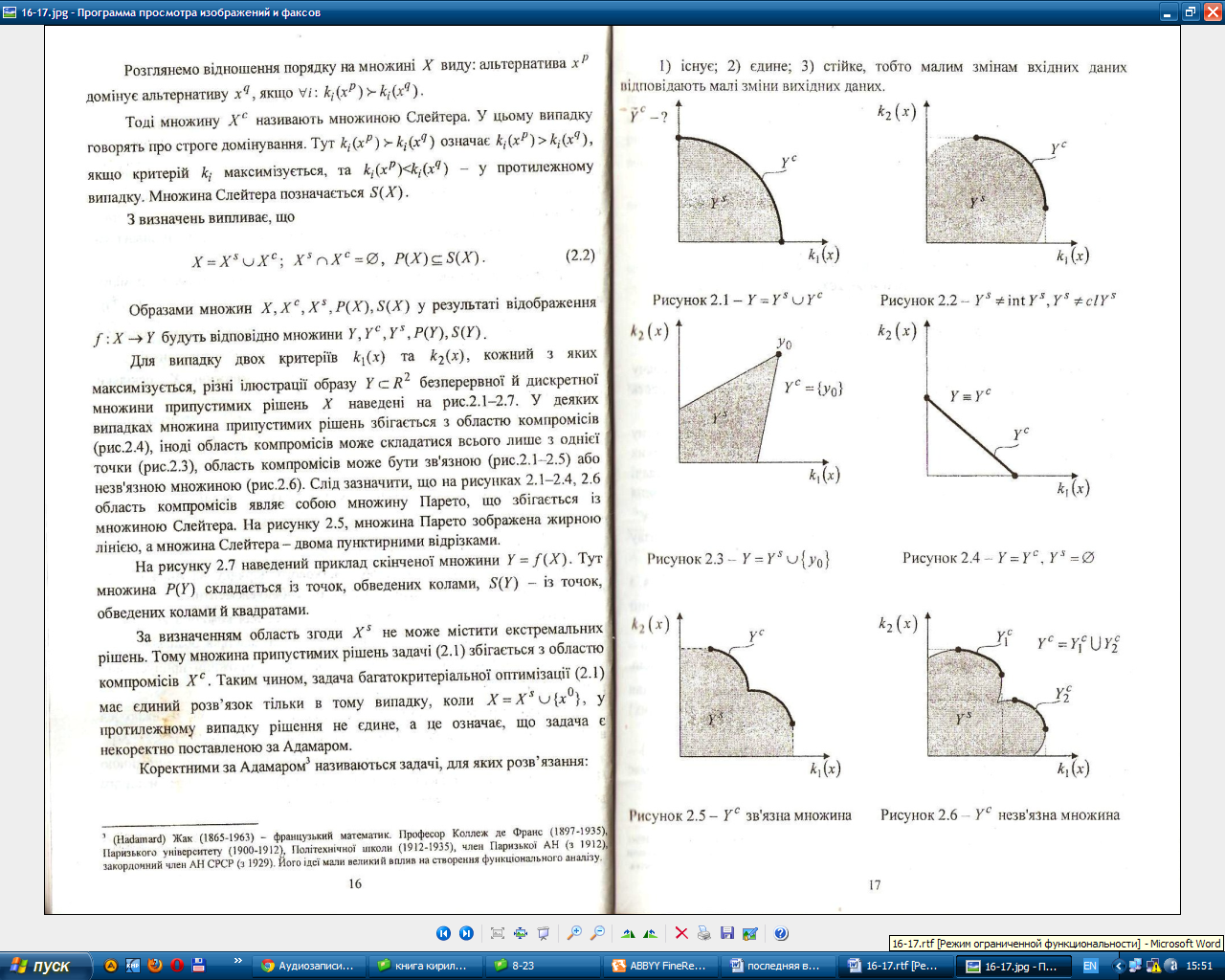
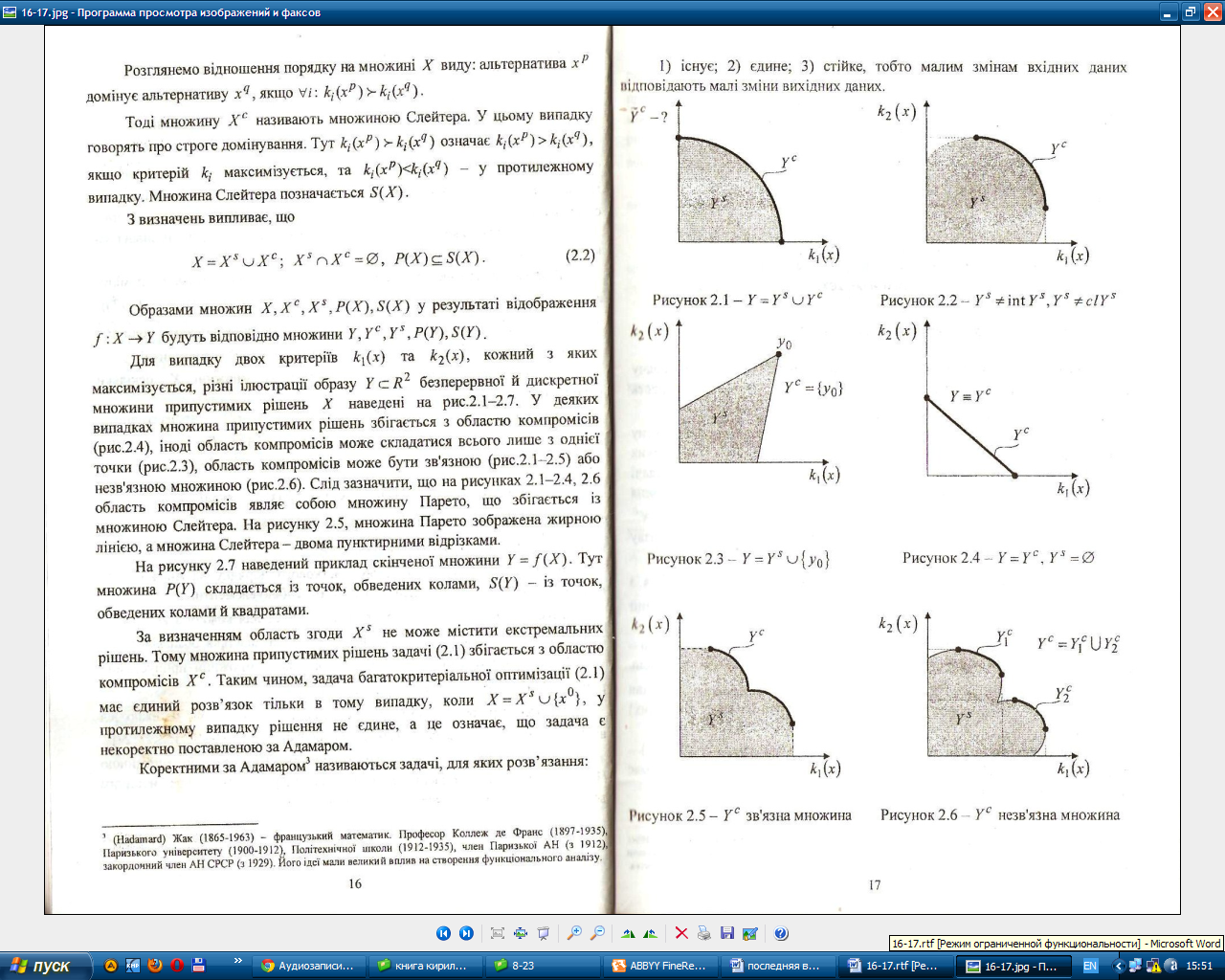
У деяких випадках множина припустимих
рішень збігається з областю компромісів
(рис.3.4), іноді область компромісів може
складатися всього лише з однієї точки
(рис.3.3), область компромісів може бути
зв'язною (рис.3.1-3.5) або незв'язною множиною
(рис.3.6).
Слід зазначити, що на рисунках 3.1-3.4,
3.6
область компромісів являє собою множину
Парето, що збігається із множиною
Слейтера. На рисунку
3.5,
множина Парето зображена жирною лінією,
а множина Слейтера
-
двома пунктирними відрізками.
безперервної й дискретної множини
припустимих рішень X
наведені
на рис.3.1-3.7.
У деяких випадках множина припустимих
рішень збігається з областю компромісів
(рис.3.4), іноді область компромісів може
складатися всього лише з однієї точки
(рис.3.3), область компромісів може бути
зв'язною (рис.3.1-3.5) або незв'язною множиною
(рис.3.6).
Слід зазначити, що на рисунках 3.1-3.4,
3.6
область компромісів являє собою множину
Парето, що збігається із множиною
Слейтера. На рисунку
3.5,
множина Парето зображена жирною лінією,
а множина Слейтера
-
двома пунктирними відрізками.
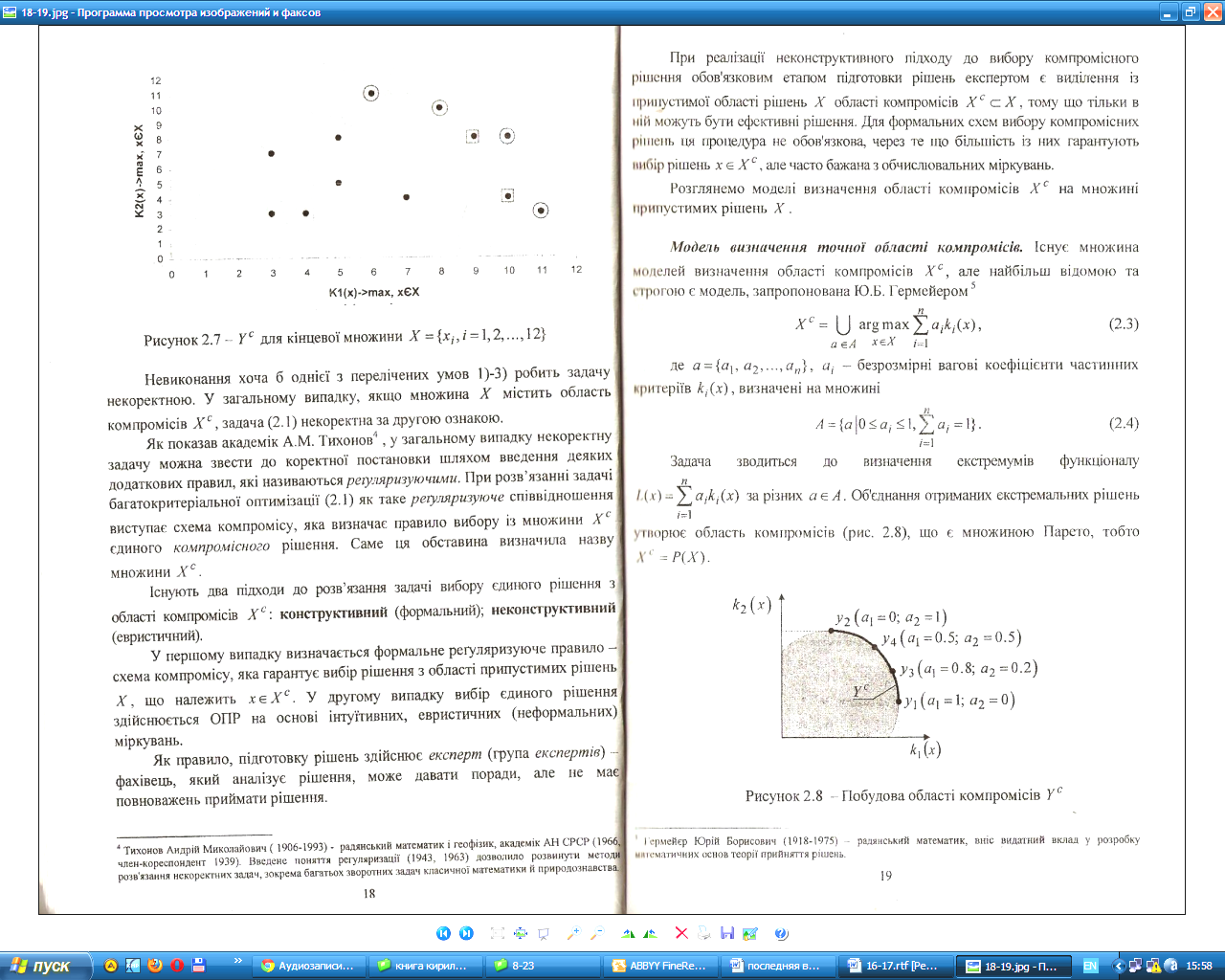
На
рисунку
3.7
наведений приклад скінченої множини
![]() .
Тут
множина
.
Тут
множина ![]() складається
із точок, обведених колами,
складається
із точок, обведених колами, ![]() -
із точок, обведених колами й квадратами.
-
із точок, обведених колами й квадратами.
За
визначенням область згоди ![]() не
може містити екстремальних рішень. Тому
множина припустимих рішень задачі (3.1)
збігається з областю
не
може містити екстремальних рішень. Тому
множина припустимих рішень задачі (3.1)
збігається з областю
компромісів
![]() .
Таким
чином, задача багатокритеріальної
оптимізації (3.1)
має єдиний розв'язок тільки в тому
випадку, коли
.
Таким
чином, задача багатокритеріальної
оптимізації (3.1)
має єдиний розв'язок тільки в тому
випадку, коли ![]() ,
у протилежному випадку рішення не єдине,
а це означає, що задача є некоректно
поставленою за Адамаром.
,
у протилежному випадку рішення не єдине,
а це означає, що задача є некоректно
поставленою за Адамаром.
Коректними за Адамаром3 називаються задачі, для яких розв'язання:
1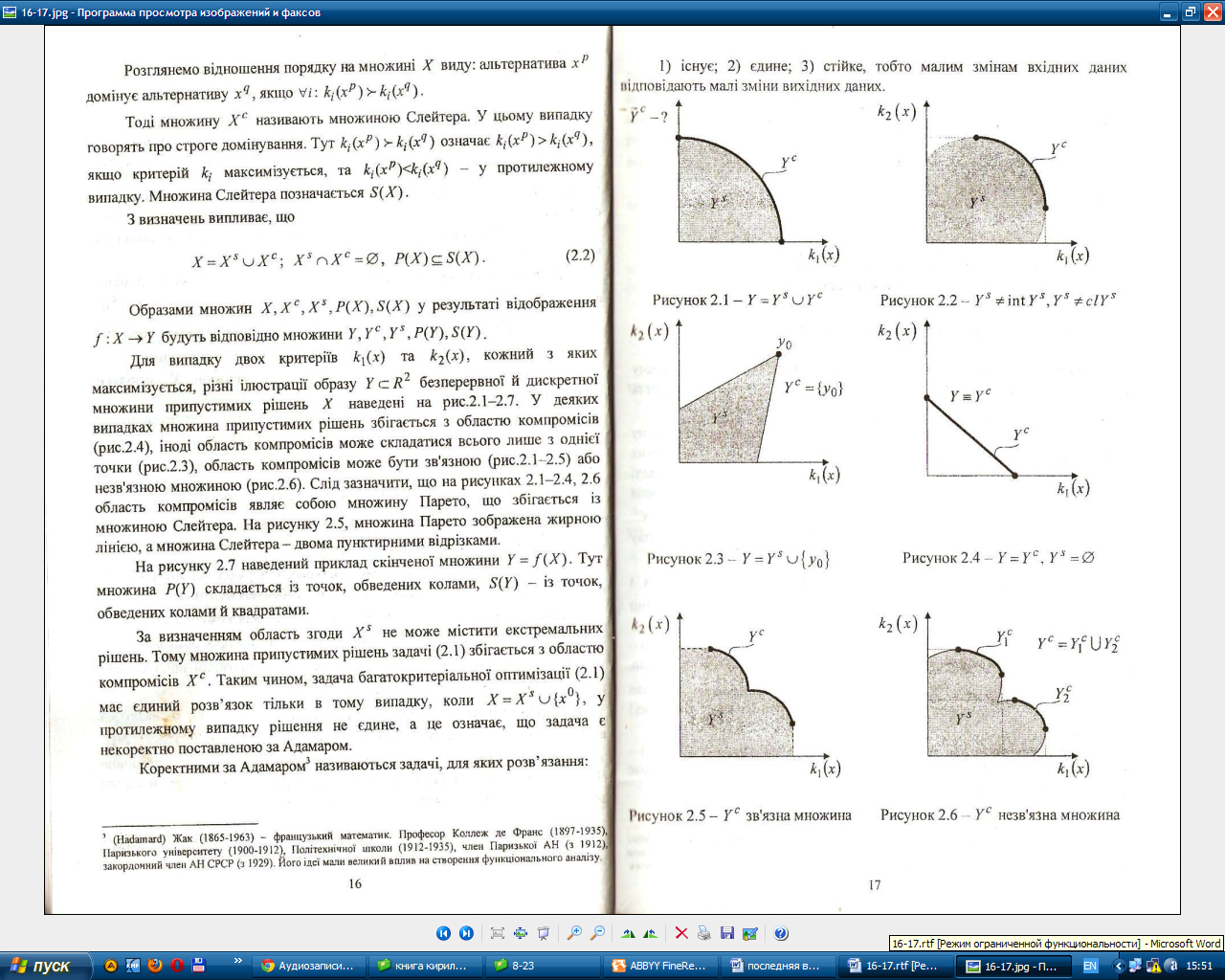 )
існує; 2) єдине; 3) стійке, тобто малим
змінам вхідних даних відповідають малі
зміни вихідних даних.
)
існує; 2) єдине; 3) стійке, тобто малим
змінам вхідних даних відповідають малі
зміни вихідних даних.
Невиконання хоча б однієї з перелічених умов 1-3 робить задачу некоректною. У загальному випадку, якщо множина X містить область
компромісів
![]() ,
задача (3.1)
некоректна за другою ознакою.
,
задача (3.1)
некоректна за другою ознакою.
Як
показав академік A.M.
Тихонов, у загальному випадку некоректну
задачу можна звести до коректної
постановки шляхом введення деяких
додаткових правил, які називаються
регуляризуючими.
При
розв'язанні задачі багатокритеріальної
оптимізації (3.1) як таке регуляризуюче
співвідношення
виступає схема компромісу, яка визначає
правило вибору із множини ![]() єдиного
компромісного
рішення.
Саме ця обставина визначила назву
множини
єдиного
компромісного
рішення.
Саме ця обставина визначила назву
множини
![]() .
.
Існують
два підходи до розв'язання задачі вибору
єдиного рішення з області компромісів
![]() :
конструктивний
(формальний);
неконструктивний
(евристичний).
:
конструктивний
(формальний);
неконструктивний
(евристичний).
У
першому випадку визначається формальне
регуляризуюче правило схема компромісу,
яка гарантує вибір рішення з області
припустимих рішень X,
що
належить
![]() .
У
другому випадку вибір єдиного рішення
здійснюється ОПР на основі інтуїтивних,
евристичних (неформальних) міркувань.
.
У
другому випадку вибір єдиного рішення
здійснюється ОПР на основі інтуїтивних,
евристичних (неформальних) міркувань.
Як правило, підготовку рішень здійснює експерт (група експертів) - фахівець, який аналізує рішення, може давати поради, але не має повноважень приймати рішення.
![]() ,
тому
що тільки в ній
можуть
бути ефективні рішення. Для формальних
схем вибору компромісних рішень ця
процедура не обов'язкова, через те що
більшість із них гарантують вибір рішень
,
тому
що тільки в ній
можуть
бути ефективні рішення. Для формальних
схем вибору компромісних рішень ця
процедура не обов'язкова, через те що
більшість із них гарантують вибір рішень
![]() ,
але часто бажана з обчислювальних
міркувань.
,
але часто бажана з обчислювальних
міркувань.
Розглянемо
моделі визначення області компромісів
![]() на
множині Припустимих рішень X
.
на
множині Припустимих рішень X
.
Модель
визначення точної області компромісів.
Існує
множина
моделей
визначення області компромісів ![]() ,
але
найбільш відомою та строгою
є модель, запропонована Ю.Б. Гермейером
,
але
найбільш відомою та строгою
є модель, запропонована Ю.Б. Гермейером
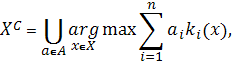
де
![]() ,
,
![]() -
безрозмірні вагові коефіцієнти частинних
критеріїв
-
безрозмірні вагові коефіцієнти частинних
критеріїв
![]() ,
визначені на множині
,
визначені на множині
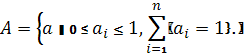
Задача зводиться до визначення екстремумів функціоналу
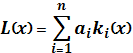 за
різних
за
різних
![]() Об'єднання
отриманих екстремальних рішень
утворює
область
компромісів (рис. 3.8),
що є множиною Парето, тобто
Об'єднання
отриманих екстремальних рішень
утворює
область
компромісів (рис. 3.8),
що є множиною Парето, тобто ![]() .
.
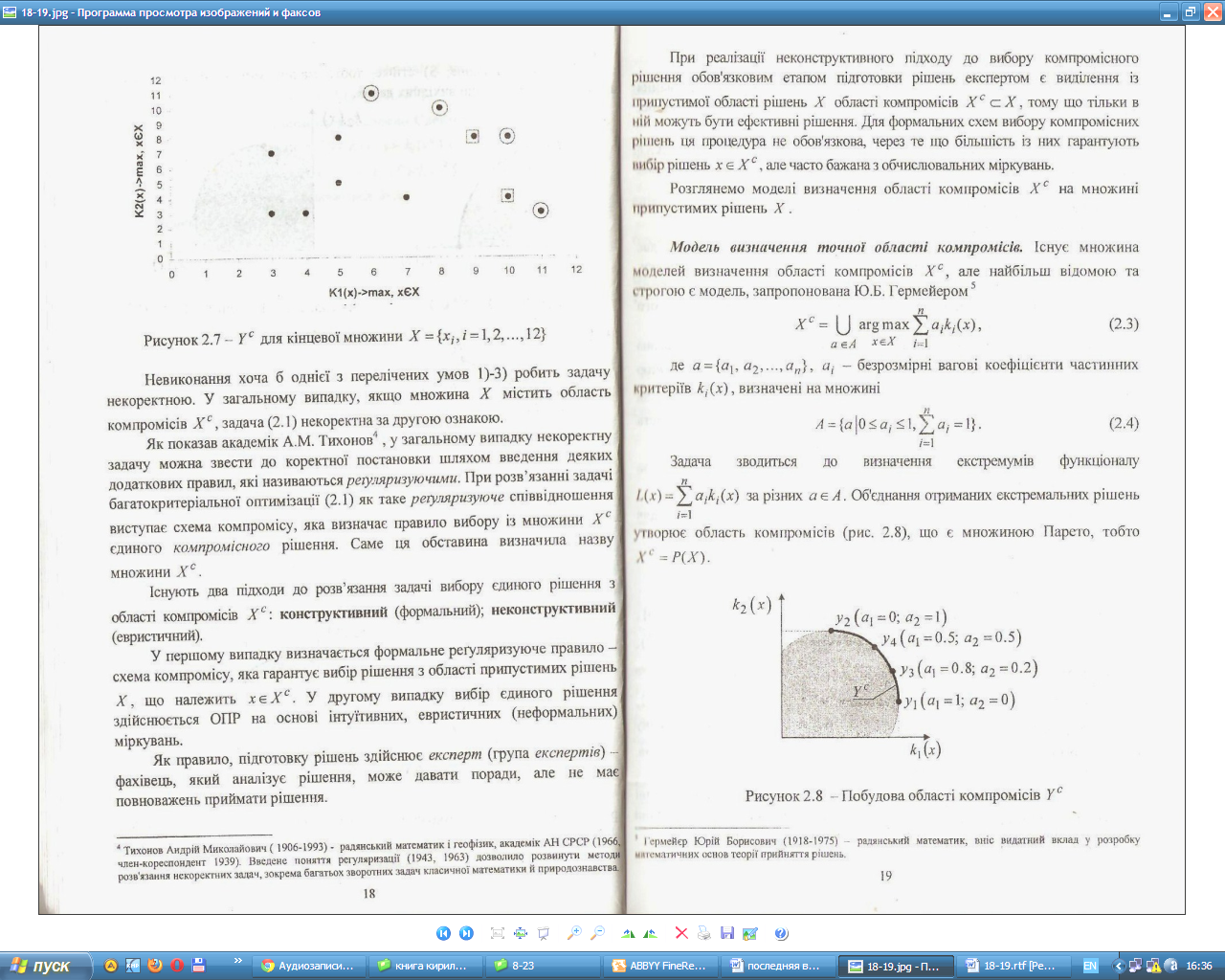
Розглянута модель має дві особливості:
високу трудомісткість, що визначається дискретністю варіювання параметрів
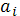 і
нелінійно зростає із збільшенням
числа
n
частинних
критеріїв;
і
нелінійно зростає із збільшенням
числа
n
частинних
критеріїв;модель справедлива тільки в тому випадку, якщо множина X є опуклою. У протилежному випадку необхідно використовувати інші, більш складні моделі.
Якщо множина X скінчена, то зазначені недоліки можна подолати, використовуючи такий підхід.
Наведений нижче алгоритм побудови точної області компромісів дає результати, які залежать від уведеного на множині X відношення порядку. У випадку, якщо введено відношення нестрогого домінування, у результаті отримаємо множину Парето. При використанні відношення строгого домінування - результатом буде множина Слейтера.
Точна
область компромісів для скінченої
множини Х.
Нехай множина
![]() є
скінченою, а кожному
є
скінченою, а кожному ![]() відповідає
вектор
оцінок
відповідає
вектор
оцінок
![]() за всіма критеріями із множини
за всіма критеріями із множини ![]() Побудуємо
точну область
Побудуємо
точну область
компромісів
![]() виходячи
з її визначення.
виходячи
з її визначення.
Із
цією метою здійснимо попарне порівняння
елементів множини X
за
кожним із критеріїв ![]() у
такий спосіб.
у
такий спосіб.
Виберемо
альтернативи ![]() й
порівняємо
й
порівняємо ![]() та
та
![]() для
всіх
для
всіх ![]() .
Можливі такі ситуації:
.
Можливі такі ситуації:
або
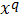 домінує
домінує
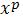 ;
;або
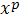 домінує
домінує
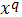 ;
;або
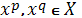 непорівнянні,
тобто існують такі
непорівнянні,
тобто існують такі 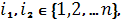
що
![]() та
та ![]() або
або
![]() та
та ![]() тобто висновок про домінування елементів
тобто висновок про домінування елементів
![]() зробити
не можна.
зробити
не можна.
У
результаті порівняння всіх пар елементів
![]()
![]() за
всіма критеріями
за
всіма критеріями ![]() ,
сформуємо точну
,
сформуємо точну
область
компромісів ![]() як
множину всіх недомінованих альтернатив.
Часова складність наведеного алгоритму
має оцінку
як
множину всіх недомінованих альтернатив.
Часова складність наведеного алгоритму
має оцінку ![]()
Коли визначити точну область компромісів на континуальній множині X досить складно або коли потужність скінченої множини X та множини критеріїв велика, то доцільно будувати наближену область компромісів.
Наближена
область компромісів. Вимога
до побудови наближеної області компромісів
![]() полягає
у визначенні множини точок
полягає
у визначенні множини точок ![]() таких, що
таких, що ![]()
тобто область компромісів має належати наближеній області, а наближена область має належати області припустимих рішень.
Зазначимо, що для відповідних образів виконується аналогічне
співвідношення,
тобто ![]()
Один з можливих способів розв'язання цієї задачі при n=2 для безперервних і дискретних множин X є таким.
На
множині припустимих рішень X
послідовно
розв'язуються дві багатокритеріальні
оптимізаційні задачі за кожним частинним
критерієм критерії ![]()
![]()
Для
кожного рішення ![]() обчислюються
значення частинних критеріїв. Позначимо
обчислюються
значення частинних критеріїв. Позначимо
![]()
![]() .
Отримані
результати
заносяться до таблиці 3.1.
.
Отримані
результати
заносяться до таблиці 3.1.
Таблиця
3.1
-
Результати розрахунків для побудови
![]()
|
Рішення |
Значення частинного критерію | |
|
|
| |
|
|
|
|
|
|
|
|
Таким
чином, таблиця 3.1
містить
як найкраще
![]() ,
так і найгірше
,
так і найгірше
![]() значення
частинних критеріїв
значення
частинних критеріїв
![]() .
Множини
значень
.
Множини
значень ![]() та
та
![]() є
відповідними межами інтервалів зміни
значень критеріїв
є
відповідними межами інтервалів зміни
значень критеріїв ![]() при
відображенні наближеної області
компромісів
при
відображенні наближеної області
компромісів ![]() на
простір частинних критеріїв Y.
на
простір частинних критеріїв Y.
Іноді
розв'язком задачі вибору найкращого
рішення за критерієм ![]() є
множина, що складається більш, ніж з
одного елемента, тобто
є
множина, що складається більш, ніж з
одного елемента, тобто
![]()
У цьому випадку вибір єдиного рішення визначається в такий спосіб:
![]()
Образ
![]() наближеної
області компромісів
наближеної
області компромісів ![]() у
просторі Y
задається
таким чином
у
просторі Y
задається
таким чином
![]()
Очевидно, що наближена область компромісів містить у собі не тільки область компромісів, але й деяку підмножину точок області згоди.
Поширимо
описаний спосіб побудови наближеної
області компромісів для
![]() .
.
У випадку, коли множина X опукла, викладена вище схема, розповсюджена на довільне скінчене число критеріїв n, дозволяє одержати наближену область компромісів .
Нехай
X
дискретна.
Проводитимемо порівняння альтернатив
у множині X
за
кожною парою критеріїв із множини
![]() .
Для
цього сформуємо множину пар критеріїв
.
Для
цього сформуємо множину пар критеріїв
![]()
Множина
П містить ![]() елементів.
елементів.
Виберемо
елемент
та
реалізуємо наведений вище спосіб
визначення наближеної області компромісів
для елементів множини X
за
критеріями
![]() У
результаті отримаємо множину
У
результаті отримаємо множину ![]() Виконаємо
цю процедуру для всіх
Виконаємо
цю процедуру для всіх ![]()
Наближену
область компромісів
![]() можна
зобразити у вигляді
можна
зобразити у вигляді
![]()
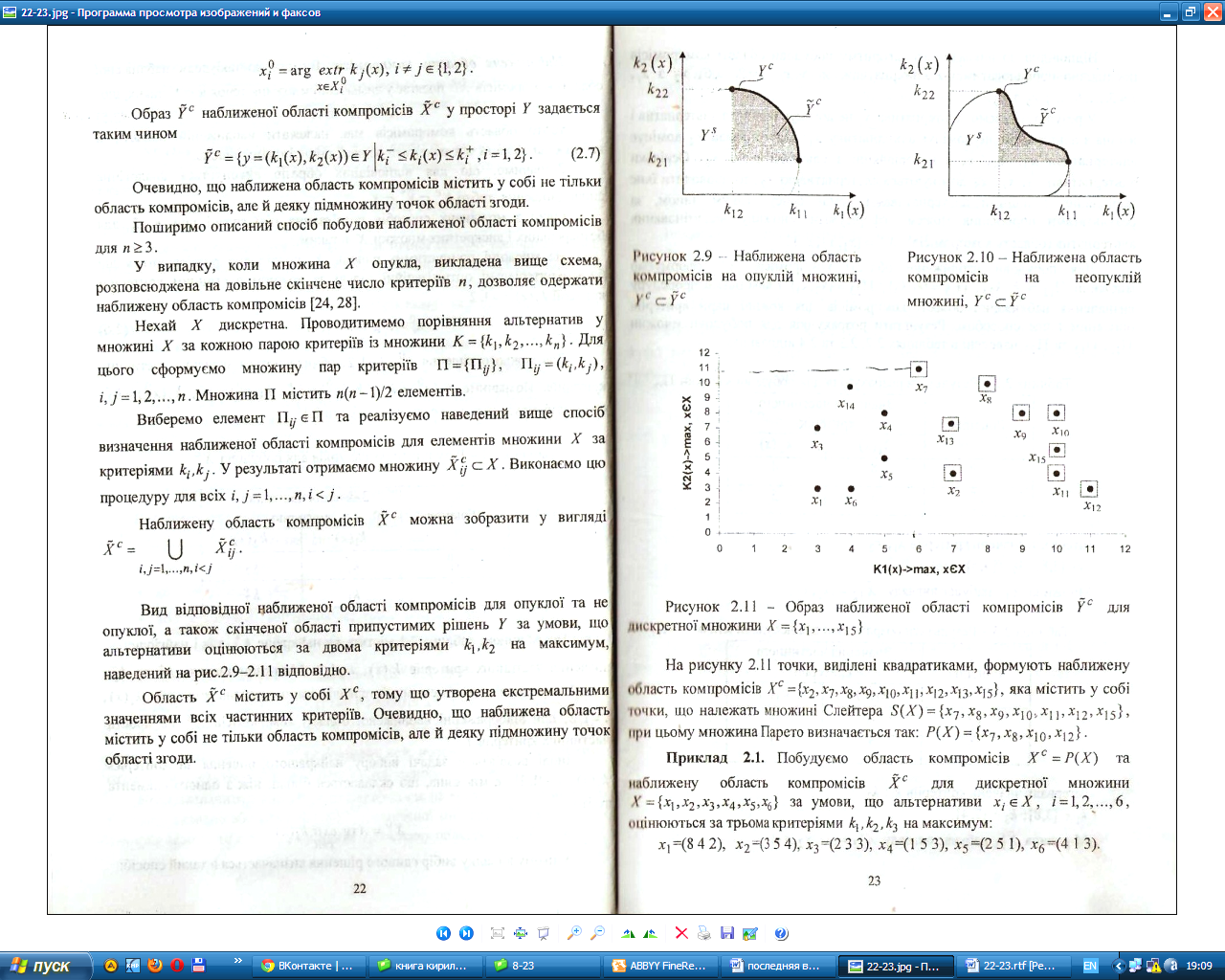
Вид
відповідної наближеної області
компромісів для опуклої та не опуклої,
а також скінченої області припустимих
рішень Y
за
умови, що альтернативи оцінюються за
двома критеріями ![]() на
максимум,
наведений
на рис.3.9-3.11
відповідно.
на
максимум,
наведений
на рис.3.9-3.11
відповідно.
Область
![]() містить
у собі
містить
у собі ![]() тому
що утворена екстремальними значеннями
всіх частинних критеріїв. Очевидно, що
наближена область містить у собі не
тільки область компромісів, але й деяку
підмножину точок області згоди.
тому
що утворена екстремальними значеннями
всіх частинних критеріїв. Очевидно, що
наближена область містить у собі не
тільки область компромісів, але й деяку
підмножину точок області згоди.
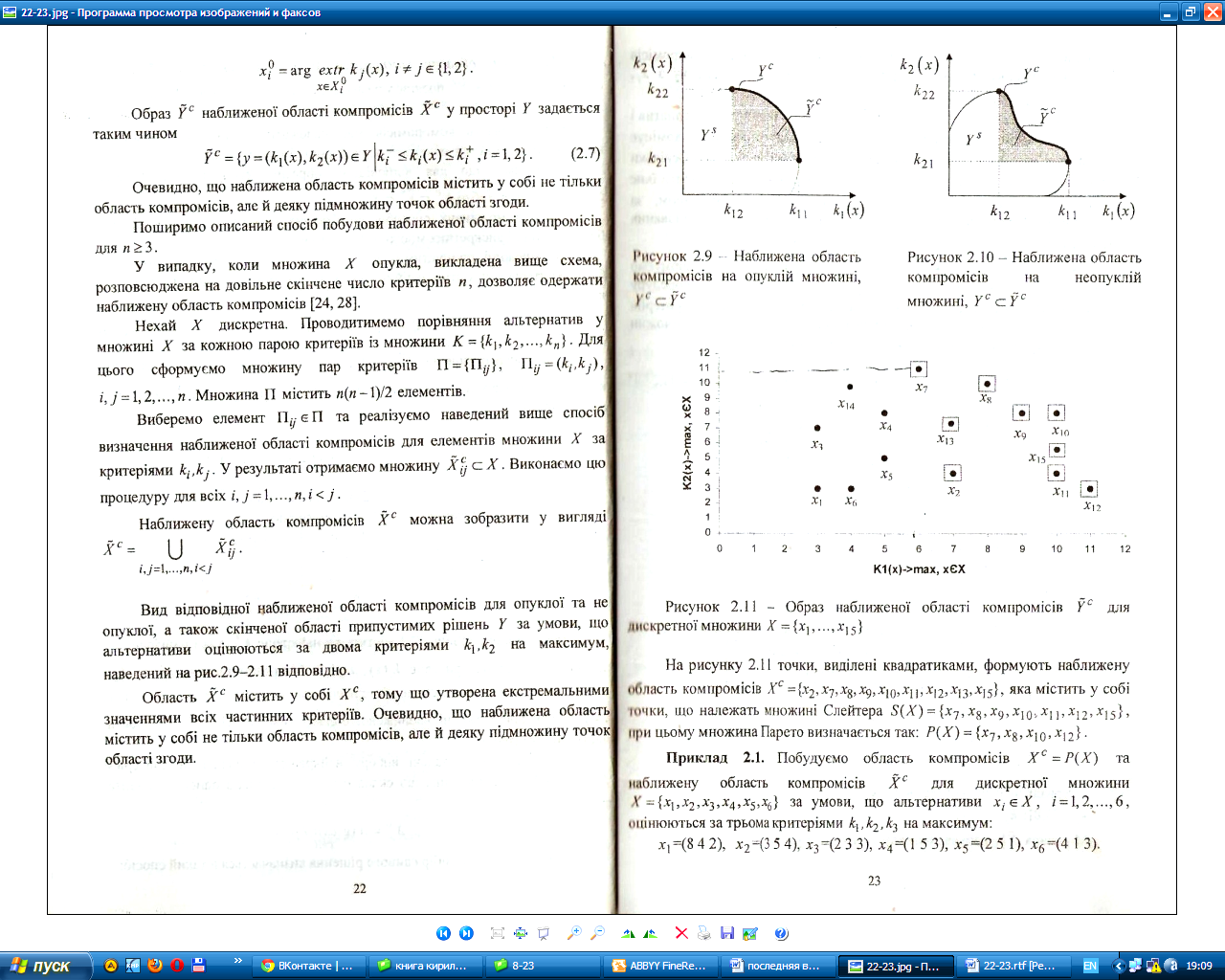
На
рисунку
3.11
точки, виділені квадратиками, формують
наближену область компромісів ![]() яка
містить у собі точки, що належать множині
Слейтера
яка
містить у собі точки, що належать множині
Слейтера ![]() при
цьому множина Парето визначається так:
при
цьому множина Парето визначається так:
![]() .
.
