1.4. Некоторые элементы теории случайных процессов

С точки зрения теории случайных процессов изменения, характеризующие реальные экономические процессы, описываются случайными функциями, значения которых в любой момент времени являются случайными величинами.

Случайные функции одной независимой переменной, за которую принимают время, называют случайными процессами.

Последовательность наблюдений Y(t₁), Y(t₂), …, Y(t_n) некоторого экономического процесса называют реализацией случайного процесса. Последовательность наблюдений {Y(t_i)}, полученных в равностоящие моменты времени, называют временным или динамическим рядом [21].

С каждым случайным процессом обычно связывают несколько неслучайных функций: математическое ожидание, дисперсию, автокорреляционную и взаимную корреляционную функции.

Математическим ожиданием случайного процесса называют неслучайную функцию времени М[], значения которой при t = t_i равны математическому ожиданию случайной величины . Это значит, что математическое ожидание случайного процесса есть некоторая средняя функция, вокруг которой варьируются результаты наблюдений.

Степень рассеивания этих наблюдений вокруг среднего значения характеризуется дисперсией случайного процесса.

Дисперсией случайного процесса называется неслучайная функция времени D [], значения которой для каждого момента времени t = t_i равны дисперсии соответствующих случайных величин.

Таким образом, при рассмотрении математического ожидания и дисперсии случайного процесса видно, что процесс разбивается на некоторую систематическую составляющую (среднюю) и отклонения от нее. При анализе временных рядов это находит свое отражение в представлении ряда Y_t в виде суммы

Y_t = F_t + Е„

где F_t — неслучайная функция времени, характеризующая систематическую составляющую;

Е_t — случайная компонента с нулевым математическим ожиданием и дисперсией D [].

Для полной характеристики случайного процесса применяется автокорреляционная функция , которая представляет собой множество коэффициентов корреляции между временным рядом Y_t и этим же рядом, сдвинутым во времени на величину τ. Нормированная автокорреляционная функция вычисляется по формуле

(1.9)

где τ = 0, 1, 2, …, n-2; t = 1, 2, …, n-τ.

Автокорреляционная функция (1.9) называется нормированной, так как =1. Величину τ называют сдвигом. Сдвиг, которому соответствует наибольший коэффициент автокорреляции, называют временным лагом. График нормированной автокорреляционной функции называют коррелограммом. Он показывает, как часто и с каким запаздыванием изменение показателя y_t сказывается на последующих значениях этого показателя, при этом значения автокорреляционной функции могут колебаться от -1 до 1.

Автокорреляционная функция для случайной составляющей E_t имеет следующий вид:

(1.10)

Для одновременного сравнения и анализа двух случайных процессов по их заданным реализациям {Y_t} и {Х_t} используют взаимную корреляционную функцию. Нормированная взаимная корреляционная функция вычисляется по формуле.

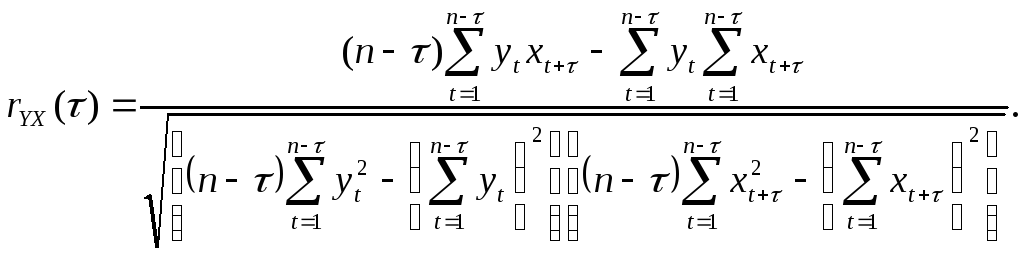(1.11)

Соответственно при вычислении взаимной корреляционной функции между случайными компонентами E_t и Z_t эта формула примет следующий вид:

(1.12)

Применение методов теории случайных процессов для анализа экономических временных рядов в значительной степени связано с проблемой исследования случайной составляющей E(t) и сравнения ее с другими случайными величинами, обладающими изученными свойствами. Это объясняется тем, что при краткосрочном и среднесрочном прогнозировании результаты прогнозов тесно связаны со случайной компонентой, в то время как при долгосрочном прогнозировании основное значение имеет определение тенденций и взаимосвязей между факторами.

В настоящее время наиболее изученными являются стационарные случайные процессы, которые протекают во времени приблизительно однородно и имеют вид непрерывных случайных колебаний вокруг некоторого среднего уровня, причем ни характер этих колебаний, ни средняя амплитуда со временем существенно не изменяются. Любой стационарный процесс можно рассматривать как процесс, продолжающийся во времени неопределенно долго. Поэтому при проведении исследований в качестве начала отсчета можно выбирать любой момент времени, причем на любом временном интервале должны быть получены одни и те же вероятностные характеристики. Поэтому стационарным процессом, в широком смысле слова, можно назвать такой случайный процесс, у которого математическое ожидание постоянно, а автокорреляционная функция не зависит от времени, и для этого процесса выполняются следующие соотношения:

где τ = t_i - t_j.

Величина автокорреляционной функции не зависит от начала отсчета, а зависит только от величины сдвига τ. Значение определяет постоянный уровень, относительно которого варьируют значения временного рядаY_t, а постоянная величина σ² характеризует размах этой вариации. Поскольку закон распределения вероятностей случайной величины одинаков для всехt, то основные характеристики стационарного случайного процесса могут быть оценены по наблюдениям y₁, y₂, …, y_n как

В экономической практике в большинстве случаев приходится иметь дело с процессами, имеющими вполне определенную тенденцию развития явления во времени. Такие процессы называются нестационарными. Характеристики нестационарных случайных процессов меняются во времени, т. е. зависят от начала отсчета. В ряде случаев эти процессы на определенных интервалах времени условно могут быть приняты за стационарные. Тогда на них могут быть перенесены все основные выводы стационарных случайных процессов. Те экономические процессы, которые содержат явно выраженную тенденцию, можно преобразовать в стационарные путем исключения тенденции и периодических колебаний из временных рядов, если таковые имеются.

Таким образом, исходя из вышеизложенного можно сформулировать основные задачи статистического анализа временного ряда.

По имеющимся значениям y₁, y₂, …, y_n анализируемого временного ряда требуется:

а) определить, какие из неслучайных функций F_t, К_t, S_t присутствуют в аддитивном разложении (1.6);

б) построить „хорошие" оценки для этих неслучайных функций и в первую очередь определить наилучшим образом оценку долговременной составляющей (тенденции), которая отражает основные закономерности изменения исследуемой характеристики во времени;

в) подобрать модель, адекватно описывающую поведение случайной компоненты Е_t, и статистически оценить ее параметры.

Успешное решение этих задач является основой для достижения конечных целей исследования, и в первую очередь для построения кратко- и среднесрочного прогнозов значений временного ряда.