3.3. Проверка гипотезы о нормальности случайного компонента

В ряде случаев при применении некоторых методов для прогнозирования явлений необходимо проверить гипотезу о том, что отклонения от тренда или соответствующей модели подчиняются закону нормального распределения. А так как временные ряды, как правило, невелики (не более 50 наблюдений), то проверка распределения на нормальность может быть лишь приближенной и проводить ее можно с помощью исследования показателей асимметрии, и эксцесса. При нормальном распределении эти показатели должны быть равны нулю. Но так как отклонения от тренда представляют собой лишь выборку из некоторой генеральной совокупности, то определяются только выборочные характеристики асимметрии и эксцесса и их ошибки по следующим формулам:

; (3.2)

; (3.3)

; (3.4)

(3.5)

где А — выборочная характеристика асимметрий;

Э — выборочная характеристика эксцесса;

—среднеквадратическая ошибка выборочной характеристики асимметрии;

—среднеквадратическая ошибка выборочной характеристики эксцесса.

Если одновременно выполняются следующие неравенства:

(3.6)

то гипотеза о нормальном характере распределения случайного компонента не отвергается. Если же выполняется хотя бы одно из неравенств

то гипотеза о нормальном характере распределения отвергается.

3.4. ПРОВЕРКА ГИПОТЕЗЫ О СТАЦИОНАРНОСТИ СЛУЧАЙНОГО КОМПОНЕНТА

Если гипотеза о том, что отклонения от тренда представляют собой стационарный случайный процесс, подтверждается, то при прогнозировании случайного компонента могут применяться методы прогноза для стационарных случайных процессов.

Основным условием стационарности случайного процесса (см. п. 1.4) является зависимость автокорреляционной функции только от разности аргументов τ= t_i - t_j.

Для проверки гипотезы о том, что значение автокорреляционной функции зависит не от выбора начала отсчета наблюдений, а от величины сдвига τ, выполняются следующие действия.

1. Для случайного компонента E_t находятся значения автокорреляционной функции (верхний индекс означает число наблюдений, при котором вычисляется автокорреляционная функция).

2. Затем исключается одно из крайних наблюдений (первое или последнее), и вычисляется новая автокорреляционная функция .

3. Подобным образом исключаются k (k = 0, 1, 2, …,K) наблюдений и вычисляются значения (К + 1) автокорреляционных функций. Таким образом, получим τ групп коэффициентов автокорреляции, в каждую из которых входит (К + 1)-коэффициент. Для стационарного случайного процесса коэффициенты автокорреляции, входящие в одну группу, должны быть однородными.

4. Проверка на однородность заключается в том, что для каждого , входящего в τ-ю группу, вычисляется величина z-критерия по формуле

.

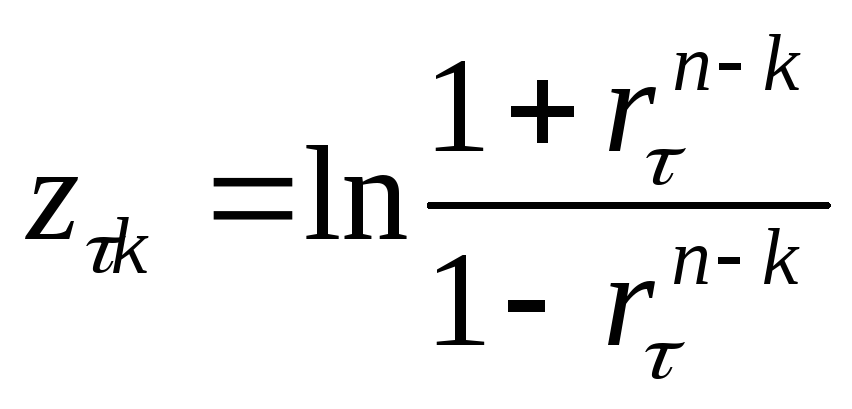Затем для каждой группы τ рассчитывается среднее значение :

. (3.7)

Также для каждой группы г вычисляется величина

(3.8)

и сравнивается со значением, взятым из таблицы χ²-распределения, при определенном уровне значимости и с k степенями свободы. Если вычисленная по формуле (3.8) величина меньше табличного χ², то гипотеза об однородности τ-й группы коэффициентов автокорреляции не отвергается.

4. Если гипотеза об однородности не отвергается для всех групп, то можно принять, что автокорреляционная функция зависит только от разности аргументов τ, т. е. случайный компонент представляет собой стационарный случайный процесс.