Измерение связи между признаками с помощью корреляционной решетки

Коэффициент линейной корреляции Пирсона наиболее быстро определяется по вышеприведенной формуле на небольшом числе наблюдений по данным, которые представлены в виде простых вариационных рядов, где частоты, как известно, равны единице. Прямой путь вычисления коэффициента корреляции при парной связи осуществляется при небольшом числе наблюдений на основе использования средних величин и отклонений от них. Однако когда имеется большое число наблюдений и данные сгруппированы с определенным интервалом, т.е. представлены в виде взвешенных сгруппированных вариационных рядов, вычисление производится по другой формуле и является более трудоемким. Техника вычисления осуществляется непрямым способом на основе метода Бравэ.

Для вычисления коэффициента корреляции при этих условиях необходимо строить корреляционную решетку, или таблицу сопряженности. Такие условия на практике чаще всего встречаются при изучении и оценке физического развития отдельных групп населения.

Рассмотрим методику вычисления коэффициента корреляции на примере определения связи между ростом и массой тела у 8-летних девочек (см. образец решения задачи). Результаты исследования в таблице сопряженности могут быть представлены в одинаковом числе групп для подлежащего и сказуемого таблицы. В данной задаче сведения, приведенные в подлежащем, распределены по росту на 11 групп, а данные, содержащиеся в сказуемом, разделены по массе тела на 9 групп. Можно выделить следующие этапы вычисления.

1. Сначала полученные в исследовании результаты записывают по общепринятым правилам в виде двух сопряженных сгруппированных рядов:

по росту – 106-107,9 см ит.д.;

по массе тела – 16-16,9 кг, 17-17,9 кг и т.д.

2. Затем для каждой группы определяют середину интервала (V₁). В случае

непрерывных вариационных рядов середина интервала определяется как полусумма начальных вариантов двух соседних групп. Так, в ряду x для первой группы (строки подлежащего) V=для следующей группыV=и т.д.

Образец решения задачи

по вычислению коэффициента корреляции с помощью корреляционной решетки

Рост, см (x)		Масса тела, кг (y)
		16- 16,9	17- 17,9	18- 18,9	19- 19,9	20- 20,9	21- 21,9	22- 22,9	23- 23,9	24- 24,9	Px	axi*	Px · ax	Px · ax2	Px · ay	Px · ay · ax
Vx	Vix	Середина интервала (Viy)
		16,5	17,5	18,5	19,5 (Ay)	20,5	21,5	22,5	23,5	24,5
106-107,9	107	-	2	3	-	1					6	-2	-12	24	-6	12
108-109,9	109	2	2	5	4						13	-1	-13	13	-15	15
110-111,9	111(Ax)	8	9	7	19	1	1	-	-	1	46	0	0	0	-41	0
112-113,9	113	-	4	5	5	1	3	2	-	1	21	1	21	21	5	5
114-115,9	115	1	-	3	11	-	4	-	2	-	19	2	38	76	2	4
116-117,9	117	-	-	-	3	2	-	2	2	-	9	3	27	81	16	48
118-119,9	119	-	-	1	6	1	2	1	4	1	16	4	64	256	28	112
120-121,9	121	-	2	-	-	-	8	8	-	-	18	5	90	450	36	180
122-123,9	123	-	-	-	-	2	-	2	-	1	5	6	30	180	13	78
124-125,9	125	-	-	-	-	-	-	-	-	2	2	7	14	98	10	70
126-127,9	127	-	-	-	-	-	-	-	-	1	1	8	8	64	5	40
Py		11	19	24	48	8	18	15	6	7	Σ156	-	Σ267	Σ1263	Σ53	Σ564
ay		-3	-2	-1	0	1	2	3	4	5
Py · ay		-33	-38	-24	0	8	36	45	24	35	Σ53
Py · ay2		99	76	24	0	8	72	135	96	175	Σ685

* a_xⁱ – сокращенные на величину интервала вычисленные условные отклонения (пояснения см. в тексте).

В сказуемом ряду (ряду y) для первой группы V=, для второй группыV= и т.д.

3. Дальнейшие вычисления можно производить непосредственным методом, но лучше одним из ускоренных способов. Рассмотрим вычисление по способу условной средней (или способу моментов). Для этого любая середина интервала выбирается за условную среднюю (А). В задаче среди данных по росту за условную среднюю (А_x) выбрана середина интервала, наиболее часто (P-46) встречающаяся и равная 111 см, а по массе тела за условную среднюю (A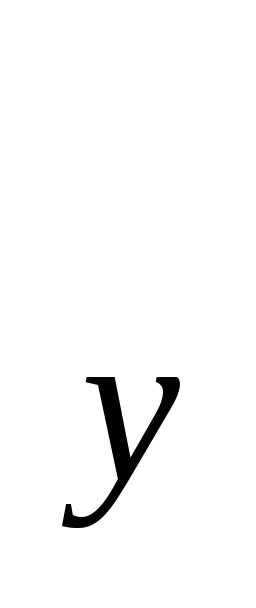) принята середина интервала, равная 19,5 кг.

4. Определяют условные отклонения по формуле: a_x=V

a и т.д., для ряда y:V a и т.д. Для данных по росту величины середины интервалов получаются кратными 2: 0, 2, 4, 6, 8, 10, 12, 14, 16, так как варианты объединены в группы с интервалом, равным двум единицам. Рационально в этом случае полученные условные отклоненияa_x сократить на 2, т.е. сократить на интервал, и записать сокращенные данные, которые и приведены в условии задачи (таблица, столбец “a” ). Таким образом: для первой группы по росту , для второйи т.д.

Для данных по массе тела этих сокращений делать не надо, так как интервал равен 1.

5. Далее для каждого ряда производят в указанной последовательности

умножение полученных данных, как показано в условии задачи (в таблице), и определяют сумму вычисленных произведений:

а) отклонения умножаются на частоты () и () и определяются суммы:;;

б) перемножают условные отклонения (и) на соответствующие произведения (;), суммируют полученные произведения (;);

в) для каждой группы умножают наи суммируют полученные результаты:;

г) определяют произведения и находят их сумму:.

На основании вышеуказанных расчетов, которые проводятся обязательно с помощью таблицы сопряженности и заносятся в нее, далее осуществляется вычисление соответствующих параметров отдельно для ряда x (по росту) и для ряда y (по массе тела).

6. Производят расчет для данных ряда x (по росту), где n=156, условная средняя

A_x =111 см, i_x =2 (другие параметры имеются в таблице).

По способу моментов сначала определяют среднюю арифметическую:

Затем вычисляют среднее квадратическое отклонение:

=,

где («ню») – момент (или поправка) в первой степени;- момент или поправка) во второй степени.

7. Аналогично рассчитывают параметры для ряда y (по массе тела), в котором n также равняется 156 единицам наблюдения, А =19: кг, интервал i_y = 1, а момент первой степени равен:

Вычисляют среднюю массу тела:

Определяют момент второй степени:

Рассчитывают среднее квадратическое отклонение для этого признака:

8. Определяют коэффициент корреляции Пирсона на основе вышепроведенных вычислений и исходных величин:

,

где - момент первой степени для рядаx ; - момент первой степени для рядаy ; и- соответствующие этим рядам средние квадратические отклонения, деленные наi (на интервал):

и .

Подставляя имеющиеся данные в эти формулы, получают:

Подставляя необходимые величины в формулу, получают коэффициент корреляции:

Полученный коэффициент корреляции свидетельствует, что между ростом и массой тела у 8-летних девочек существует прямая зависимость средней силы. Достоверность коэффициента при большом числе наблюдений (ориентировочно 30 – 100 единиц) определяется при помощи средней ошибки по формуле:

Так как средняя ошибка коэффициента меньше его величины более чем в 3 раза, то полученные статистические данные и сделанные на основе их выводы являются не случайными, а репрезентативными, о чем свидетельствует и доверительный критерий t :

Имея данные, рассчитанные по корреляционной решетке, можно определять и другие параметры – коэффициенты вариации и коэффициенты регрессии.

Коэффициент вариации С_v по росту равен:

по массе тела равен:

Полученные коэффициенты свидетельствуют, во-первых, о том, что колеблемость результатов измерений роста и массы тела низкая, т.е. данные получены на статистически однородной совокупности в том и другом случае, Во-вторых, по массе тела колеблемость данных является относительно большей, чем по росту (>), следовательно, признак роста у 8-летних девочек является более стабильным, а второй признак (масса тела) является более вариабельным, т.е. может колебаться в больших пределах.

Коэффициент регрессии для массы тела по росту определяют по формуле:

Это означает, что с увеличением роста на 1 см масса тела у 8-летних девочек увеличивается в среднем на 1,4 кг.