Коэффициент корреляции Пирсона

При наличии прямолинейной связи между взаимосвязанными количественными признаками, особенно при большом числе наблюдений, рациональнее прибегать к параметрическим методам оценки, которые требуют вычисления определенных параметров: средней величины, средне-квадратического отклонения (), средней ошибки. При этом вычисление связи проводится по методу квадратов на основании корреляционной решетки (таблицы сопряженности), если имеется большое число наблюдений. При числе наблюдений менее 30 сравниваемых пар коэффициент линейной корреляции К. Пирсона определяется по формуле:

r_xy =

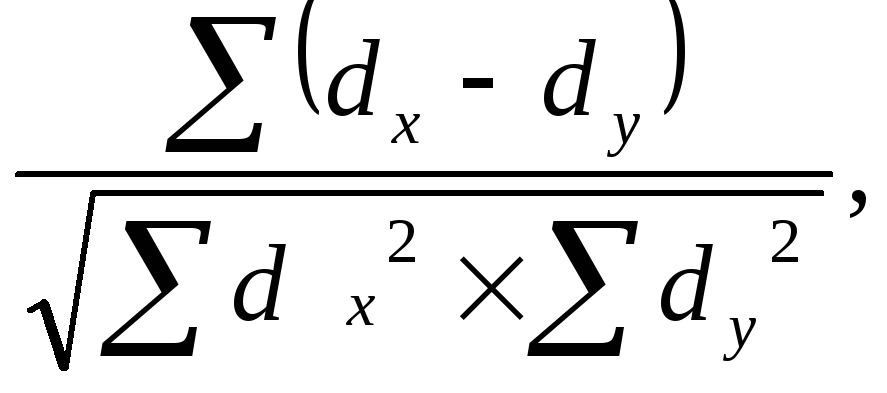
где r_xy - коэффициент линейной корреляции между двумя признаками x и y; d - отклонения от средних арифметических данных ряда x и ряда y.

Образец решения задачи

Исходные данные и параметры расчета коэффициента линейной корреляции

Номера региона	Охват населения прививками,% x	Заболеваемость на 10 000 человек населения y	dx	dy	dx2	dy2	dxdy
1 2 3 4 5	15,0 20,0 25,0 30,0 35,0	22,0 28,0 18,0 14,0 10,0	10 5 0 - 5 - 10	- 3,6 - 9,6 0,4 4,4 8,4	100,0 25,0 0 25,0 100,0	12,96 92,16 0,16 19,36 70,56	- 36 - 48 0 - 22 - 84
Всего	25,0	18,4			250	195,2	- 190

Порядок вычисления

1. Находят усредненные данные для обоих рядов (x и y), т.е. средние

величины по формуле (для коэффициентов определяют общие коэффициенты):

М =

2. Определяют отклонения от этих усредненных величин (d_x = M_x – x,

d_y = M_y -y) с обозначением соответствующего отрицательного знака. В данном случае: d_x = 25 - 15 =10;d_x= 25 -20 =5 и т.д. Для ряда y : d_y =18,4 – 22,0 = - 3,6;d_y = 18,4 – 28 = - 9,6 и т.д.

3. Возводят полученные результаты в квадрат и получают суммы этих квадратов

(иd_y).

4. Находят произведения каждого d_x на d_y и получают их сумму ().

5. Подставляют полученные данные в формулу:

r_xy =

При определении коэффициента линейной корреляции Пирсона на программируемых калькуляторах надо иметь два основных документа: специальную программу вычисления и инструкцию по ее применению. Для персональных компьютеров разработаны также специальные программы вычисления на языке Бейсик.

Так как полученные коэффициенты определяются, как правило, на материалах выборочного исследования, то всегда необходимо убеждаться в степени их надежности. Представительность (репрезентативность) коэффициента линейности корреляции также может определяться по специальным таблицам (приложение 2) или ориентировочно – по средним ошибкам, которые должны для обоснования значимости связи быть в 3 раза меньше своего коэффициента корреляции. Коэффициент считается представительным, если полученная величина его превышает критическое значение при p< 0,05 и заданном числе степеней свободы n, которое равняется n – 2. Полученная в задаче величина 0,86 превышает критический уровень 0,75 при n = 5 и p< 0,05.

При отсутствии таблицы критических значений коэффициентов корреляции представительность коэффициента может быть определена по величине средней ошибки m (при числе парных наблюдений менее 100):

m_r=

Можно для определения средней ошибки использовать и более упрощенную формулу:

m_r=

Коэффициент корреляции будет достоверен лишь в том случае, когда он превышает свою ошибку в 3 – 4 раза. Оценку значимости проводят и по t- критерию, его величину определяют по формуле:

t =r при n<100.

Для нашей задачи:

t = 0,86

Так как t > 2, то это говорит о достаточной достоверности влияния прививок на уровень заболеваемости и о значимости полученных результатов. Оценку критерия t можно давать и по специальным оценочным таблицам, в Соответствии с которыми при уровне значимости p , равном 0,05 (5%), и числе степеней свободы 4 и 5 этот критерий должен равняться соответственно 2,776 или 2,571. В данном случае доверительный критерий t больше указанных табличных значений, следовательно, получены хорошие результаты. Достоверность корреляции доказана, нулевая гипотеза предусматривает отсутствие корреляционной связи. Если полученный коэффициент корреляции не удовлетворяет принятому уровню значимости, т.е. его вероятность ниже 0,95, то это является основанием для признания нулевой гипотезы правильной.

Правильная трактовка коэффициентов корреляции предполагает нормальное распределение сопряженных величин коррелируемых рядов x и y. Однако при малом числе наблюдений и сравнительно сильной корреляции вычисленный коэффициент корреляции не всегда будет точной оценкой для генеральной совокупности. В этих случаях коэффициент r целесообразно заменить преобразованной величиной Z (преобразование Фишера).

Форма распределения величины Z почти не отличается от формы нормального распределения, так как мало зависит от численности выборки и значения r в генеральной совокупности. Только с помощью величины Z можно определить достоверность различий между двумя коэффициентами корреляции, а также объединить данные по нескольким корреляциям. Преобразование r в Z проводится по специальным таблицам, имеющимся в различных пособиях по статистике.

В заключение следует обратить внимание на возможность пользования следующих наиболее доступных и простых формул определения средних ошибок коэффициентов корреляции.

1. Ошибка коэффициента корреляции, вычисленного по методу Спирмена:

m=

2. Ошибка коэффициента корреляции, вычисленного обычным методом Пирсона:

m_r=