4.2. Аналитическая модель рядов динамики

4.2.1. Факторы, влияющие на формирование значений уровней рядов динамики

Рассмотрим факторы, влияющие на формирование значе­ний уровней рядов динамики.

1. Долговременные факторы, формирующие общую в дли­тельной перспективе тенденцию развития признака. Результат этого действия определяется с помощью неслучайной монотон­ной функции тренда На рис. 4.2 изображена линейная функция тренда.

2. Сезонные факторы, влияющие на уровни ряда динамики и определенный период времени (сезон), причем подобные вме нения для данного сезона можно считать постоянной величи ной. Исходя из определения следует, что действие этих факто ров можно определить с помощью неслучайной, циклической, как правило тригонометрической функции(рис. 4.3).

3. Циклические факторы, которые формируют периодиче­ские изменения уровней через большие интервалы времени, имеющие экономическую, социальную или астрофизическую

природу. Результат действия циклических факторов будем обо- шачать с помощью неслучайной периодической функцииI ели циклические факторы участвуют в формировании значе­ний уровней рядов динамики, то его модель будет выглядеть гак, как на рис. 4.4.

4. Случайные факторы,не поддающиеся регистрации и уче­ту. Случайные факторы обозначаются в виде случайной величи­ныГрафически влияние этих факторов можно представить так, как на рис. 4.5.

4.2.2. Аналитическая модель рядов динамики

Результат действия факторов 1—4 на значения уровней ряда динамики, изложенных в п. 4.2.1, можно представить в виде следующей аддитивной модели:

Иногда используется мультипликативная модель: Будем придерживаться смешанной формы записи:

Обозначив первое слагаемое из (4.11) в видеполучаем

при этом— неслучайная и случайная составляющие

рядов динамики соответственно.

4.2.3. Основные задачи уровней рядов динамики

Исходя из (4.10)—(4.12) можно сформулировать основные задачи анализа уровней рядов динамики:

1. определить, присутствует ли в разложении (4.12) неслу­чайная составляющая

2. выяснить, какие из факторовучаствуют в разложении (4.12);

3. для каждого из неслучайных факторов подобрать модель, описывающую его наиболее адекватно и точно;

4. получить оценки, «хорошо» описывающие действие слу­чайных факторов.

Замечание.В дальнейшем будем исследовать статистические прогнозы для коротких промежутков времени (до 10 лет). Кро­ме того, здесь рассматриваются «короткие» (по времени) ряды динамики. Поэтому рассмотрением циклических факторов мож­но пренебречь и считать, что они не оказывают существенного воздействия на рассматриваемые ряды динамики.

4.3. Неслучайная составляющая рядов динамики и точечный прогноз

4.3.1. Проверка гипотезы о наличии неслучайной составляющей

Этапу выявления и определения трендовой, сезонной и ци­клической составляющих предшествует ответ на принципиаль­ный вопрос: есть ли в рассматриваемом ряде динамики неслу­чайная составляющая? Ответ на него можно получить с помо­щью трех процедур. Проверка гипотезы о наличии неслучайной составляющей производится с доверительной вероятностью (на­дежностью)или с уровнем значимости

1. Проверка гипотезы о неизменности среднего значения уров­ней ряда динамики.Вначале из уровней рассматриваемого ряда строим вариационное распределение (записываем их значения в порядке неубывания):

Затем определяем величину медианы:

Далее наместе ставим знак

Еслито этому члену ряда не соответствует никакого

знака.

В результате получаем последовательность серий, состоящих из знаков + или —. Находим число v(n)серий и длину х(п)са­мой длинной из них.

Правило проверки гипотезы.Если хотя бы одно из нера­венств

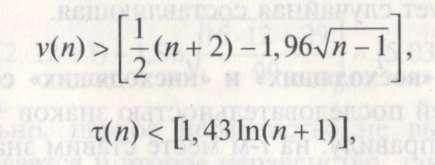
где [*] — целая часть числа,

окажется нарушенным, то с вероятностьюможно утверждать, что в исследуемом ряде динамики присут­ствует неслучайная составляющая.

ПРИМЕР 4.9.Проверить гипотезу о наличии в ряде динами­ки из примера 4.7 неслучайной составляющей.

Так как 5 > 0, первое неравенство выполнено. Но второе не­равенство не выполняется, 5 < 3. Из этого делаем с вероятно­стьювывод: в рассматриваемом ряде дина­мики присутствует случайная составляющая.

2. Критерий «восходящих» и «нисходящих» серий.Заменяем значения уровней последовательностью знаков + или — соглас­но следующему правилу: на /'-м месте ставим знак

Строим вариационный ряд: 0,99; 1,00; 1,04; 1, 06; 1,10; 1,14; 1,18; 1,20; 1, 20,1, 25; 1, 25; 1,35. Находим значение медианы (п = 12 — четное число):

Составляем последовательность знаков:

то этому члену не соответствует никакого знака. На последнем месте всегда ставится знак +. Получаем последовательность из серий знаков + и — с длинойсамой длинной из них.

Правило проверки гипотезы. Если хотя бы одно из нера- ненств

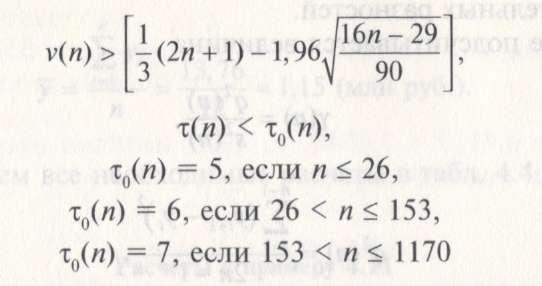
окажется нарушенным, то с вероятностьюможно утверждать, что в исследуемом ряде динамики присут­ствует неслучайная составляющая.

Следовательно, первое неравенство не выполнено. Нару­шенным оказывается и второе неравенство, так как

ПРИМЕР 4.10. Выяснить, имеется ли в ряде динамики из примера 4.7 неслучайная составляющая. Определяем знаки:

Итак, с вероятностьюутверждается, что в

исследуемом ряде динамики есть неслучайная составляющая.

3. Критерий квадратов последовательных разностей (критерий Аббе).Если есть основания полагать, что уровни ряда динамики относительно своего среднего значения подчинены нормально-

Для вероятностисо­

гласно таблице значений функции Лапласа, откуда

Так както факт наличия неслучайной со­

ставляющей подтверждается.

4.3.2. Функция тренда

Параметры уравнений функции тренда находят с помощью теории корреляции методом наименьших квадратов. Наиболее распространенными в экономике являются следующие регрес­сионные модели долговременных составляющих аналитической модели (4.1.3) ряда динамики (функции тренда).

1. Линейная модель

2. Степенная модель

*

3. Параболическая модель

4. Показательная модель

5. Смешанная модель

6. В некоторых случаях применяют более сложные виды за­висимостей между уи Г.

Значения параметров уравнений (4.13)—(4.19) регрессии на- \одят с помощью метода наименьших квадратов, решая систему нормальных уравнений.

Приведем системы нормальных уравнений для некоторых из перечисленных моделей:

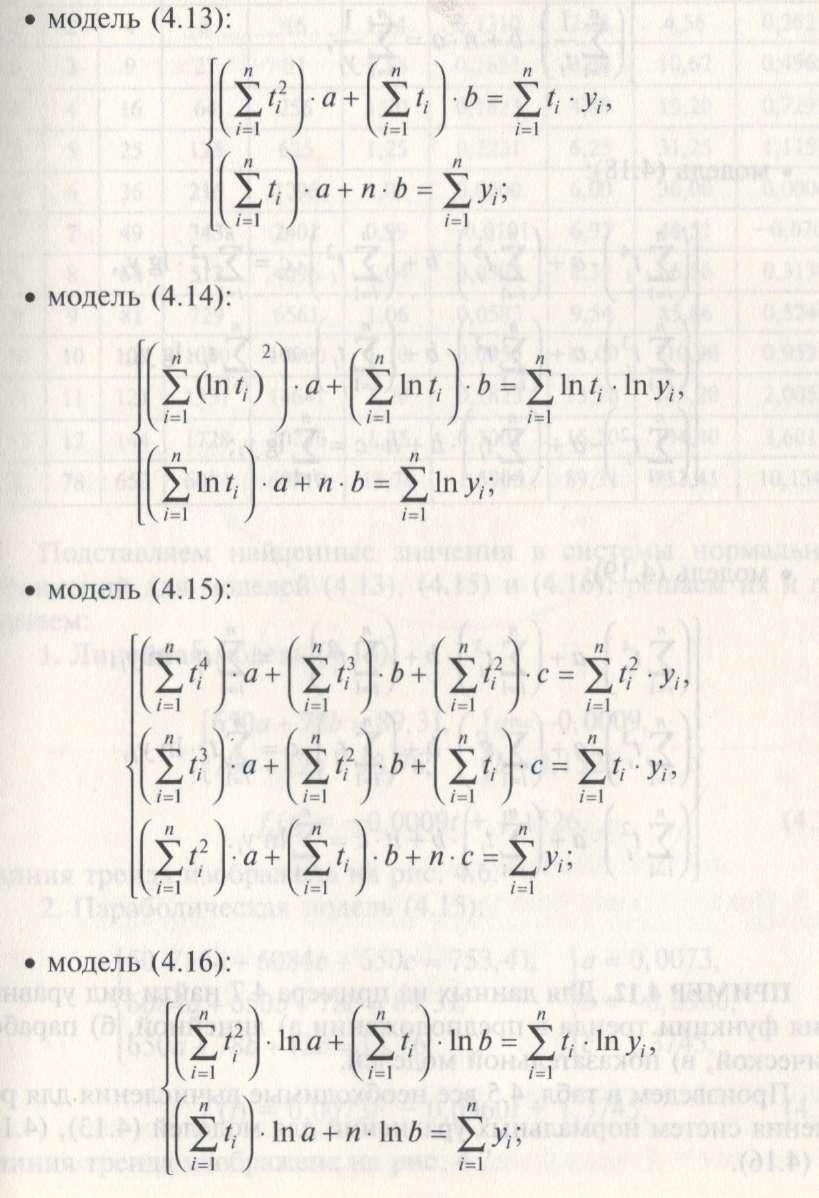
ПРИМЕР 4.12. Для данных из примера 4.7 найти вид уравне­ния функции тренда в предположении а) линейной, б) парабо­лической, в) показательной моделей.

Произведем в табл. 4.5 все необходимые вычисления для ре­шения систем нормальных уравнений для моделей (4.13), (4.15) и (4.16).

Таблица 4.5

Расчеты к примеру 4.12

/ по заданному значению у.Его вид устанавливается методом наименьших квадратов, решая систему нормальных уравнений. Например, для линейного случая параметрыиуравнения

находятся с помощью решения следующей системы:

4.3.3. Сезонная составляющая рядов динамики

Самым простым способом определения сезонных составля­ющих является индекс сезонности:

где— значение уровня ряда динамики, соответствующее интересую­щему нас интервалу времени (сезону); — среднее значение уровней ряда динамики.

ПРИМЕР 4.13.Вычислить индексы сезонности торгующей ор­ганизации по данным ее объемов продаж в 2007 г. (пример 4.7). Средний уровень ряда динамики (пример 4.11) составляет

Подсчитаем индекс сезонности по каждому из месяцев:

Видим, что максимальный объем продаж превышает средний уровень в январе, марте, апреле, мае, ноябре и декабреМаксимальный рост объема продаж наблюдается в декабре.

Данные о величинах индексов сезонности изображены на координатной плоскости в виде ломаной с вершинами в точках с координатами(рис. 4.9).

Подсчет индекса сезонности по одному году является нена­дежным, так как в этом случае велика вероятность влияния слу­чайных факторов. Поэтому на практике при расчете индекса сезонности пользуются месячными данными за клет (в основ­номВ этом случае индекс сезонностиравен

есть среднее значение средних уровней ряда динамики за клет.

мриэтом — среднее значение уровня (сезона) за клет,

ПРИМЕР 4.14.Рассчитать индексы сезонности торгующей орга­низации по данным ее объемов продаж 2005—2007 гг. (табл. 4.6).

Таблица 4.6

Исходные данные к примеру 4.14

Вычисления выполним в табл. 4.7.

Изобразим полученные значения индексов сезонности гра­фически (рис. 4.10). Для сравнения кривая, показывающая из­менения индексов сезонности за 2007 г., изображена пунктир­ной линией.

4.3.4. Неслучайная составляющая

С помощью индекса сезонности можно получить модель не­случайной составляющейс учетом сезонных составляющих:

где— значения индекса сезонности уровня ряда динамики в про­гнозируемый период временирассчитанного по функции тренда.

Одним из подходов моделирования неслучайной составляю­щей ряда динамики с учетом сезонного фактора является ее за­пись в виде уравнения Фурье:

где— степень точности гармоники тригонометрического ряда (чис­ло гармоник не должно превышать число наблюдений, т < и, на практике рассматривается не более четырех гармоник);

Например, приуравнение Фурье имеет вид

при= 2 когда= 3

Подсчет коэффициентовпроизводится методом наи­

меньших квадратов. Соответствующие расчетные формулы:

ПРИМЕР 4.15.По данным объемов продаж торгующей орга­низации в 2007 г. (пример 4.7) необходимо построить модель неслучайной составляющей в виде уравнения Фурье (число гар­моник взять равными 1, 2, и 3).

Для определения коэффициентовсоставляемрас­

четные таблицы (табл. 4.8—4.10).

» Таблица 4.8

Расчеты к примеру 4.15 при

Таблица 4.9

Расчеты к примеру 4.15 при

Таблица 4.10

Расчеты к примеру 4.15 при

Получаем:

Итак, в зависимости от числа гармоникуравнение Фурье имеет вид:

Строим чертеж (рис. 4.11).

4.3.5. Проверка точности модели

При статистическом прогнозировании по построенной мо­дели необходимо быть уверенным в ее точности.

Но вначале необходимо убедиться в статистической значи­мости (статистической существенности зависимости) эмпири­ческих данных. Если эмпирические данные значимы, то по­строенная по ним модель будет точна и соответственно точны­ми будут и полученные по ней прогнозы.

Вкачестве критерия проверки гипотезы о статистической существенности зависимости эмпирических данных рассмотрим /-критерий Стьюдента. Его использование основано на следую­щем утверждении.

Теорема.Если расчетное значение критерия /_на6лбольше кри­

тического

то это свидетельствует о статистическои существенности зави­симости Между признаками у и /. При этом

Замечание.Некоторые значенияприведены в табл. 2 Приложения С.

ПРИМЕР 4.16.С вероятностью 0,95 оценить существенность зависимости между признаками уи tиз примера 4.7.

Таблица 4.11

Расчеты к примеру 4.16

Произведем все необходимые вычисления в табл. 4.11.

Наблюдаемое значение критерия равно:

Поскольку 0,093 < 2,23, неравенство (4.26) не выполняется, заключаем с вероятностью 0,95: гипотеза о статистически суще­ственной зависимости между рассматриваемыми признаками отвергается.

Этот факт может быть объяснен малым числом выборочных данных (в примере число уровней

Эмпирические значения у,соответствующие значению t,мо­гут отличаться от теоретического значениярассчитанного по найденной модели неслучайной составляющей. Степень это­го отличия с помощью средней относительной ошибки или средней ошибки аппроксимации:

где — значение модели неслучайной составляющей, соответству­ющее дате

Принято считать, что еслито это свидетельствует

о высокой точности модели; если величинанаходится в пре­делах от 10 до 20%, то точность признается хорошей; точность считается удовлетворительной, если

Выбор модели является очень важной задачей. Правильность выбора обеспечивает более точней прогноз, что в итоге являет­ся целью любого статистического исследования. Очевидно, что более точной является та из модфлей, которой соответствует ми­нимум средней ошибки аппроксимации.

ПРИМЕР 4.17.По данным примера 4.7 необходимо: 1) опре­делить, какая из моделей неслучайной составляющей (функции тренда — линейная, параболическая или показательная с учетом индексов сезонности) наиболее точно описывает эмпирические

данные; 2) установить, какая из моделей неслучайной состав­ляющей ряда динамики, построенной с помощью уравнения Фурье, является наиболее точной.

Вначале для каждого значениянайдем зна­

чениефункции тренда. Затем скорректируем полученные результаты с помощью индексов сезонности согласно (4.24) (индексы сезонности для рассматриваемого ряда динамики вы­числены в примере 4.15), получаемНаконец, воспользовав­шись формулой (4.20), определяем значения средних ошибок аппроксимации для каждой из моделей функции тренда.

Все необходимые расчеты выполним в табл. 4.12.

Таблица 4.12

Расчеты к примеру 4.17

Получаем значения средних ошибок аппроксимации соглас­но (4.29):

Поскольку минимальное значение средней ошибки аппрок­симации соответствует (4.20), то утверждается, что наиболее точно описывает эмпирические данные следующая модель не­случайной составляющей:

Аналогичную работу проводим для уравнения Фурье (его вид для числа гармоникустановлен в при­

мере 4.15). Расчеты произведены в табл. 4.13. Имеем:

при

1) модель (4.20):

2) модель (4.21):

3) модель (4.22):

при при

Таблица 4.13

Расчеты к примеру 4.17

Сравнивая найденные величины средних ошибок аппрокси­мации, получаем:

Таким образом, наилучшей признается модель неслучайной составляющей с числом гармоник

4.3.6. Точечный прогноз

После того как установлен вид неслучайной составляющей, можно осуществить точечный прогнозуровня ряда динами­ки для данного значенияподстановкой интересующего нас значения времени в уравнение неслучайной составляющей.

ПРИМЕР 4.18.По данным примера 4.7 необходимо спрогно- шровать величину объема продаж торгующей организации на февраль 2008 г.

Для указанного периода величина

s⁼2,t— 14.

Подставляя соответствующее значение индекса сезонности (пример 4.13) в (4.30), получаем:

Л2.2008 = /(14) = /₂■ № = 0,99 • (-0,0009 • 14 + 1,1526) «

- 1,1332 (млн руб.). (4.32)

cosa₁₄=cos

3

Теперь произведем прогноз с помощью уравнения Фурье. Имеем:

./Iлi\⁷¹13л , я / = 14, ст₁₄= (14 -1) — = — = 2я + —,

j2K + ^j = cos^ = 0,866,

cos2a₁₄= cos2[ 2л + I = cos2 ■ ^ = cos— = 0,5,

cos3a,₄ = cos3^2n + ^-j = cos3 ■ ^ = cos-^ = 0,

= + = sin-^ = 0,5,

sin

2a₁₄ = sin2^2n+ = sin2 ~ = sin^- = 0,866, 3a,₄ = sin3^2n + ^j = sin3-^ = sin^ = 1.

sina,

sin

Тогда согласно (4.31)

>>02.2008 =Л14) = 1,1467 + 0,1141 0,866 + 0,0204 0,5 - - 0,0233 0,5 - 0,0548 0,866 + 0,0317 0 - 0,0583 1 = = 1,1382 (млн руб.). 149

Сравнивая средние ошибки аппроксимации обеих рассма триваемых моделей (0,2378% и 1,7842% соответственно), утверж даем, что прогноз (4.32) точный.