
- •Для студентов высших учебных заведений,
- •Введение
- •1. Общие указания
- •2. Правила оформления заданий и решения задач
- •Контрольные вопросы для подготовки к занятию
- •Число нейтронов в ядре
- •От массового числа a
- •Примеры решения задач
- •Энергия связи
- •Подставим числовые значения
- •Задачи для самостоятельного решения
- •Контрольные вопросы для подготовки к занятию
- •Краткие теоретические сведения и основные формулы
- •Контрольные вопросы для подготовки к занятию
- •Краткие теоретические сведения и основные формулы
- •Взаимодействие рентгеновского и -излучения с веществом
- •Эффект образования электронно-позитронных пар
- •Взаимодействие заряженных частиц с веществом
- •Примеры решения задач
- •Решение
- •Решение
- •Дано: Решение
- •Анализ решения задачи
- •Решение
- •Решение
- •Как объяснить этот результат?
- •Решение
- •Задачи для самостоятельного решения
- •Контрольные вопросы для подготовки к занятию
- •Краткие теоретические сведения и основные формулы
- •Примеры решения задач
- •Решение
- •Решение
- •Дано: Решение
- •Дано: Решение
- •Импульс тела связан с его кинетической энергией соотношением
- •Решение
- •Практический вывод
- •Решение
- •Задачи для самостоятельного решения
- •Занятие № 5
- •Для расчета реакторов на тепловых нейтронах большое значение имеет знание констант для нейтронов теплового спектра.
- •Величины стандартных сечений для некоторых нуклидов
- •Примеры решения задач
- •Контрольные вопросы для подготовки к занятию
- •Краткие теоретические сведения и основные формулы
- •Примеры решения задач
- •Решение
- •6.3. Энергетические спектры нейтронов
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Контрольные вопросы для подготовки к занятию
- •Диффузионные свойства важнейших замедлителей представлены в табл. 7.1.
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Занятие № 8 Теория деления ядра
- •Контрольные вопросы для подготовки к занятию
- •Краткие теоретические сведения и основные формулы
- •Распределение энергии деления ядра при делении его тепловыми нейтронами
- •Среднее число вторичных нейтронов, испускаемых на один акт деления
- •Элементарная теория деления Энергия деления. Параметр деления
- •Свойства осколков деления
- •Физические процессы отравления ядерного топлива
- •Энергетический спектр нейтронов деления
- •Мгновенные и запаздывающие нейтроны деления
- •Цепная реакция деления Практическое осуществление самоподдерживающейся цепной реакции деления
- •Определение коэффициента размножения в бесконечной размножающей среде. Формула четырех сомножителей
- •Примеры решения задач
- •Решение
- •Число ядер равно
- •Решение
- •Решение Тепловая энергия, выделившаяся за 1с работы реактора:
- •Следовательно, полный поток нейтрино:
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •По ядерной, нейтронной физике (задачи занятий № 6, № 7 и № 8 выполняют только студенты обучающиеся по специальности 7.090506)
- •Литература
- •Приложение
- •Масса нейтральных атомов
- •Периоды полураспада радиоактивных изотопов
- •Линейный коэффициент ослабления g-излучения в узком пучке
- •Экспериментальные данные по возрасту тепловых нейтронов
- •Массы и энергии покоя некоторых элементарных частиц
- •Ирина Васильевна Вах Геннадий Яковлевич Мерзликин
- •По ядерной и нейтронной физике
Примеры решения задач
Задача
1.
Вычислить
дефект массы и энергию связи ядра
![]() .
.
Дано: Решение
![]()
 Дефект
массы ядра равен
Дефект
массы ядра равен
А = 11 т = Z mp + (A – Z) mn - Mядра. (1)
Z = 5 Выразим массу ядра через массу атома и массу всех
N = A – Z = 6 электронов:
![]() а.е.м.
Мат
= Мяд
+ Z
me;
а.е.м.
Мат
= Мяд
+ Z
me;
тп
= 1,00867 а.е.м. Мяд
=
Мат
– Z
me;
(тр
+ те)
=
![]() .
.
тв = 11,00930 а.е.м. Тогда
т
- ? Е
- ?
![]() ;
;
![]() .
(2)
.
(2)
Формула (2) является расчетной формулой дефекта массы. По формуле (1) определить дефект массы нельзя, так как в существующих таблицах даны не массы ядер, а массы нейтральных атомов (см. табл. 1 приложения).
После подстановки численных значений, получим:
т = 5 . 1,00783 + 6 . 1,00867 – 11,00930 = 0,08186 а.е.м.
Энергия связи
Е = т с2,
или Е = 0,08186 . 931,5 = 76 МэВ.
Ответ: т = 0,08186 а.е.м.; Е = 76 МэВ.
Задача
2.
Определить энергию, необходимую для
отделения одного нейтрона от ядра
![]() .
.
Д ано:Решение
ано:Решение
![]() Энергия
отделения от ядра одного нейтрона
Энергия
отделения от ядра одного нейтрона
![]() а.е.м
численно равна энергии связи нейтрона
с
а.е.м
численно равна энергии связи нейтрона
с
![]() а.е.м.
ядром.
а.е.м.
ядром.
![]() а.е.м
Еп
= т
с2;
а.е.м
Еп
= т
с2;
 Еп
- ? т
= тп
+
Еп
- ? т
= тп
+
![]() ,
,
Подставим численные значения масс, взятые из табл. 1 приложения:
т = 1,00867 + 21,99440 – 22,98977 = 0,01334 а.е.м.;
Еп = т . с2 = 931,5 . 0,01334 = 12,4 МэВ.
Ответ: Еп = 12,4 МэВ.
Задача
3.
Какую наименьшую энергию нужно затратить,
чтобы отделить один протон от ядра
![]() ?
?
 Дано:
Решение
Дано:
Решение
![]() В
результате отделения одного протона
от ядра
В
результате отделения одного протона
от ядра
![]() а.е.м.
а.е.м.
![]() получается новое ядро
получается новое ядро![]() и протон.
и протон.
тр = 1,00728 а.е.м. Изменение массы
![]() а.е.м.
а.е.м.
![]()
Ер
- ? Энергия связи протона
в ядре![]()
![]() .
.
Подставим числовые значения
![]() МэВ.
МэВ.
Ответ: Ер = 7,04 МэВ.
Задача
4.
Определить удельную энергию связи ядра
![]() .
.
 Дано:
Решение
Дано:
Решение
МU = 238,05076 а.е.м. Удельной энергией связи называется средняя
А = 238 энергия связи, приходящаяся на один нуклон в ядре,
Z
= 92 т. е.
![]() ;
;
A – Z
=
146
– Z
=
146
![]() .
.
- ?
или
![]()
![]()
![]()
Ответ:
![]()
Задача
5.
Какую наименьшую энергию нужно затратить,
чтобы разделить ядро
![]() на
две одинаковые части.
на
две одинаковые части.
Д ано:
Решение
ано:
Решение
![]() В
результате деления ядра
В
результате деления ядра
![]() на две одинаковые
на две одинаковые
![]() а.е.м.
части получается два ядра дейтерия
а.е.м.
части получается два ядра дейтерия
![]() .
Сумма масс
.
Сумма масс
![]() а.е.м.
образовавшихся ядер больше массы ядра
а.е.м.
образовавшихся ядер больше массы ядра
![]() :
:
 Е
- ?
Е
- ?
![]() ;
;
![]() МэВ.
МэВ.
Ответ: Е = 23,85 МэВ.
Задача
6.
Сколько энергии выделится при образовании
1 г
![]() из протонов и нейтронов?
из протонов и нейтронов?
 Дано:
Решение
Дано:
Решение
М![]() = 4,00260 а.е.м. При образовании одного
ядра
= 4,00260 а.е.м. При образовании одного
ядра
![]() из протонов и
из протонов и
![]() а.е.м.
нейтронов выделится энергия, равная
численно
а.е.м.
нейтронов выделится энергия, равная
численно
тп
= 1,00867 а.е.м. энергии связи ядра
![]() .
.
Q - ? Определим энергию
связи ядра:
- ? Определим энергию
связи ядра:
![]() ;
;
![]() МэВ.
МэВ.
В
1 г
![]() содержитсяN
атомов (ядер):
содержитсяN
атомов (ядер):
![]() ,
,
где
- молярная масса
![]() :
:![]()
4 .
10-3
кг/моль;
NA
– число Авогадро.
4 .
10-3
кг/моль;
NA
– число Авогадро.
Тогда полная энергия Q, выделившаяся при образовании 1 г гелия, равна
![]() МэВ;
МэВ;
1 МэВ = 1,6 . 10-13 Дж.
Q = 26 . 1010 Дж.
Ответ:
При синтезе 1 г
![]() выделяется энергия
выделяется энергия
Q
= 42 .
1023
МэВ=26![]() Дж.
Дж.
Задача
7.
Энергия связи ядра
![]() равна 139,8 МэВ; ядра
равна 139,8 МэВ; ядра![]() МэВ. Определить минимальную энергию,
необходимую для отделения одного протона
от ядра
МэВ. Определить минимальную энергию,
необходимую для отделения одного протона
от ядра![]() .
.
Д ано:Решение
ано:Решение
Е1 = 139,8 МэВ Схема отделения протона
Е2
= 147,8 МэВ
![]()
А1
= 18 Энергия связи протона в
ядре
![]() :
:
А2
= 19
![]() (1)
(1)
Z1
= 8 Энергия связи ядра
![]() :
:![]() ;
;
Z2
= 9 Энергия связи ядра
![]() :
:![]() ;
;
N1
= N2
= 10 Вычтем Е1
из формулы
![]() .
Получим
.
Получим
 Ер
- ?
Ер
- ?
![]() .
(2)
.
(2)
Сравним
выражение (2) с выражением (1):
![]() .
.
Вычисляя, получим: Ер = 147,8 – 139,8 = 8 МэВ.
Ответ: Ер = 8 МэВ.
Задача
8.
Какую наименьшую энергию нужно затратить,
чтобы разделить на отдельные нуклоны
изобарные ядра
![]() и
и![]() ?
?
Д ано:Решение
ано:Решение
![]() Е1
= 931,5 .
(3 .
1,00783
+ 4 .
1,00867
– 7,01601) =
Е1
= 931,5 .
(3 .
1,00783
+ 4 .
1,00867
– 7,01601) =
А = 7 А = 7 = 931,5 . 0,4216 = 39,2 МэВ;
Z = 3 Z = 4 Е2 = 931,5 . (4 . 1,00783 + 3 . 1,00867 – 7,01693) =
N = 4 N = 3 = 931,5 . 0,04040 = 37,6 МэВ.
![]() а.е.м.
а.е.м.
![]() а.е.м.
а.е.м.
 Е1
- ? Е2
- ?
Е1
- ? Е2
- ?
Ответ: ЕLi = 39,2 МэВ; ЕВе = 37,6 МэВ.
Задача
9.
Найти энергию связи ядер
![]() и
и![]() .
Какое из этих ядер наиболее устойчиво?
.
Какое из этих ядер наиболее устойчиво?
Д ано:
Решение
ано:
Решение
![]()
![]() МэВ
=
МэВ
=

![]() =
(1,00783 + 2 .
1,00867
–
=
(1,00783 + 2 .
1,00867
–
Е1 - ? – 3,01605) . 931,5 МэВ = 8,5 МэВ;
Е2 - ? Е2 = (1,00783 . 2 + 1,00867 – 3,01603) . 931,5 МэВ =
= 6,8 МэВ;
![]()
![]()
![]()
Оба
ядра содержат одинаковое количество
нуклонов, но ядро
![]() более устойчиво, чем ядро
более устойчиво, чем ядро![]() ,
так как в состав
,
так как в состав![]() (в отличие от
(в отличие от![]() )
входит 2 протона, между которыми существуют
силы кулоновского отталкивания, что
уменьшает энергию связи ядра.
)
входит 2 протона, между которыми существуют
силы кулоновского отталкивания, что
уменьшает энергию связи ядра.
Задача
10.
Используя формулу Вайцзеккера, определить
массу ядра тяжелого водорода
![]() .
.
Д ано:Решение
ано:Решение
тр = 1,00728 а.е.м. Энергия связи ядра
тп
= 1,00867 а.е.м.
![]() .
.
= 15,75 МэВ Найдем массу ядра
=
17,8 МэВ
![]() .
.
= 0,71 МэВ Запишем полуэмпирическую формулу Вайцзеккера,
= 94,8 МэВ позволяющую определить энергию связи ядра:
 =
34 МэВ
=
34 МэВ
тя - ?
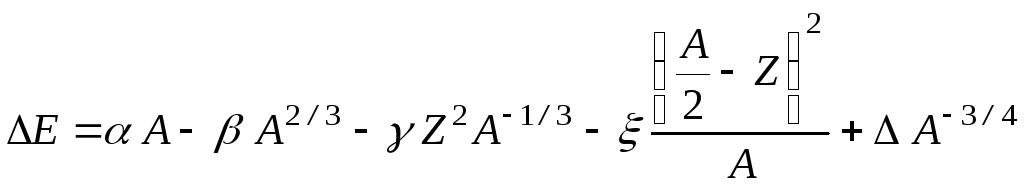 ,
,
где А – массовое число; Z – зарядовое число; , , , , - поправочные коэффициенты, с помощью которых учитываются силы кулоновского отталкивания протонов, энергия поверхностного натяжения ядра-капли, соотношение между числом протонов и нейтронов в ядре, четность или нечетность ядер. Масса ядра с учетом формулы Вайцзеккера для тяжелого водорода:
![]()
![]() .
.
Ядро нечетно-нечетное.
![]() .
.
Ответ:
![]() а.е.м.
а.е.м.
