
- •Для студентов высших учебных заведений,
- •Введение
- •1. Общие указания
- •2. Правила оформления заданий и решения задач
- •Контрольные вопросы для подготовки к занятию
- •Число нейтронов в ядре
- •От массового числа a
- •Примеры решения задач
- •Энергия связи
- •Подставим числовые значения
- •Задачи для самостоятельного решения
- •Контрольные вопросы для подготовки к занятию
- •Краткие теоретические сведения и основные формулы
- •Контрольные вопросы для подготовки к занятию
- •Краткие теоретические сведения и основные формулы
- •Взаимодействие рентгеновского и -излучения с веществом
- •Эффект образования электронно-позитронных пар
- •Взаимодействие заряженных частиц с веществом
- •Примеры решения задач
- •Решение
- •Решение
- •Дано: Решение
- •Анализ решения задачи
- •Решение
- •Решение
- •Как объяснить этот результат?
- •Решение
- •Задачи для самостоятельного решения
- •Контрольные вопросы для подготовки к занятию
- •Краткие теоретические сведения и основные формулы
- •Примеры решения задач
- •Решение
- •Решение
- •Дано: Решение
- •Дано: Решение
- •Импульс тела связан с его кинетической энергией соотношением
- •Решение
- •Практический вывод
- •Решение
- •Задачи для самостоятельного решения
- •Занятие № 5
- •Для расчета реакторов на тепловых нейтронах большое значение имеет знание констант для нейтронов теплового спектра.
- •Величины стандартных сечений для некоторых нуклидов
- •Примеры решения задач
- •Контрольные вопросы для подготовки к занятию
- •Краткие теоретические сведения и основные формулы
- •Примеры решения задач
- •Решение
- •6.3. Энергетические спектры нейтронов
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Контрольные вопросы для подготовки к занятию
- •Диффузионные свойства важнейших замедлителей представлены в табл. 7.1.
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Занятие № 8 Теория деления ядра
- •Контрольные вопросы для подготовки к занятию
- •Краткие теоретические сведения и основные формулы
- •Распределение энергии деления ядра при делении его тепловыми нейтронами
- •Среднее число вторичных нейтронов, испускаемых на один акт деления
- •Элементарная теория деления Энергия деления. Параметр деления
- •Свойства осколков деления
- •Физические процессы отравления ядерного топлива
- •Энергетический спектр нейтронов деления
- •Мгновенные и запаздывающие нейтроны деления
- •Цепная реакция деления Практическое осуществление самоподдерживающейся цепной реакции деления
- •Определение коэффициента размножения в бесконечной размножающей среде. Формула четырех сомножителей
- •Примеры решения задач
- •Решение
- •Число ядер равно
- •Решение
- •Решение Тепловая энергия, выделившаяся за 1с работы реактора:
- •Следовательно, полный поток нейтрино:
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •По ядерной, нейтронной физике (задачи занятий № 6, № 7 и № 8 выполняют только студенты обучающиеся по специальности 7.090506)
- •Литература
- •Приложение
- •Масса нейтральных атомов
- •Периоды полураспада радиоактивных изотопов
- •Линейный коэффициент ослабления g-излучения в узком пучке
- •Экспериментальные данные по возрасту тепловых нейтронов
- •Массы и энергии покоя некоторых элементарных частиц
- •Ирина Васильевна Вах Геннадий Яковлевич Мерзликин
- •По ядерной и нейтронной физике
Цепная реакция деления Практическое осуществление самоподдерживающейся цепной реакции деления
Возможность цепной реакции деления состоит в том, что нейтроны деления каждого следующего поколения сами способны вызвать реакцию деления других делящихся ядер. Если в результате деления испускаются ν нейтронов на один акт деления, и все они вступят в реакцию деления, то вновь возникнет ν2 новых нейтронов, которые дадут ν3 нейтронов и т.д.
Вывод 1. Необходимое (но не достаточное) условие самоподдерживающейся цепной реакции деления – возникновение в результате деления ядра одного (или более) нейтронов.
В качестве ядерного топлива естественно выбрать природный уран. Он состоит в основном из двух изотопов:
99,28
% -
![]() U;
0,71 % -
U;
0,71 % -![]() U.
U.
![]() U
делится быстрыми нейтронами (с энергиями
более 1,1 МэВ), значит, и нейтронами деления
(их средняя энергия 2 МэВ). Но кроме
реакции деления (n, f) при взаимодействии
нейтрона с ядром возможны процессы
радиационного захвата (n,
U
делится быстрыми нейтронами (с энергиями
более 1,1 МэВ), значит, и нейтронами деления
(их средняя энергия 2 МэВ). Но кроме
реакции деления (n, f) при взаимодействии
нейтрона с ядром возможны процессы
радиационного захвата (n,
![]() )
и упругого (n, n) и неупругого (n, n
)
и упругого (n, n) и неупругого (n, n![]() )
рассеяния (главным образом, неупругого,
т.к. энергия нейтронов велика). При этом
сечение реакции деления238U
быстрыми нейтронами (с энергиями от 2
до 6 МэВ) равно
)
рассеяния (главным образом, неупругого,
т.к. энергия нейтронов велика). При этом
сечение реакции деления238U
быстрыми нейтронами (с энергиями от 2
до 6 МэВ) равно
![]() ,
а полное сечение взаимодействий быстрого
нейтрона с ядром238U
,
а полное сечение взаимодействий быстрого
нейтрона с ядром238U
![]() барн. То есть:
барн. То есть:

Вывод 2. Вероятность реакций (n, ) и (n, n) для 238U на быстрых нейтронах (Е = 26 МэВ) примерно в 4 раза больше, чем вероятность деления.
Радиационный захват нейтронов приводит к бесполезной их потере для реакции деления. Неупругое рассеяние приводит к потере большей части энергии нейтрона, т.е. энергия становится ниже порога деления 238U.
Пусть в результате деления образовалось в среднем приблизительно 2,5 нейтронов на одно деление.
Из
них 4/5, то есть 2 нейтрона, будут потеряны
для реакции деления на 238U
из-за реакции рассеяния (n, n![]() )
и радиационного захвата (n,
)
и радиационного захвата (n,![]() ).
Остается приблизительно 0,5 нейтрона.
Этого мало для поддержания цепной
реакции деления (см. вывод 1).
).
Остается приблизительно 0,5 нейтрона.
Этого мало для поддержания цепной
реакции деления (см. вывод 1).
Вывод 3. Самоподдерживающаяся цепная реакция деления на ядрах 238U не может быть осуществлена.
Нейтроны, испытавшие неупругое рассеяние, потеряны для деления 238U, но совершенно не потеряны для деления 235U, т.к. 235U делится как быстрыми, так и тепловыми нейтронами. Поэтому можно попытаться организовать цепную реакцию деления с участием чистого 235U как на быстрых, так и на тепловых нейтронах.
Сечение деления 235U тепловыми нейтронами (с E = 0,025 эВ) f = =582,3 барна, сечение поглощения - a = 680,9 барн. Таким образом, вероятность деления 235U тепловыми нейтронами соизмерима с вероятностью их поглощения, хотя ядер-поглотителей в природном уране больше, чем ядер, способных к делению на тепловых нейтронах.
Вывод 4. Имеется принципиальная возможность провести самоподдерживающуюся цепную реакцию деления на 235U.
Нейтрон деления имеет очень большую вероятность быть захваченным без деления ядром 238U. На рис. 8.10 показан характер зависимости сечения поглощения 238U от энергии нейтрона.

Рис. 8.10. Зависимость величин полных сечений (1),
сечений деления (4) и радиационного захвата (3)
для 238U и величин сечения деления 235U (2)
от энергии нейтронов
Из графика видно, что при энергии от 6 до 600 эВ сечение радиационного захвата 238U очень велико, и захват нейтронов в этом диапазоне энергий имеет резонансный характер. Следует отметить, что резонансная область энергий приходится на период нахождения нейтрона в процессе медленного снижения энергии. Поэтому при замедлении на тяжелых ядрах время пребывания нейтрона при энергиях резонансного интервала велико, что еще больше увеличивает вероятность резонансного захвата нейтронов данных энергий ядрами 238U.
Вывод 5. Создание благоприятных условий для самоподдерживающейся цепной реакции деления возможно: 1)путем увеличения доли ядер 235U в уране, т.е. обогащения природного урана; 2)путем применения замедлителя.
С повышением обогащения вероятность резонансного поглощения в 238U уменьшается, а вероятность поглощения нейтрона ядрами 235U с последующим делением - увеличивается.
Применение замедлителя является радикальным средством уменьшения вероятности резонансного поглощения в 238U, так как замедляющийся нейтрон, мигрирующий в смеси топлива и замедлителя, может пройти область резонансных энергий, взаимодействуя с замедлителем, а не с ураном.
Применение замедлителя дает и другой положительный эффект: сечение деления изотопов 235U, 233U, 239Pu растет с уменьшением энергии нейтронов в большей степени, чем их сечение захвата (рис. 8.10).
При использовании обогащенного топлива легче создать условия для самоподдерживающейся цепной реакции деления на тепловых нейтронах, чем на быстрых. В качестве замедлителя применяют легкие вещества, обладающие в интервале энергий замедления малым сечением поглощения, но большим сечением рассеяния. Например, вода, графит, тяжелая вода, бериллий и др.
На
современном уровне развития
реакторов-размножителей, в которых
получают 233U
и 239Pu,
уже созданы реакторы на быстрых нейтронах,
работающие без замедлителя. Топливной
композицией в них является UO2
с 20![]() 25-процентным
обогащением по235U.
25-процентным
обогащением по235U.
Для того чтобы процесс взаимодействия с замедлителем был более вероятным, чем с 238U, реактор на тепловых нейтронах имеет особое расположение топлива относительно замедлителя. В таком гетерогенном реакторе область замедления отделена от места концентрации топлива, где нейтрон может с большой вероятностью поглотиться. Выйдя из блока с топливом, быстрый нейтрон проходит довольно большой путь в замедлителе, и только после этого снова попадает в блок с топливом (рис. 8.11).
Неуправляемая цепная реакция деления реализуется в атомной бомбе, созданной впервые в 1945 году. Трудности реализации этого процесса были связаны на первых этапах с необходимостью получения достаточного количества чистого 235U или другого делящегося нуклида - 239Pu.
Управляемая цепная реакция деления впервые была осуществлена в 1942 г. под руководством Э. Ферми в Чикаго.
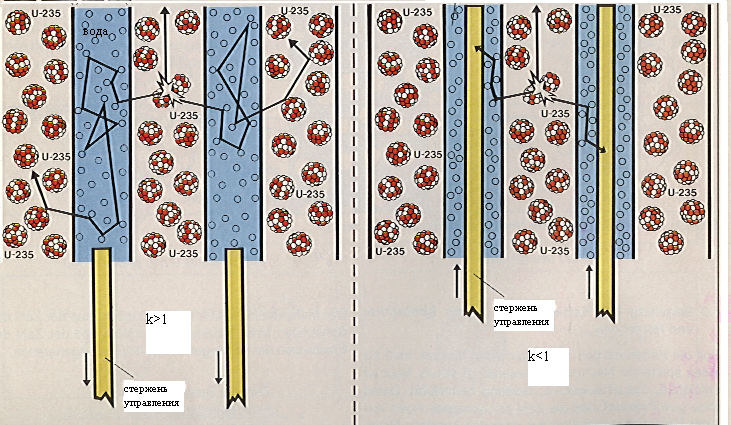
Рис. 8.11. Принципиальная схема гетерогенного реактора
Коэффициент размножения в бесконечной
размножающей среде
Для оценки условий поддержания цепной реакции деления вводят коэффициент размножения k, определяемый как отношение средних по объёму активной зоны плотностей тепловых нейтронов данного и непосредственно предшествующего ему поколений.
Если
размножающая среда будет иметь бесконечно
большие размеры, то утечки нейтронов
не будет. Для бесконечной среды:

При k = 1 плотность нейтронов в каждом последующем поколении остается неизменной, реакция в такой среде идет с постоянной скоростью. Если k > 1, плотность нейтронов в среде, а, следовательно, и скорость (удельная частота) деления в каждом ее см3 монотонно растет.
При k < 1 реакция с течением времени будет затухать. Коэффициент размножения нейтронов в бесконечной среде определяет возможность получения цепной самоподдерживающейся реакции деления в «активной зоне» бесконечных размеров. Коэффициент размножения такой системы всегда больше, чем в ограниченной по размерам, но такой же по составу. Значение k может быть использовано для качественной оценки осуществимости самоподдерживающейся ресамоподдерживающейся реакции деления в размножающей среде конечных размеров. Критическое состояние в размножающей среде конечных размеров достижимо только при k > 1. Во всех остальных случаях дальнейшие работы по проектированию реактора не имеют смысла, т.к. не могут дать положительного результата. Поэтому физический расчёт реактора начинают с вычисления k, чтобы сразу отбросить те варианты компоновки и состава активной зоны, в которых k 1.
