
- •Министерство аграрной политики украины
- •Издание рассмотрено и рекомендовано к печати на заседании кафедры физико-математических дисциплин (протокол № 2 от 9 октября 2007г.);
- •Содержание
- •1. Линейная алгебра
- •1.1. Системы линейных уравнений
- •1.2. Метод обратной матрицы
- •1.3. Метод Крамера
- •1.4. Метод Гаусса
- •1.5. Вопросы для самоконтроля
- •2. Аналитическая геометрия на плоскости
- •2.1. Линии первого порядка
- •2.2. Линии второго порядка Окружность
- •Гипербола
- •Парабола
- •2.3. Вопросы для самоконтроля
- •3. Векторная алгебра
- •3.1. Основные определения и понятия
- •3.2. Скалярное произведение векторов
- •3.3. Векторное произведение векторов
- •3.4. Смешанное произведение векторов
- •3.5. Вопросы для самоконтроля
- •4. Аналитическая геометрия в пространстве
- •4.1. Плоскость в пространстве
- •4.2. Прямая в пространстве
- •4.3. Прямая и плоскость в пространстве
- •4.4. Вопросы для самоконтроля
- •Литература
- •Индивидуальные задания к расчётно-графической работе Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Для выполнения ргр
- •211 Группа
- •212 Группа
- •213 Группа
- •214 Группа
- •215 Группа
- •311 Группа
- •312 Группа
- •313 Группа
- •314 Группа
- •315 Группа
- •316 Группа
- •1111 Группа
- •1112 Группа
- •1211 Группа
- •1212 Группа
- •1311 Группа
- •1312 Группа
- •1313 Группа
- •1511 Группа
- •1512 Группа
3. Векторная алгебра
3.1. Основные определения и понятия
Вектором называется направленный отрезок.
Вектор, начало и конец которого совпадают, называется нулевым.
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.
Векторы называются равными, если они коллинеарны, имеют одинаковые длины и одинаковые направления.
Для каждого вектора точка приложения может быть выбрана произвольно. Поэтому не различают равных векторов, получающихся друг из друга параллельным переносом. В этом смысле векторы называют свободными.
Длина вектора (при
заданном масштабе) называется его
модулем. Модуль нулевого вектора равен
нулю. Модуль вектора ![]() обозначают
|
обозначают
|![]() |.
|.
Проекции вектора
на оси координат определяют его как
свободный вектор (с точностью до положения
в пространстве). Проекции ах,
ау,
аz
вектора ![]() на координатные оси называют его
декартовыми
координатами.
на координатные оси называют его
декартовыми
координатами.
Вектор ![]() с координатами ах,
ау,
аz
записывается в виде:
с координатами ах,
ау,
аz
записывается в виде:
![]() или
или
![]() .
.
Если даны две
точки А(х1;
у1;
z1)
и В(х2;
у2;
z2),
то координаты
вектора
![]() ( проекции вектора на координатные оси)
определяются формулами:
( проекции вектора на координатные оси)
определяются формулами:
ах = х2 – х1; ау = y2 – y1; аz = z2 – z1.
(Для получения координат вектора нужно от координат его конца отнять соответствующие координаты его начала.)
Модуль вектора
![]() (его длина) вычисляется по формуле:
(его длина) вычисляется по формуле:
![]() .
.
Если модуль
вектора
![]() равен единице,
равен единице,![]() = 1,
то вектор
= 1,
то вектор
![]() называется
единичным.
называется
единичным.
Единичный вектор,
имеющий одинаковое направление с данным
вектором
![]() ,
называетсяортом
вектора
,
называетсяортом
вектора
![]() и обозначается
и обозначается![]() .
.
Проекция
вектора
![]() на осьu
выражается формулой:
на осьu
выражается формулой:
при![]() ,
,
где
– угол наклона вектора
![]() к
осии.
к
осии.
Если ,
,
– углы, которые составляет вектор
![]() с координатными осями, то величины соs,
cos,
cos
называются направляющими
косинусами
вектора
с координатными осями, то величины соs,
cos,
cos
называются направляющими
косинусами
вектора
![]() (рис.
16).
(рис.
16).
Из формулы проекции вектора на ось следуют соотношения:
ах
=
![]() .
.
Можно определить любой из углов , зная два других, по формуле:
cоs2 + cos2 + cos2 = 1.

Рис. 16
К линейным операциям над векторами относят сложение векторов и умножение вектора на число.
Пусть заданы
векторы
![]() и
и![]() .
.
Тогда имеют место следующие соотношения:
![]() ;
;
![]() .
.
При умножении
вектора
![]() на число
его координаты умножаются на это число:
на число
его координаты умножаются на это число:
![]() .
.
Признаком
коллинеарности
двух векторов
![]() и
и![]() является пропорциональность их координат:
является пропорциональность их координат:
![]() .
.
Тройка векторов
![]() называется координатнымбазисом,
если эти векторы удовлетворяют следующим
условиям:
называется координатнымбазисом,
если эти векторы удовлетворяют следующим
условиям:
вектор
 лежит на осиОх;
вектор
лежит на осиОх;
вектор
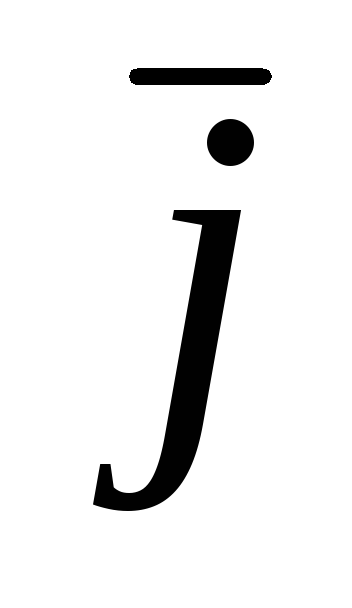 – на осиОу;
вектор
– на осиОу;
вектор
 – на осиОz;
– на осиОz;каждый из векторов
 направлен на своей оси в положительную
сторону;
направлен на своей оси в положительную
сторону;векторы
 –
единичные;
–
единичные; .
.
Произвольный
вектор
![]() может быть
разложен по базису
может быть
разложен по базису
![]() :
:
![]() .
.
Коэффициенты этого
разложения являются координатами
вектора
![]() :ах,
ау,
аz
есть проекции вектора
:ах,
ау,
аz
есть проекции вектора
![]() на координатные оси.
на координатные оси.
3.2. Скалярное произведение векторов
Скалярным
произведением
двух векторов
![]() и
и![]() называется число, равное произведению
модулей этих векторов на косинус угла
между ними:
называется число, равное произведению
модулей этих векторов на косинус угла
между ними:
![]() ,
,
где
– угол между векторами
![]() и
и![]() .
.
Скалярное
произведение векторов
![]() и
и![]() можно рассматривать как произведение
двух чисел, из которых одно есть модуль
вектора
можно рассматривать как произведение
двух чисел, из которых одно есть модуль
вектора![]() другие – проекция вектора
другие – проекция вектора![]() на ось вектора
на ось вектора![]() :
:
![]() .
.
Аналогично имеет место формула:
![]() .
.
Скалярное
произведение
![]() называется скалярным квадратом вектора
называется скалярным квадратом вектора![]() и обозначается символом
и обозначается символом![]() .
Скалярный квадрат вектора равен квадрату
его модуля:
.
Скалярный квадрат вектора равен квадрату
его модуля:![]() .
.
Если
векторы
![]() и
и![]() заданы своими координатами,
заданы своими координатами,![]() ,
,![]() ,
тоскалярное
произведение
,
тоскалярное
произведение
![]()
![]() равно сумме попарных произведений
соответствующих координат этих векторов:
равно сумме попарных произведений
соответствующих координат этих векторов:
![]()
![]() =
ах
bx
+
аy
by
+ аz
bz.
=
ах
bx
+
аy
by
+ аz
bz.
Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю скалярного произведения:
![]()
![]() =
ахbx
+ аyby
+ аzbz
= 0.
=
ахbx
+ аyby
+ аzbz
= 0.
Угол
между векторами
![]() и
и![]() определяется соотношением:
определяется соотношением:
![]() ;
;
![]() .
.
